线性SVM决策过程的可视化

Posted 2023-04-24 Thank CAT

线性 SVM 决策过程的可视化

导入模块

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np

实例化数据集，可视化数据集

x, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.5)
# plt.scatter(x[:, 0], x[:, 1], c=y, cmap="rainbow")
# plt.xticks([])
# plt.yticks([])

画决策边界

# 首先要有散点图
plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
# 获取当前的子图，如果不存在，则创建新的子图
ax = plt.gca()

# 获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()  # (-0.46507821433712176, 3.1616962549275827)
ylim = ax.get_ylim()  # (-0.22771027454251097, 5.541407658378895)

# 在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0], xlim[1], 30)  # shape(30,)
axisy = np.linspace(ylim[0], ylim[1], 30)  # shape(30,)

# 将axis（x, y）转换成二维数组
axisx, axisy = np.meshgrid(axisx, axisy)  # axisx, axisy = shape((30, 30)

# 将axisx, axisy 组成 900 * 2 的数组
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T  # shape(900, 2)

# 展示xy画出的网格图
# plt.scatter(xy[:, 0], xy[:, 1], s=1, c="grey", alpha=0.3)

​

​

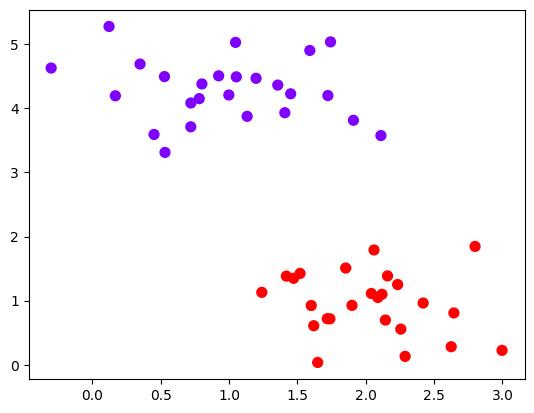
建模，计算决策边界并找出网格上每个点到决策边界的距离

# 建模，通过fit计算出对应的决策边界
clf = SVC(kernel="linear").fit(x, y)

# 重要接口decision_function，返回每个输入的样本所对应的到决策边界的距离
z = clf.decision_function(xy).reshape(axisx.shape)  # shape(30, 30)

plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
ax = plt.gca()

# 画决策边界和平行于决策边界的超平面
ax.contour(
    axisx,
    axisy,
    z,
    colors="k",
    levels=[-1, 0, 1],
    linestyles=["--", "-", "--"],
    alpha=0.5,
)

# 设置xyk刻度
ax.set_xlim(xlim)
ax.set_ylim(ylim)

(-0.22771027454251097, 5.541407658378895)

​

​

将绘图过程包装成函数

# 将上述过程包装成函数：
def plot_svc_decision_function(model: SVC, ax=None):
    """画出线性数据中策边界和平行于决策边界的超平面

    Args:
        model (SVC): 模型
        ax (_type_, optional): 子图. Defaults to None.
    """
    if ax is None:
        ax = plt.gca()  # 获取子图或新建子图
    xlim = ax.get_xlim()  # 获取子图x轴最大值和最小值
    ylim = ax.get_ylim()  # 获取子图y轴最大值和最小值

    # 在最大值和最小值之间形成30个规律的数据
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)

    # 将x,y转换成x^2, y^2的二维数组
    Y, X = np.meshgrid(y, x)
    # 组成 xy * 2 的数组
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    # 获取每个输入的样本所对应的到决策边界的距离
    P = model.decision_function(xy).reshape(X.shape)

    # 画图
    ax.contour(
        X, Y, P, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"]
    )
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

clf = SVC(kernel="linear").fit(x, y)
plt.scatter(x[:, 0], x[:, 1], s=50, cmap="rainbow", c=y)
plot_svc_decision_function(clf)

​

​

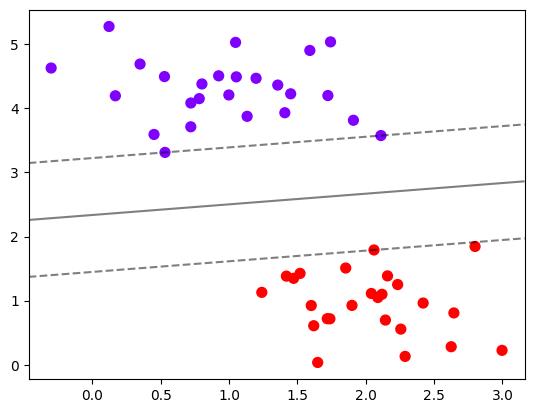
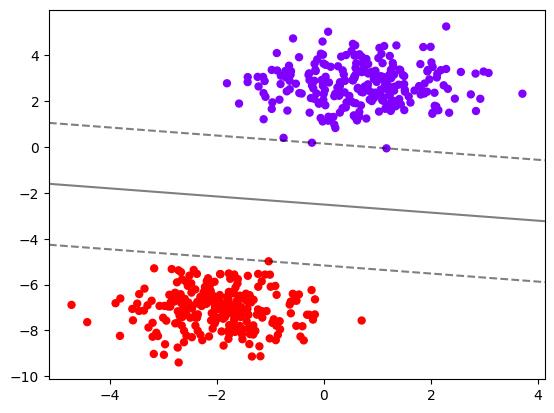
# 测试
x1, y1 = make_blobs(n_samples=500, centers=2, cluster_std=0.9)
clf1 = SVC(kernel="linear").fit(x1, y1)
plt.scatter(x1[:, 0], x1[:, 1], c=y1, s=25, cmap="rainbow")
plot_svc_decision_function(clf1)

​

​

探索模型

# 根据决策边界，对X中的样本进行分类，返回的结构为n_samples
clf.predict(x)

array([1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1,
       1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1,
       0, 1, 1, 0, 1, 0])

# 返回给定测试数据和标签的平均准确度
clf.score(x, y)

1.0

# 返回支持向量
clf.support_vectors_

array([[0.5323772 , 3.31338909],
       [2.11114739, 3.57660449],
       [2.06051753, 1.79059891]])

# 返回每个类中支持向量的个数
clf.n_support_

array([2, 1], dtype=int32)

推广到非线性情况

from sklearn.datasets import make_circles

x, y = make_circles(n_samples=300, factor=0.1, noise=0.1)
# x.shape(300, 2)
# y.shape(300,)

plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
plt.show()

​

​

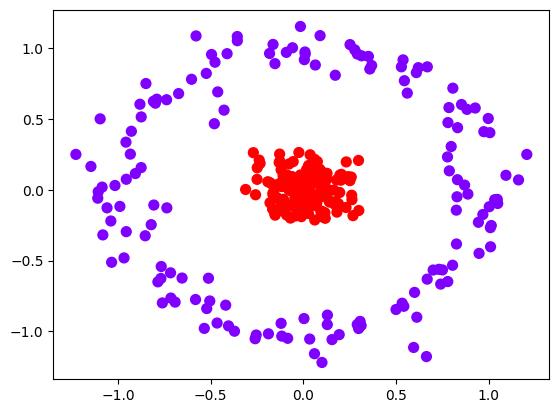
# 测试plot_svc_decision_function
clf = SVC(kernel="linear").fit(x, y)
plt.scatter(x[:, 0], x[:, 1], s=50, cmap="rainbow", c=y)
plot_svc_decision_function(clf)
clf.score(x, y)

0.6733333333333333

​

​

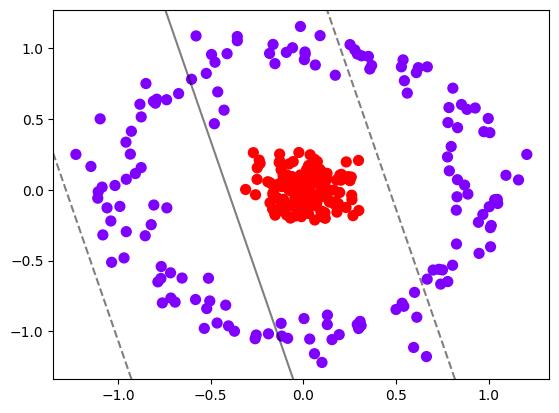
为非线性数据增加维度并绘制 3D 图像

r = np.exp(-(x**2).sum(1))  # r.shape(300,)
rlim = np.linspace(min(r), max(r), 100)

from mpl_toolkits import mplot3d


# 定义一个绘制三维图像的函数
# elev表示上下旋转的角度
# azim表示平行旋转的角度
def plot_3D(elev=30, azim=30, x=x, y=y):
    ax = plt.subplot(projection="3d")
    ax.scatter3D(x[:, 0], x[:, 1], r, c=y, s=50, cmap="rainbow")
    ax.view_init(elev=elev, azim=azim)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("r")
    plt.show()


plot_3D()

​

​

将上述过程放到 Jupyter Notebook 中运行

# 如果放到jupyter notebook中运行
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles

X, y = make_circles(100, factor=0.1, noise=0.1)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="rainbow")


def plot_svc_decision_function(model, ax=None):
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    Y, X = np.meshgrid(y, x)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
    ax.contour(
        X, Y, P, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"]
    )
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)


clf = SVC(kernel="linear").fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="rainbow")
plot_svc_decision_function(clf)
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r), max(r), 100)
from mpl_toolkits import mplot3d


def plot_3D(elev=30, azim=30, X=X, y=y):
    ax = plt.subplot(projection="3d")
    ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap="rainbow")
    ax.view_init(elev=elev, azim=azim)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("r")
    plt.show()


from ipywidgets import interact, fixed

interact(plot_3D, elev=[0, 30], azip=(-180, 180), X=fixed(X), y=fixed(y))
plt.show()

​

​

interactive(children=(Dropdown(description=\'elev\', index=1, options=(0, 30), value=30), IntSlider(value=30, de…

从线性 SVM 绘制 3D 决策边界

【中文标题】从线性 SVM 绘制 3D 决策边界

【英文标题】：Plotting 3D Decision Boundary From Linear SVM

【发布时间】：2016-07-13 22:35:11

【问题描述】：

我已经使用 sklearn.svm.svc() 拟合了 3 个特征数据集。我可以使用 matplotlib 和 Axes3D 绘制每个观察值的点。我想绘制决策边界以查看是否合适。我尝试调整 2D 示例来绘制决策边界，但无济于事。我知道 clf.coef_ 是一个垂直于决策边界的向量。我如何绘制它以查看它在哪里划分点？

【参考方案1】：

这是一个玩具数据集的示例。请注意，matplotlib 的 3D 绘图很时髦。有时，位于平面后面的点可能看起来好像在前面，因此您可能不得不摆弄旋转绘图以确定发生了什么。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.svm import SVC

rs = np.random.RandomState(1234)

# Generate some fake data.
n_samples = 200
# X is the input features by row.
X = np.zeros((200,3))
X[:n_samples/2] = rs.multivariate_normal( np.ones(3), np.eye(3), size=n_samples/2)
X[n_samples/2:] = rs.multivariate_normal(-np.ones(3), np.eye(3), size=n_samples/2)
# Y is the class labels for each row of X.
Y = np.zeros(n_samples); Y[n_samples/2:] = 1

# Fit the data with an svm
svc = SVC(kernel='linear')
svc.fit(X,Y)

# The equation of the separating plane is given by all x in R^3 such that:
# np.dot(svc.coef_[0], x) + b = 0. We should solve for the last coordinate
# to plot the plane in terms of x and y.

z = lambda x,y: (-svc.intercept_[0]-svc.coef_[0][0]*x-svc.coef_[0][1]*y) / svc.coef_[0][2]

tmp = np.linspace(-2,2,51)
x,y = np.meshgrid(tmp,tmp)

# Plot stuff.
fig = plt.figure()
ax  = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z(x,y))
ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob')
ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr')
plt.show()

输出：

编辑（上面评论中的关键数学线性代数语句）：

# The equation of the separating plane is given by all x in R^3 such that:
# np.dot(coefficients, x_vector) + intercept_value = 0. 
# We should solve for the last coordinate: x_vector[2] == z
# to plot the plane in terms of x and y.

【讨论】：

感谢您的出色回答和非常清晰的解释！我误会了拦截的意思！

非常感谢切斯特。只有一个小错误或错字：(-svc.intercept_[0]-svc.coef_[0][0]*x-svc.coef_[0][1] *y )/ svc.coef_[0][2]

对于 Python 3，所有索引除法都应使用“//”运算符进行编码，以使用隐式地板进行整数除法。

惊人的清晰答案。关于线性代数的评论没有写在其他任何地方。我在问题结束时将其隔离，并尝试使其更笼统。

【参考方案2】：

您无法将许多特征的决策面可视化。这是因为维度会太多，无法可视化 N 维表面。

但是，您可以使用 2 个特征并绘制漂亮的决策曲面，如下所示。

我在这里也写了一篇关于这个的文章： https://towardsdatascience.com/support-vector-machines-svm-clearly-explained-a-python-tutorial-for-classification-problems-29c539f3ad8?source=friends_link&sk=80f72ab272550d76a0cc3730d7c8af35

案例 1：2 个特征的 2D 图并使用 iris 数据集

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets

iris = datasets.load_iris()
X = iris.data[:, :2]  # we only take the first two features.
y = iris.target

def make_meshgrid(x, y, h=.02):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out

model = svm.SVC(kernel='linear')
clf = model.fit(X, y)

fig, ax = plt.subplots()
# title for the plots
title = ('Decision surface of linear SVC ')
# Set-up grid for plotting.
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)

plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_ylabel('y label here')
ax.set_xlabel('x label here')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
ax.legend()
plt.show()

案例 2：2 个特征的 3D 图并使用 iris 数据集

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from mpl_toolkits.mplot3d import Axes3D

iris = datasets.load_iris()
X = iris.data[:, :3]  # we only take the first three features.
Y = iris.target

#make it binary classification problem
X = X[np.logical_or(Y==0,Y==1)]
Y = Y[np.logical_or(Y==0,Y==1)]

model = svm.SVC(kernel='linear')
clf = model.fit(X, Y)

# The equation of the separating plane is given by all x so that np.dot(svc.coef_[0], x) + b = 0.
# Solve for w3 (z)
z = lambda x,y: (-clf.intercept_[0]-clf.coef_[0][0]*x -clf.coef_[0][1]*y) / clf.coef_[0][2]

tmp = np.linspace(-5,5,30)
x,y = np.meshgrid(tmp,tmp)

fig = plt.figure()
ax  = fig.add_subplot(111, projection='3d')
ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob')
ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr')
ax.plot_surface(x, y, z(x,y))
ax.view_init(30, 60)
plt.show()