MKL普通矩阵运算示例及函数封装
Posted GeoFXR
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MKL普通矩阵运算示例及函数封装相关的知识,希望对你有一定的参考价值。
本示例将介绍MKL中的矩阵乘法和求逆,使用MKL进行此类大型矩阵运算可大量节省计算时间和空间,但由于MKL中的原生API接口繁杂,因此将常用函数封装,便于后续使用,最后在实际例子中调用接口执行想要的矩阵运算。
1 MKL矩阵乘法案例
所用示例如下,矩阵A、B分别为
(1)matlab计算结果
作为标准答案,验证后续调用的正确性。
A=[1,-1,-3,0,0;
-2,5,0,0,0;
0,0,4,6,4;
-4,0,2,7,0;
0,8,0,0,-5;
1,0,0,0,0];
B=[1,-1,-3,0;
-2,5,0,0;
0,0,4,6;
-4,0,2,7;
0,8,0,0];
A*B
输出为:
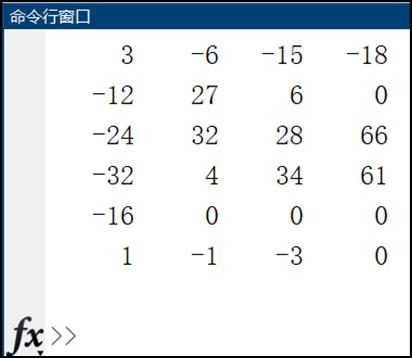
矩阵乘法接口
/*
输入:
MatrixA 矩阵A数据,类型为float型的二维数组
rowA 矩阵A的行数
colA 矩阵A的列数
MatrixB 矩阵B数据,类型为float型的二维数组
colC 矩阵C的列数
输出:
MatrixC 矩阵A*B数据,类型为float型的二维数组,为矩阵乘法计算结果
*/
bool MKL_MatrixMul(float **MatrixA, int rowA, int colA, float **MatrixB, int colC, float **MatrixC) ;
函数代码
函数将使用MKL库中的矩阵乘法接口cblas_?gemm实现,具体用法及参数详解见MKL库矩阵乘法(cblas_?gemm) - GeoFXR - 博客园 (cnblogs.com)
#include "MKL_Matrix_Methods.h"
//矩阵乘法
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC)
if (MatrixA == NULL)
return false;
if (MatrixB == NULL)
return false;
if (MatrixC == NULL)
return false;
int M = rowsA;
int N = colsA;
int K = colsC;
float *A = NULL;
float *B = NULL;
float *C = NULL;
int lda = N;
int ldb = K;
int ldc = K;
//由于mkl的矩阵乘法函数仅支持一维数组,需对输入进行转换
A = (float*)mkl_malloc(M*N * sizeof(float), 64);
B = (float*)mkl_malloc(N*K * sizeof(float), 64);
C = (float*)mkl_malloc(M*K * sizeof(float), 64);
if (A == NULL || B == NULL || C == NULL)
mkl_free(A);
mkl_free(B);
mkl_free(C);
return false;
//赋值
int i = 0;
int j = 0;
for (i = 0; i < M; i++)
memcpy(A + i * N, MatrixA[i], N * sizeof(float));
for (i = 0; i < N; i++)
memcpy(B + i * K, MatrixB[i], K * sizeof(float));
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A, lda, B, ldb,
0, C, ldc);
for (i = 0; i < M; i++)
memcpy(MatrixC[i], C + i * K, K * sizeof(float));
mkl_free(A);
mkl_free(B);
mkl_free(C);
return true;
main函数
#include "MKL_Matrix_Methods.h"
#include "alloc.h"
#define M 6
#define N 5
#define K 4
// 矩阵乘法
int main()
int rowsA = M, colsA = N;
int rowsB = N, colsB = K;
int rowsC = M, colsC = K;
float Atemp[M][N] =
1,-1,-3,0,0,
-2,5,0,0,0,
0,0,4,6,4,
-4,0,2,7,0,
0,8,0,0,-5,
1,0,0,0,0,
;
float Btemp[N][K] =
1,-1,-3,0,
-2,5,0,0,
0,0,4,6,
-4,0,2,7,
0,8,0,0
;
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
float **matrixB = alloc2float(colsB, rowsB);
memset(matrixB[0], 0, rowsB*colsB * sizeof(float));
memcpy(matrixB[0], Btemp, rowsB*colsB * sizeof(float));
float **matrixC = alloc2float(colsC, rowsC);
memset(matrixC[0], 0, rowsC*colsC * sizeof(float));
MKL_MatrixMul(matrixA, rowsA, colsA, matrixB, colsC, matrixC); //调用MKL矩阵乘法接口
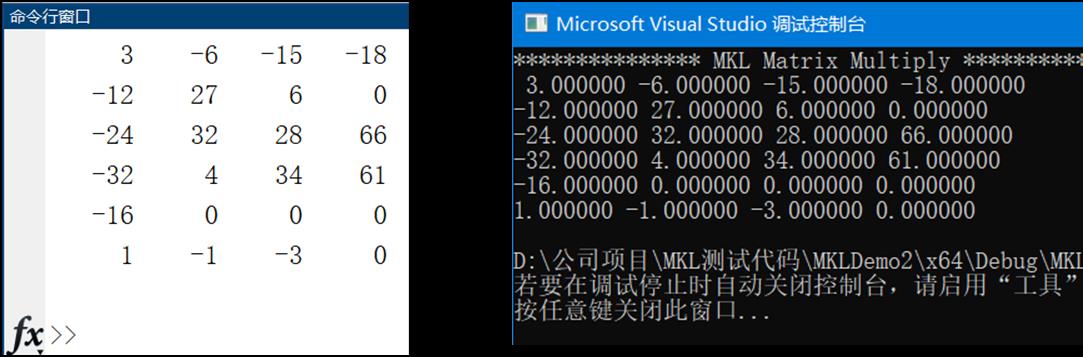
/* 输出结果 */
printf("*************** MKL Matrix Multiply ***************\\n ");
for (int i = 0; i < rowsC; i++)
for (int j = 0; j < colsC; j++)
printf("%f ", matrixC[i][j]);
printf("\\n");
free(matrixA);
free(matrixB);
free(matrixC);
2 MKL矩阵求逆案例
(1)matlab计算结果
作为标准答案,验证后续调用的正确性。
A = [1 2 4 0 0;
2 2 0 0 0;
4 0 3 0 0;
0 0 0 4 0;
0 0 0 0 5];
A_inv = inv(A)
输出为:
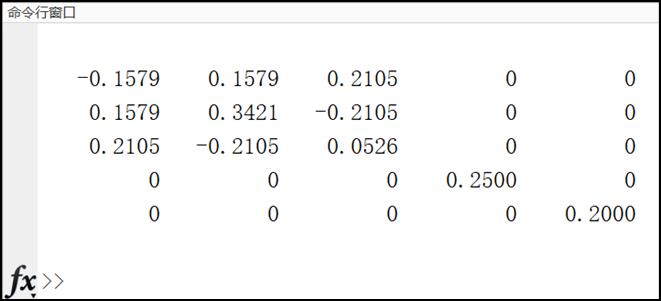
(2)MKL求逆
矩阵求逆接口
/*
函数功能:基于MKL库的矩阵求逆
输入:
Matrix 输入矩阵Matrix,n行n列
n 矩阵的行、列数
输出:
Matrix Matrix 的逆,n行n列
*/
bool MKL_MatrixInverse(float**Matrix, int n)
函数代码
使用MKL中的LAPACK库计算线性方程组\\(AX=B\\)的解,当\\(B\\)为单位阵时,\\(X\\)即为\\(A\\)的逆矩阵\\(A^-1\\)。函数使用的接口为LAPACKE_sgesv,具体参数详解见MKL库线性方程组求解(LAPACKE_?gesv) - GeoFXR - 博客园 (cnblogs.com)
bool MKL_MatrixInverse(float**Matrix, int n)
MKL_INT nrhs = n, lda = n, ldb = n;
// 创建置换矩阵,长度为n的数组
int *ipiv = (int*)mkl_malloc(n * sizeof(int), 64);
if (ipiv == NULL)
return false;
// 创建MKL矩阵
float *matA = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matA == NULL)
return false;
//将二维数组转换为一维MKL数组
for (int i = 0; i < n; i++)
memcpy(matA + i * n, Matrix[i], n * sizeof(float));
// 创建一个单位阵B
float *matEye = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matEye == NULL)
return false;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
matEye[i * n + j] = (i == j) ? 1.0 : 0.0;
// 调用求解AX=B函数
LAPACKE_sgesv(LAPACK_ROW_MAJOR, n, nrhs, matA, lda, ipiv, matEye, ldb);
// 将MKL矩阵转换回普通二维数组
for (int i = 0; i < n; i++)
memcpy(Matrix[i], matEye + i * n, n * sizeof(float));
// 释放内存
mkl_free(matA);
mkl_free(ipiv);
mkl_free(matEye);
return true;
main函数
#include "MKL_Matrix_Methods.h"
#include "alloc.h"
#define N 5
// 矩阵乘法
int main()
int rowsA = N, colsA = N;
float Atemp[N][N] =
1,2,4,0,0,
2,2,0,0,0,
4,0,3,0,0,
0,0,0,4,0,
0,0,0,0,5
;
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
//复制二维数组到二级指针
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
//求逆
MKL_MatrixInverse(matrixA, rowsA);
/* 输出结果 */
printf("*************** MKL Matrix Inverse ***************\\n ");
for (int i = 0; i < rowsA; i++)
for (int j = 0; j < colsA; j++)
printf("%f ", matrixA[j][i]);
printf("\\n");
free(matrixA);
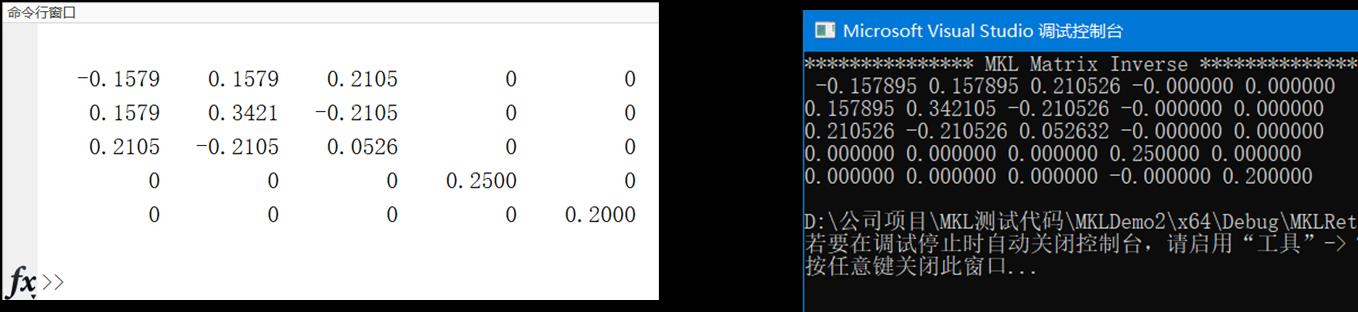
结果与matlab一致。
完整代码
Ⅰ MKL_Matrix_Methods.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include"mkl.h"
#include "mkl_types.h"
#include"mkl_lapacke.h"
bool MKL_MatrixMul(float **MatrixA, int rowA, int colA, float **MatrixB, int colC, float **MatrixC);
bool MKL_MatrixInverse(float**Matrix, int n);
Ⅱ MKL_Matrix_Methods.cpp
#include "MKL_Matrix_Methods.h"
//矩阵乘法
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC)
if (MatrixA == NULL)
return false;
if (MatrixB == NULL)
return false;
if (MatrixC == NULL)
return false;
int M = rowsA;
int N = colsA;
int K = colsC;
float *A = NULL;
float *B = NULL;
float *C = NULL;
int lda = N;
int ldb = K;
int ldc = K;
//由于mkl的矩阵乘法函数仅支持一维数组,需对输入进行转换
A = (float*)mkl_malloc(M*N * sizeof(float), 64);
B = (float*)mkl_malloc(N*K * sizeof(float), 64);
C = (float*)mkl_malloc(M*K * sizeof(float), 64);
if (A == NULL || B == NULL || C == NULL)
mkl_free(A);
mkl_free(B);
mkl_free(C);
return false;
//赋值
int i = 0;
int j = 0;
for (i = 0; i < M; i++)
memcpy(A + i * N, MatrixA[i], N * sizeof(float));
for (i = 0; i < N; i++)
memcpy(B + i * K, MatrixB[i], K * sizeof(float));
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A, lda, B, ldb,
0, C, ldc);
for (i = 0; i < M; i++)
memcpy(MatrixC[i], C + i * K, K * sizeof(float));
mkl_free(A);
mkl_free(B);
mkl_free(C);
return true;
//矩阵求逆
bool MKL_MatrixInverse(float**Matrix, int n)
MKL_INT nrhs = n, lda = n, ldb = n;
// 创建置换矩阵,长度为n的数组
int *ipiv = (int*)mkl_malloc(n * sizeof(int), 64);
if (ipiv == NULL)
return false;
// 创建MKL矩阵
float *matA = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matA == NULL)
return false;
//将二维数组转换为一维MKL数组
for (int i = 0; i < n; i++)
memcpy(matA + i * n, Matrix[i], n * sizeof(float));
// 创建一个单位阵B
float *matEye = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matEye == NULL)
return false;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
matEye[i * n + j] = (i == j) ? 1.0 : 0.0;
// 调用求解AX=B函数
LAPACKE_sgesv(LAPACK_ROW_MAJOR, n, nrhs, matA, lda, ipiv, matEye, ldb);
// 将MKL矩阵转换回普通二维数组
for (int i = 0; i < n; i++)
memcpy(Matrix[i], matEye + i * n, n * sizeof(float));
// 释放内存
mkl_free(matA);
mkl_free(ipiv);
mkl_free(matEye);
return true;
Ⅲ main.cpp
#include "MKL_Matrix_Methods.h"
#include "alloc.h"
#define M 6
#define N 5
#define K 4
void MKL_MatrixMul_Demo();
void MKL_MatrixInverse_Demo();
int main()
MKL_MatrixMul_Demo(); //矩阵乘法示例
MKL_MatrixInverse_Demo(); //矩阵求逆示例
//矩阵乘法
void MKL_MatrixMul_Demo()
int rowsA = M, colsA = N;
int rowsB = N, colsB = K;
int rowsC = M, colsC = K;
float Atemp[M][N] =
1,-1,-3,0,0,
-2,5,0,0,0,
0,0,4,6,4,
-4,0,2,7,0,
0,8,0,0,-5,
1,0,0,0,0,
;
float Btemp[N][K] =
1,-1,-3,0,
-2,5,0,0,
0,0,4,6,
-4,0,2,7,
0,8,0,0
;
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
float **matrixB = alloc2float(colsB, rowsB);
memset(matrixB[0], 0, rowsB*colsB * sizeof(float));
memcpy(matrixB[0], Btemp, rowsB*colsB * sizeof(float));
float **matrixC = alloc2float(colsC, rowsC);
memset(matrixC[0], 0, rowsC*colsC * sizeof(float));
MKL_MatrixMul(matrixA, rowsA, colsA, matrixB, colsC, matrixC); //调用MKL矩阵乘法接口
/* 输出结果 */
printf("*************** MKL Matrix Multiply ***************\\n ");
for (int i = 0; i < rowsC; i++)
for (int j = 0; j < colsC; j++)
printf("%f ", matrixC[i][j]);
printf("\\n");
free(matrixA);
free(matrixB);
free(matrixC);
// 矩阵求逆
void MKL_MatrixInverse_Demo()
int rowsA = N, colsA = N;
float Atemp[N][N] =
1,2,4,0,0,
2,2,0,0,0,
4,0,3,0,0,
0,0,0,4,0,
0,0,0,0,5
;
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
//复制二维数组到二级指针
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
//求逆
MKL_MatrixInverse(matrixA, rowsA);
/* 输出结果 */
printf("*************** MKL Matrix Inverse ***************\\n ");
for (int i = 0; i < rowsA; i++)
for (int j = 0; j < colsA; j++)
printf("%f ", matrixA[j][i]);
printf("\\n");
free(matrixA);
OpenCV中的MAT类矩阵的各种基本运算及示例代码(加减乘点乘点除乘方累加转置等)
OpenCV中的MAT类矩阵的各种基本运算及示例代码。
目录
- 01-两个矩阵相加、矩阵和标量相加
- 02-带权重(系数)的矩阵加法
- 03-两个矩阵的经典线性变换
- 04-两个矩阵相减、矩阵和标量相减
- 05- 求矩阵中每个元素的相反数
- 06-矩阵元素乘法(点乘)、矩阵与标量相乘
- 07-各种累积和
- 08-矩阵乘法
- 09-矩阵乘方
- 10-矩阵的元素除法(点除)【真除,既保留整数也保留小数】
- 11 -矩阵的元素除法(点除)取整
- 12-矩阵的元素除法(点除)取余
- 13-矩阵的转置
01-两个矩阵相加、矩阵和标量相加
可以使用函数add()实现两个矩阵相加,矩阵和标量相加。
详情见博文 https://blog.csdn.net/wenhao_ir/article/details/125246253
02-带权重(系数)的矩阵加法
可以用函数cv::addWeighted()实现带权重(系数)的矩阵加法,其官方文档介绍如下:

如果认真阅读了博文https://blog.csdn.net/wenhao_ir/article/details/125246253对函数add()的说明,应该很容易明白这个函数的使用,所以就就不做额外说明了,示例代码也不给了。
只是要注意下,它不能实现矩阵与标量的带权重(系数)的加法,并且两个相加的矩阵必须是相同尺寸和通道数的矩阵。当输出矩阵的数据类型为CV_32S时,不会对结果做saturate(饱和)操作,关于饱和操作,大家可参见博文 https://blog.csdn.net/wenhao_ir/article/details/125247806
03-两个矩阵的经典线性变换
可以用函数cv::scaleAdd()实现两个矩阵的经典线性变换,其官方文档介绍如下:

官方文档已经写得很清楚它的用法了,这里就先不上示例代码了,只要是要注意的三个矩阵的尺寸和数据类型都是一样的。
04-两个矩阵相减、矩阵和标量相减
可以用函数cv::subtract()实现两个矩阵相减、矩阵和标量相减,官方文档对其介绍如下:


从上面的文档介绍可以看出,其用法与cv::add()的用法一模一样,所以这里就不多介绍了,示例代码也暂时不给了。
05- 求矩阵中每个元素的相反数
OpenCV矩阵的元素数据类型有以下这些:
CV_8U、CV_8S、CV_16U、CV_16S、CV_32S、CV_32F、CV_64F
求相反数的话显然数据类型要为带符号的数据类型,上面的数据类型中有带符号的有:CV_8S、CV_16S、CV_32S、CV_32F、CV_64F。
可以用函数cv::subtract()的第四种形式实现求矩阵中每个元素的相反数,其第四种形式如下:

也可以直接用减号实现,当直接用减号时,实际上也是将操作符“-”重载为了函数cv::subtract()实现的。
示例代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1(2, 3, CV_8SC1, cv::Scalar(98));
cout << "A1中的数据为:\\n" << A1 << endl << endl;
//第一种方法实现求矩阵每个元素的相反数
cv::Mat B1 = -A1;
cout << "B1中的数据为:\\n" << B1 << endl << endl;
//第二种方法实现求矩阵中每个元素的相反数
cv::Mat C1;
cv::subtract(0,A1,C1);
cout << "C1中的数据为:\\n" << C1 << endl << endl;
return(0);
运行结果如下:

06-矩阵元素乘法(点乘)、矩阵与标量相乘
可以用函数cv::multiply()和函数cv::Mat::mul()实现矩阵元素乘法(点乘)、矩阵与标量相乘。
官方文档对其介绍如下:

上面的文档对函数cv::multiply()的介绍是比较清楚了,补充说明几点:
①其两个输入矩阵要求是相同的尺寸和相同的通道数,注意数据类型可以不一样,当数据类型不一样时,还是像函数add()那样,由参数dtype来指定输出矩阵的类型。
②如何使用这个函数实现矩阵与标量相乘?很简单,按照下面这个公式:
dst
(
I
)
=
saturate
(
scale
⋅
src1
(
I
)
⋅
src2
(
I
)
)
\\textttdst (I)= \\textttsaturate ( \\textttscale \\cdot \\textttsrc1 (I) \\cdot \\textttsrc2 (I))
dst(I)=saturate(scale⋅src1(I)⋅src2(I))
我们只需要把其中一个矩阵设为全1的矩阵就行了嘛。
③函数mul()是函数multiply()的友好变体,下面这句代码:
cv::multiply(A1, B1, C1, scale1);
等效于:
cv::Mat C1 = A1.mul(2 * B1);
07-各种累积和
07-1-矩阵和的累加
可以用函数cv::accumulate()实现矩阵各元素和的累加,其官方文档介绍下:

示例代码暂时不给,要特别注意的是数据类型应该为浮点型。
07-1-对矩阵的点乘结果进行累加
可以利用函数cv::accumulateProduct()实现对矩阵各元素点乘的结果进行累加,函数cv::accumulateProduct()的官方文档如下:

同样要注意数据类型为浮点型,示例代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1 = (cv::Mat_<float>(2, 3) << 1, 2, 3, 4, 5, 6);
cout << "A1中的数据为:\\n" << A1 << endl << endl;
cv::Mat B1 = (cv::Mat_<float>(2, 3) << 2, 3, 4, 5, 6, 7);
cout << "B1中的数据为:\\n" << B1 << endl << endl;
cv::Mat C1 = (cv::Mat_<float>(2, 3) << 3, 4, 5, 6, 7, 8);
cout << "没做累加前C1中的数据为:\\n" << C1 << endl << endl;
cv::accumulateProduct(A1, B1, C1);
cout << "做了累加后C1中的数据为:\\n" << C1 << endl << endl;
return(0);
运行结果如下:

07-3 按alpha比例累加(带权重的累加)
可以用函数cv::accumulateWeighted()实现矩阵元素按alpha比例累加(带权重的累加),其官方文档如下:

示例代码就不暂时不给了,同样要注意数据类型需要为浮点型。
还有上面文档中的running average我觉得可以翻译为滑动平均。
07-4 矩阵各元素平方值的累加
可以用函数accumulateSquare()实现各元素平方值的累加,其官方文档如下:

示例代码就不暂时不给了,同样要注意数据类型需要为浮点型。
08-矩阵乘法
可以用运算符“*”实现矩阵乘法,示例代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1 = (cv::Mat_<float>(2, 3) << 1, 2, 3, 4, 5, 6);
cout << "A1中的数据为:\\n" << A1 << endl << endl;
cv::Mat B1 = (cv::Mat_<float>(3, 2) << 2, 3, 4, 5, 6, 7);
cout << "B1中的数据为:\\n" << B1 << endl << endl;
cv::Mat C1 = A1*B1;
cout << "C1中的数据为:\\n" << C1 << endl << endl;
return(0);
注意:类型必须为浮点型,即可以为“CV_32F或CV_64F”,而且似乎只支持一通道或两通道,三通道似乎不支持,因为我把上面的float改为uchar,那么报错如下:

运行结果如下:

我们手工验证下第一个结果:
12+24+3*6=2+8+18=28
可见的确做的是矩阵标准乘法。
09-矩阵乘方
想实现以矩阵A中的元素为底数,以矩阵B中元素为指数,但是目前没有找到相关函数。等以后找到了再写到这里吧…
10-矩阵的元素除法(点除)【真除,既保留整数也保留小数】
可以用函数cv::divide()和函数cv::mul()实现矩阵的元素除法(点除),其官方文档如下:

它的用法与函数cv::multiply()基本一样,所以它需要注意的地方请参见对函数cv::multiply()的介绍。
示例代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1 = (cv::Mat_<float>(2, 3) << 1, 2, 3, 4, 5, 6);
cout << "A1中的数据为:\\n" << A1 << endl << endl;
cv::Mat B1 = (cv::Mat_<float>(2, 3) << 2, 3, 4, 5, 6, 7);
cout << "B1中的数据为:\\n" << B1 << endl << endl;
cv::Mat C1;
double scale = 2;
cv::divide(B1, A1, C1, scale);
cout << "C1中的数据为:\\n" << C1 << endl << endl;
cv::Mat C2 = B1.mul(scale / A1);
cout << "C2中的数据为:\\n" << C1 << endl << endl;
return(0);
运行结果如下:

从以上运行结果可以看出:
代码:
cv::divide(B1, A1, C1, scale);
等效于代码:
cv::Mat C2 = B1.mul(scale / A1);
我们把数据类型换为uchar,再看下结果,代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1 = (cv::Mat_<uchar>(2, 3) << 1, 2, 3, 4, 5, 6);
cout << "A1中的数据为:\\n" << A1 << endl << endl;
cv::Mat B1 = (cv::Mat_<uchar>(2, 3) << 2, 3, 4, 5, 6, 7);
cout << "B1中的数据为:\\n" << B1 << endl << endl;
cv::Mat C1;
double scale = 2;
cv::divide(B1, A1, C1, scale);
cout << "C1中的数据为:\\n" << C1 << endl << endl;
cv::Mat C2 = B1.mul(scale / A1);
cout << "C2中的数据为:\\n" << C1 << endl << endl;
return(0);

对比浮点型的结果:

发现做得是五舍六入~
11 -矩阵的元素除法(点除)取整
这个目前博主没有发现相关函数,不过可以先做元素真除,然后用下面三个函数实现
向上取整函数cvCeil()
向下取整函数cvFloor()
四舍五入函数cvRound()
12-矩阵的元素除法(点除)取余
这个目前博主没有发现相关函数,想了下似乎只能每个元素与每个元素单独作系统库运算“%”。
13-矩阵的转置
可以用函数cv::transform()实现矩阵的转置。
官方文档如下:

示例代码如下:
//OpenCV版本:3.0.0
//VS版本:2013
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
int main()
cv::Mat A1 = (cv::Mat_<uchar>(2, 3) << 1, 2, 3, 4, 5, 6);
cout << "A1中的数据为:\\n" << A1 << endl << endl;
cv::Mat B1;
cv::transpose(A1, B1);
cout << "B1中的数据为:\\n" << B1 << endl << endl;
return(0);
运行结果如下:

延伸阅读:
Python的Numpy库中各种矩阵基本运算的示例代码(加、减、乘、点乘、点除、乘方、转置等)
归纳总结MATLAB中与矩阵运算有关的算术运算符(加、减、乘、除、点乘、点除、乘方、转置等)
以上是关于MKL普通矩阵运算示例及函数封装的主要内容,如果未能解决你的问题,请参考以下文章