MATLAB中函数taylor(f)的作用

Posted 2023-04-23

在MATLAB中，taylor()是对符号表达式（函数）进行泰勒级数展开的命令。现在介绍taylor对3个常见函数做泰勒级数展开。
一·符号运算
1、符号运算基本语法
数值运算必须先对变量赋值再运算，然后才能参与运算。符号运算无须事先的运算对象可以使没有赋值的符号变量，可以获得任意精度的解。
①符号表达式可以代表数字、函数、算子、变量的matlab字符串。
②建立单个符号量：符号量名 = sym(‘符号表达式’)。
syms 符号表达式1 符号表达式2 符号表达式3 表达式4；
2、符号矩阵
符号矩阵也是一种符号表达式，所以前面介绍符号表达式运算也可以在矩阵意义下进行，但应该注意这些函数作用于符号矩阵时，是分别用于矩阵的每个元素。比如A =sym(‘[a,3*b;3*a,c]’);由于符号矩阵是一个矩阵，所以它可以进行矩阵相关运算(diag，tril，det等函数)。
numeric(A)：将符号矩阵转化为数值矩阵。
tranpose(A):返回A的装置矩阵
determ(A):返回矩阵的行列式值
3、符号表达式的4则运算
对符号表达式或或符号矩阵A进行因式分解：factor(A);
对符号表达式或符号矩阵A进行展开：expand(A)
对符号表达式或符号矩阵A进行合并同类项：collect(A)
应用函数规则对A进行简化：simplify(A)
对函数进行综合简化：simple(A)
对函数f关于x求n阶导数：diff(f,x,n)
求积分最常用函数：int(f,r,x0,x1) 其中f为积分表达，r为积分变量，
x0和x1为积分上下限。没有上下限则求得的是不定积分。
subs(f,x,x的实际值)给表达式中的x赋实际值并计算。
二、复数运算
1、基本运算操作
复数表达式构造利用i，j直接写，也可以额利用符号函数来构造。也可以写成极坐标的形式。
polar(theta,rho)画出极坐标图，其中theta为极坐标极角，rho为极坐标失径。
real(A)求复数A的实部 conj(A) 求A的共轭
imag(A) 求复数A的虚部 abs(A)求A的模
angle(A) 求A的相角
[r,p,k]= residue([an-1,…,a0],[bn-1,…,b0]);求解有理分式的留数。其中r为留数，p对应的各奇点。
2、泰勒展开和Fourier变换
taylor(f):返回函数f的五次多项式近似，函数f的自变量有函数findsym决定。
taylor(f,n)：返回n-1次幂多项式，函数f自变量由findsym决定。
taylor(f,a):返回a点附近的五次幂多项式近似。
taylor(f,x):返回指定变量x的五次幂多项式近似。
fourier(f):返回以默认变量x为数量符号f的Fourier变换，其中变换后函数默认以w为自变量。
fourier(f,v):以v替代w为变换后的函数自变量。
fourier(f,u,v):以v替代w，以u提到x
ifourier也是类似的。
拉普拉斯变换用法：laplace 和ilaplace都是类似的。
Z变换用法：ztrans和iztrans也是类似的。
三、matlab的绘图
1、plot(x1,y1,option1,x2,y2,option2);画二维曲线
2、plot3(x1,y1,z1,option1,x2,y2,z2,option2);画三维 曲线
3、mesh(X,Y,Z,C)；画三维网格曲面X,Y,Z为矩阵
4、surf(X,Y,Z,C);画三维阴影曲面，X,Y,Z为矩阵
5、[X,Y]=meshgird(x,y)；将矩阵X的每一行都为向量x
6、view(beta,theta),选择三维图角度，其中beta为方位角，theta为视角。
7、hist(Y,X)以X为统计范围统计，绘制出Y分布直方图
8、rose(thera，x)以向量x为统计范围，在极坐标下统计thera的直方图分布。
9、bar(data,’mode’)用来画柱状图，mode默认是‘grouped’模式，这时bar函数把数组data每一行看作一组，画在一个水平坐标位置。若指定为‘stacked’则把每一组数据叠加起来绘图。barh水平放置的柱状图。三维柱状图bar3() bar3h()也是类似。
10、面积图 area()函数用于绘制面积图，和累叠模式柱状图类似，面积图也是把每一组数据点累叠绘制。不过它把每一个数据集合的相邻点用线条连起来，并且把每一个数据集合所在区域用不同颜色填充。
11、pie()绘制二维饼图。pie3()绘制三维饼图。
12、火柴干图：把每个数据点用一个垂直于横轴的火柴棒表示，stem(),stem3()。
13、绘制阶梯图stairs()。
14、等高线图：用于显示多元函数的函数值变化趋势，contour()来绘制等高线，clabel()标注等高线函数值，contourf绘制颜色填充模式。
15、axis[xmin xmax ymin ymax]：分别限定x轴和y轴的范围
axis equal：横纵坐标单位长度相同
axis square:图框呈方形
axis off:清除坐标刻度
semilogx:x轴为对数坐标
semilogy:y轴为对数坐标
loglog:全对数坐标
text(x,y,’标识文本’)在指定坐标标识对应的数据点
gtext(‘标识文本’)绘图后用鼠标来标识对应的位置
title(”)图形标题，xlabel(”)标识x轴，ylabel(”)表示y轴
legend(‘图例一’，图例二’)给曲线添加图例
grid on 给当前坐标加上珊格线
grid off 从当前坐标中删去珊格线
hold on 保持图像，便于绘制多条曲线
hold off 取消保持
四、matlab函数及调用
1、匿名函数:匿名函数可以接受多个输入和输出参数，适用于命令行操作。fhandle = @(arglist) expression
2、私有函数：具有访问限制性访问权限的函数，他们对应的M文件保存在名为private的文件夹下，但它只能被private文件下M文件调用。
3、输入输出参数目录：**nargin：输入参数数目，nargout：输出参数数目。
4、可变输入参数：**varargin:可变输入参数。varargout可变输出参数。
5、全局变量：用global来声明和调用
6、函数句柄：函数句柄提供了一种间接调用函数的方法，创建函数句柄需要用到@，匿名函数其实也是一种句柄，而对M文件的各种函数都可以创建函数句柄，从而可以通过函数句柄对这些函数实现间接调用。fhandle =@function_filename;
feval(fhandle,parameters);调用函数句柄
五、matlab调试方法和编程技巧
1·去掉分号输出中间结果。
2·设置断点逐步调试，观测变量值的变化。
3、Code Analyzer:可以分析M文件的性能和错误。
4、Profiler:MATLAB提供的一个功能强大的代码分析工具，一般来说，应该尽量避免不必要的变量输出、循环赋值前预定义数组尺寸，多采用向量化的，matlab函数，少采用数组，提高matlab的性能。
5、一个程序的执行速度取决于它所调用的子程序个数以及所采用的算法 ，通常希望程序越少越好，算法效率越高越好。可以使用嵌套计算减小乘法次数。tic初始化时钟开始计时，toc时钟停止，获得执行时间。
6、matlab要尽量避免使用循环，为了得到最快的运行速度，在for循环运行之前,应该预先分配数组。矩阵运算优先考虑内联函数。
7、程序应该具有一定容错能力，当用户输入错误时，应该使用error()函数来提示出国原因。 参考技术A taylor(f)幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。

定位问题基于matlab chan算法fang算法taylor算法求解目标定位问题含Matlab源码 2135期

一、chan+taylor算法移动基站无源定位简介

1 引言
随着无人机的普及，低空空域的安全问题受到人们的极大关注．针对该问题，本研究对“非合作型”无人机采用一种基于时差法的无源定位算法对其进行实时定位．基于时差法的无源定位方法是根据求解无人机信号到达主站和各辅站的距离差，并联合各基站坐标所构成的双曲线方程组来实现．该方法定位精度高，且不对外发射信号，可在机场等区域安全使用．

目前，Chan算法和Taylor算法是2种经典的时差定位算法．其中，Chan算法在时差值精确的情况下，可以实现较高精度的定位，但如果时差值精度不够，其定位精度会大幅降低．Taylor算法则是在已有的定位坐标基础上，进行迭代递归，使定位出的坐标接近于目标的真实坐标．虽然Taylor算法定位精度较高，但需要提供初始估计坐标，否则就无法实现准确定位．基于2种算法的特点，本研究提出Chan-Taylor联合算法，其思路是，将Chan算法解算出的目标坐标作为初始估计坐标值赋给Taylor算法进行迭代运算，即使获取的时差值存在一定误差，使初始估计坐标的精度不高，但可以通过迭代来提高定位坐标的精度．通过算法对比和仿真分析表明，Chan-Taylor联合算法较Chan算法具有更高的定位精度和稳定性，较Taylor算法更具有实用性．

2 算法描述
2.1 Chan算法
基于Chan算法的无源定位是通过求解目标源信号到达辅站与主站之间的时差并联立各基站坐标所得的双曲线方程组来实现的．该算法是一种非迭代算法，不需要初始值，在时差精确、视距传输的情况下，其定位效果良好，但在工程上，很难获得满足要求的时差初值．因此，Chan算法可作为其他算法的前置条件．

本研究以4站三维定位系统为例建立3组方程，该方程组为超定方程组．通常情况下，由于该方程组导出的矩阵不存在逆矩阵，方程组无法正常求解．所以，本研究利用伪逆法联合最小二乘法对方程组进行解算，即Chan算法．4站定位系统的定位原理如图1所示．

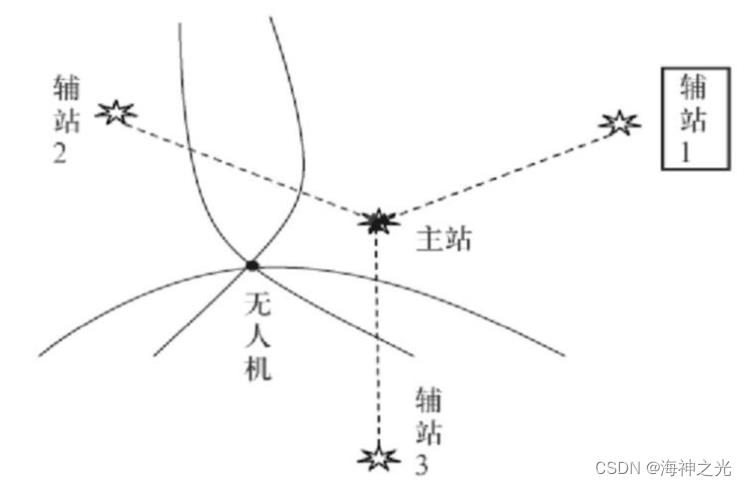
图1 4站定位系统示意图
图1中，主站坐标联立3个辅站坐标，通过分别计算出的时差可构建3条双曲线，其交点就是无人机的位置．

假设无人机位置为P=[px,py,pz]，各基站坐标为Pi=[pix,piy,piz],i∈[0,3]，则无人机到基站i的距离ri2可表示为，

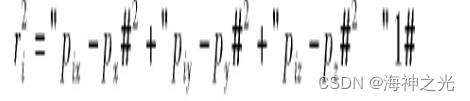
本研究若不特别指明，均默认i∈[1,3]．对式(1)整理可得，

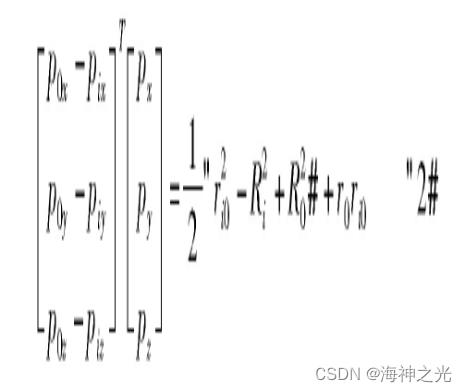
式中，Ri表示基站i到坐标原点的距离;R0为主站到坐标原点的距离;ri0为无人机到辅站与主站间的距离差．

4站三维定位系统存在一个由3组式(2)的关系式结合而成的方程组，如式(3)所示．当A≠0时，线性方程组(3)有解．

式中，A是方程组的系数矩阵，b是方程组的输出向量．

利用伪逆法可求得无人机坐标为，

2.2 Chan-Taylor联合算法
因为Chan算法是非递归算法，对时差精度要求高，因此，本研究对该算法的定位结果进行二次处理．Taylor算法是利用局部最小二乘解进行迭代[5]的递归算法，其定位精度高，但需要初始估计坐标，否则无法进行定位．

基于低空无人机时差定位的实际需求，本研究结合Chan算法和Taylor算法提出了一种改进的算法，即Chan-Taylor联合算法．Chan-Taylor联合算法是将Chan算法的解算结果作为初始估计坐标送入Taylor算法，以达到对无人机坐标进行误差计算和定位修正的作用．算法在迭代时，将误差与设定的阈值进行比较，若误差值大于阈值，则继续迭代;若误差值小于设定阈值，则终止迭代并输出结果．

2.3 Chan-Taylor联合算法流程及计算原理
Chan-Taylor联合算法流程如图2所示，具体为:首先，算法获得无人机信号到主站与各辅站之间的时差;然后，将时差用于Chan算法部分进行初始估计坐标值的计算，并利用该坐标值在Taylor算法部分做误差向量的计算，用以定位修正;同时，对误差进行阈值比较．如不满足条件，则继续迭代，如满足条件，则结束迭代，并输出最终结果．

图2 Chan-Taylor算法流程

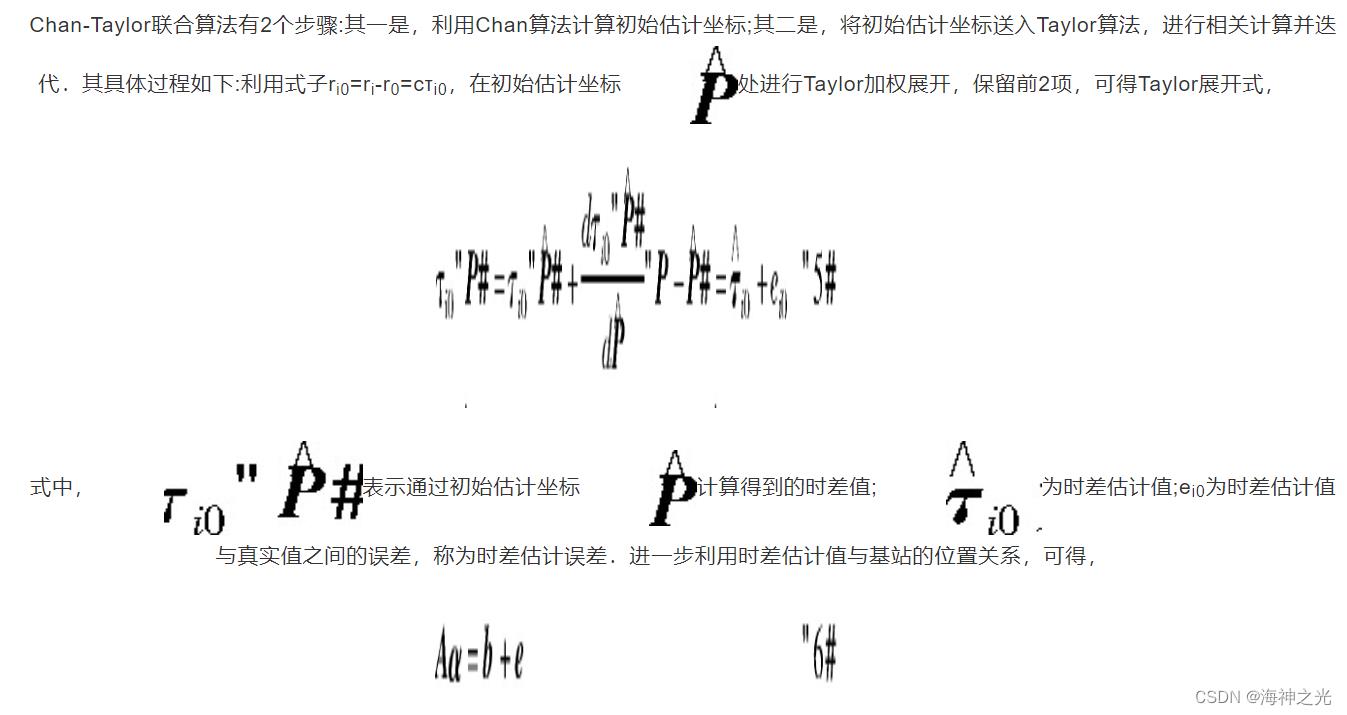
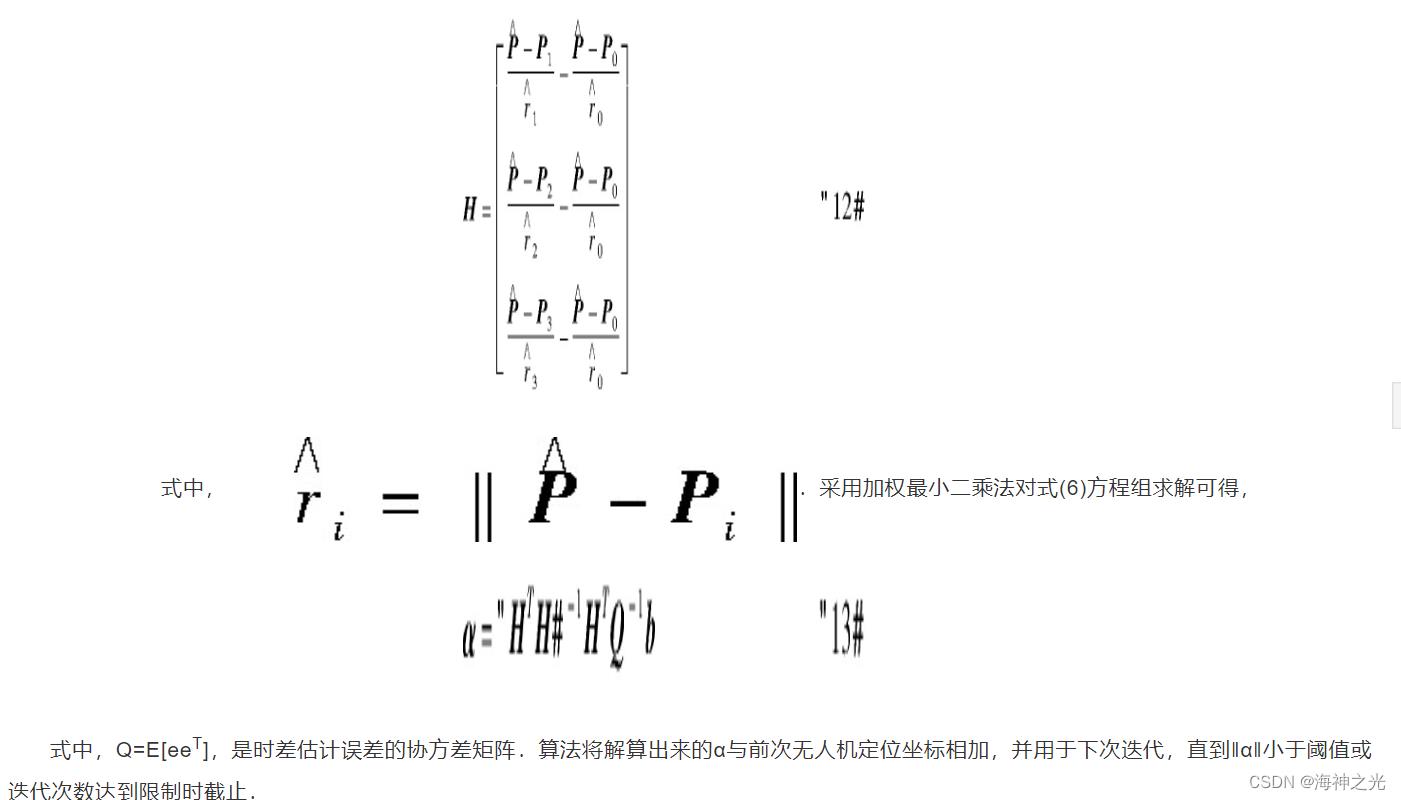
式中，α为目标差值向量，b为时差的差值向量，e为时差估计误差向量，H为时差估计的梯度矩阵．它们可分别表示为，

由式ri0=ri-r0=cτi0与站址坐标，可得，

将式(10)与式(11)联立，化简可得，

二、部分源代码

clear;clc;
C = 300000000; % 光速(米每秒)
R = [1000 2000 3000 4000 5000]; % 小区半径（米）
sgma =30;
Rn =1; %(km)
x_delta = 0;
y_delta = 0;
e = 0;
% 随机产生MS的位置（x，y）
u = rand(1);
y = (R/2)(1-sqrt(u))
v = (sqrt(3)((R/2)-y))rand(1);
x = sqrt(3)y + v
num = 5;
PPP=1000;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Chan定位算法
for i = 1:num
% 蜂窝系统各基站坐标
X1 = 0;
Y1 = 0;
X2 = R(i)(1+sqrt(3)/2);
Y2 = 0;
X3 = R(i)(sqrt(3)/2);
Y3 = R(i)(-3/2);
X4 = R(i)(-sqrt(3)/2);
Y4 = R(i)(-3/2);
X5 = R(i)(-1-(sqrt(3)/2));
Y5 = 0;
X6 = R(i)(-sqrt(3)/2);
Y6 = R(i)(3/2);
X7 = R(i)(sqrt(3)/2);
Y7 = R(i)(3/2);
% 计算MS到各基站的距离
R1 = distance(X1,Y1,x(i),y(i));
R2 = distance(X2,Y2,x(i),y(i));
R3 = distance(X3,Y3,x(i),y(i));
R4 = distance(X4,Y4,x(i),y(i));
R5 = distance(X5,Y5,x(i),y(i));
R6 = distance(X6,Y6,x(i),y(i));
R7 = distance(X7,Y7,x(i),y(i));

% KM = XM^2 + YM^2
K1 = Ka(X1,Y1);
K2 = Ka(X2,Y2);
K3 = Ka(X3,Y3);
K4 = Ka(X4,Y4);
K5 = Ka(X5,Y5);
K6 = Ka(X6,Y6);
K7 = Ka(X7,Y7);
% XM_1 = XM - X1；YM_1 = YM - X1
X2_1 = Xab(X2,X1);
Y2_1 = Xab(Y2,Y1);
X3_1 = Xab(X3,X1);
Y3_1 = Xab(Y3,Y1);
X4_1 = Xab(X4,X1);
Y4_1 = Xab(Y4,Y1);
X5_1 = Xab(X5,X1);
Y5_1 = Xab(Y5,Y1);
X6_1 = Xab(X6,X1);
Y6_1 = Xab(Y6,Y1);
X7_1 = Xab(X7,X1);
Y7_1 = Xab(Y7,Y1);
t_sgma=10^(-7);
% 各TDOA测量值的方差
D_med1= 1.82*(0.410^{(-6)*(R1/1000)}0.5)^2;
D_med2= 1.82(0.410^{(-6)*(R2/1000)}0.5)^2;
D_med3= 1.82(0.410^{(-6)*(R3/1000)}0.5)^2;
D_med4= 1.82(0.410^{(-6)*(R4/1000)}0.5)^2;
D_med5= 1.82(0.410^{(-6)*(R5/1000)}0.5)^2;
D_med6= 1.82(0.410^{(-6)*(R6/1000)}0.5)^2;
D_med7= 1.82(0.410^{(-6)*(R7/1000)}0.5)^2;
T2_1_fangcha = D_med2+D_med1+2t_sgma^2;
T3_1_fangcha = D_med3+D_med1+2t_sgma^2;
T4_1_fangcha = D_med4+D_med1+2t_sgma^2;
T5_1_fangcha = D_med5+D_med1+2t_sgma^2;
T6_1_fangcha = D_med6+D_med1+2t_sgma^2;
T7_1_fangcha = D_med7+D_med1+2*t_sgma^2;

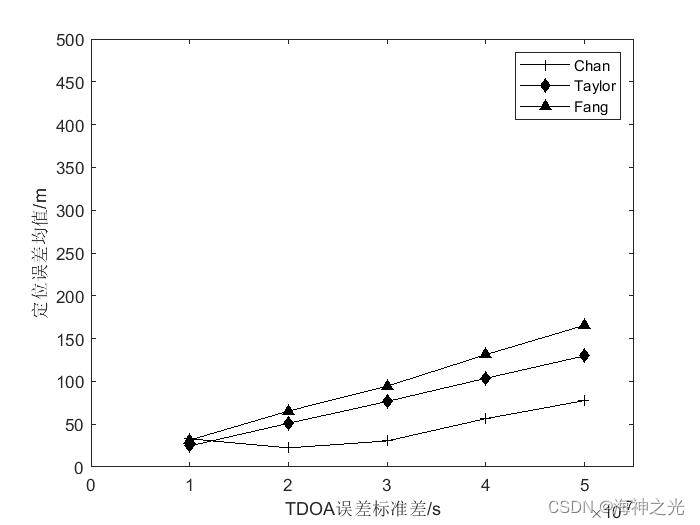
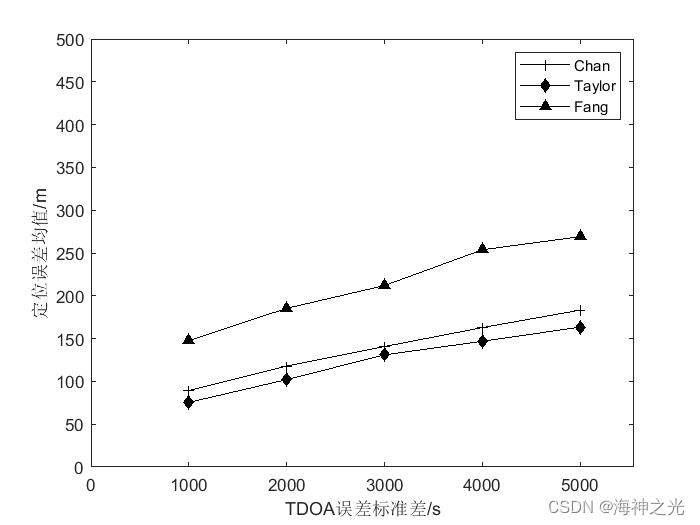
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 罗正华,雷林,周方均,李霞.基于Chan-Taylor联合算法的低空无人机时差定位研究[J].成都大学学报(自然科学版). 2019,38(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除