python实现图广度优先遍历深度优先遍历

Posted 2020-11-13 农夫三拳有點疼

一、广度优先遍历-BFS

　　顾名思义，BFS总是先访问完同一层的结点，然后才继续访问下一层结点，它最有用的性质是可以遍历一次就生成中心结点到所遍历结点的最短路径，这一点在求无权图的最短路径时非常有用。广度优先遍历的核心思想非常简单，用python实现起来也就十来行代码。下面就是超精简的实现，用来理解核心思想足够了：

 1 import queue
 2  
 3 def bfs(adj, start):
 4     visited = set()
 5     q = queue.Queue()
 6     q.put(start) #把起始点放入队列
 7     while not q.empty():
 8         u = q.get()
 9         print(u)
10         for v in adj.get(u, []):
11             if v not in visited:
12                 visited.add(v)
13                 q.put(v)
14  
15  
16 graph = {1: [4, 2], 2: [3, 4], 3: [4], 4: [5]}
17 bfs(graph, 1)

　　上面的代码：

1. 创建一个队列，遍历的起始点放入队列

2. 从队列中取出一个元素，打印它，并将其未访问过的子结点放到队列中

3. 重复2，直至队列空

　　时间复杂度：基本与图的规模成线性关系了，比起图的其它算法动不动就O(n^2)的复杂度它算是相当良心了

　　空间复杂度：我们看到程序中使用了一个队列，这个队列会在保存一层的结点，当图规模很大时占用内存还是相当可观的了，所以一般会加上一些条件，比如遍历到第N层就停止

 

关于图的理解的一个技巧
　　上面提到，BFS遍历会由近及远，同一层会先遍历完。这里随便提一个关于图的展示问题，或者说当你拿到一个图，当你要对它进行分析时，这个图在你的脑海里会一个什么形态呢？比较一下下面两种形态，你觉得哪一种更加清晰

 

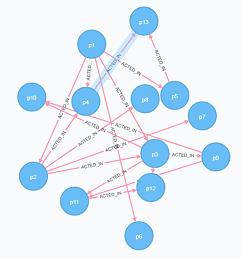
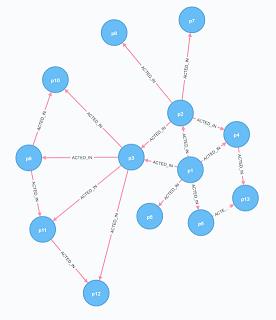
　　其实你仔细看，上下两张图其实数据是一样的，只是布局不一样罢了，上面的图使用了一种无规律凌乱的布局，而下面假设出了一个中心点，将与它直接相连的结点放在第一层上，与它距离为2的结点放在第二层了，这样会有什么好处呢？好处就是这样布局后边只会在相邻层或者同一层间的结点间相连，这样就不会出现很长或者交叉的边了，整个图会感觉有序得多，在思考图的一些性质的时候也会清晰得多。

　　回过头来，这种布局不说是BFS形成的吗。

二、深度优先遍历-DFS

　　深度优先遍历算法DFS通俗的说就是“顺着起点往下走，直到无路可走就退回去找下一条路径，直到走完所有的结点”。这里的“往下走”主是优先遍历结点的子结点。BFS与DFS都可以完成图的遍历。DFS常用到爬虫中，下面是最精简的代码：

 1 def dfs(adj, start):
 2     visited = set()
 3     stack = [[start, 0]]
 4     while stack:
 5         (v, next_child_idx) = stack[-1]
 6         if (v not in adj) or (next_child_idx >= len(adj[v])):
 7             stack.pop()
 8             continue
 9         next_child = adj[v][next_child_idx]
10         stack[-1][1] += 1
11         if next_child in visited:
12             continue
13         print(next_child)
14         visited.add(next_child)
15         stack.append([next_child, 0])
16  
17  
18 graph = {1: [4, 2], 2: [3, 4], 3: [4], 4: [5]}
19 dfs(graph, 1)　

　　上面的代码是dfs的非递归实现，其实递归的代码更简单，但是我觉得使用了函数的递归调用隐含了对栈的使用但是却没有明确出来，这样不太利于对dfs核心思想的理解，所以这里反而选择了更复杂的非递归实现。

　　整个程序借助了一个栈，由于python没有直接的实现栈，这里使用了list来模拟，入栈就是向列表中append一个元素，出栈就是取列表最后一个元素然后pop将最后一个元素删除。　

　　下面来分析实现过程，还是按之前的那句话“顺着起点往下走，直到无路可走就退回去找下一条路径，直到走完所有的结点”，整个程序都蕴含在这句话中：

　　首次是“顺着起点往下走”中的起点当然就是函数传进来的参数start，第三行中我们把起点放到了栈中，此时栈就是初始状态，其中就只有一个元素即起点。那么栈中元素表示的语义是：下一次将访问的结点，没错就这么简单，那么为什么我们一个结点和一个索引来表示呢？理由是这样的，由于我们使用邻接表来表示图，那么要表示一个结点表可以用<这个结点的父结点、这个结是父结点的第几个子结点>来决定，至于为什么要这么表示，就还是前面说的：由这们这里使用的图的存储方式-邻接表决定了，因为这样我们取第N个兄弟结点要容易了。因为邻接表中用list来表示一个结点的所有子结点，我们就用一个整数的索引值来保存下次要访问的子结点的list的下标，当这个下标超过子结点list的长度时意味着访问完所有子结点。 

　　接着，“往下走”，看这句：next_child = adj[v][next_child_idx]就是我们在这个while循环中每次访问的都是一个子结点，访问完当前结点后stack.append([next_child, 0])将这个结点放到栈中，意思是下次就访问这个结点的子结点，这样就每次都是往下了。　　

　　“直到无路可走”，在程序中的体现就是 if (v not in adj) or (next_child_idx >= len(adj[v])):，栈顶元素表示即将要访问的结点的父结点及其是父结点的第N个子结点（有点绕），这里的意思是如果这个父结点都没有子结点了或者是我们想要访问第N个子结点但是父结点并没有这么多子结点，表示已经访问完了一个父结点的所有子结点了。

　　接着“就退回去找下一条路径”中的“退回去”，怎么退回去，很简单将栈顶元素弹出，新的栈顶元素就是它的父结点，那么就是退回去了，“去找下一条路径”就是弹出栈顶后下一次while中会沿着父结点继续探索，也就是去找下一条路径了。

　　最后“直到走完所有的结点“当然就是栈为空了，栈为空表示已经回退到起点，即所有结点已经访问完了，整个算法结束。