暗的连锁 题解

Posted 2023-04-22 XiaoQuQu

题目描述

Dark 是一个无向图，图中有 \\(n\\) 个结点和两类边，一类边被称为主要边，而另一类被称为附加边。Dark 有 \\(n-1\\) 条主要边，并且 Dark 的任意两个结点之间都存在一条只由主要边构成的路径。另外，Dark 还有 \\(m\\) 条附加边。

你的任务是把 Dark 斩为不连通的两部分。一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的，而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。现在你想要知道，一共有多少种方案可以击败 Dark。

注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

数据范围：\\(1\\le n\\le 10^5, 1\\le m\\le 2\\times 10^5\\)。

题解

考虑枚举第一次删掉的边是哪一条。显然这个东西最开始是一个树，每次添加一条附加边就会多加入一个环。

对于一条原先的树边，如果它不被任何一个环所包含，那么砍掉它就会将 Dark 直接分为两半，此时任意再切一个附加边即可，对答案的贡献是 \\(m\\)。若这条树边被一个环所包含（也就是这条边是某个环的组成部分），那么切了它就只能再切那条相应附加边，对答案的贡献是 \\(1\\)，若被两个或以上的包含，那么切这条边就没有任何用处。

暴力的做法是 \\(O(n^2)\\) 的，时间复杂度卡在了统计每条树边被几个环所包含。

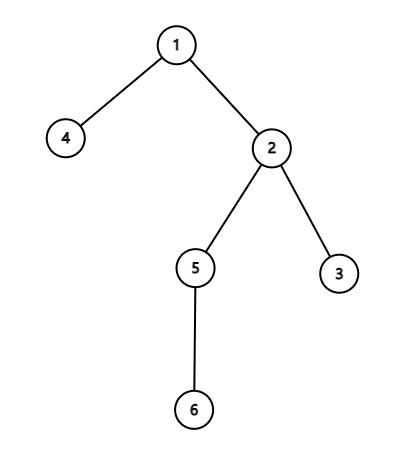
比如这个图，若在 6 与 3 之间加上了一条附加边，则会形成一个 \\(2-3-6-5\\) 的环，发现这个环其实最高只影响到了 \\(\\operatornameLCA(u,v)\\)，于是考虑树上差分，对于每条附加边 \\(u,v\\)，使得 \\(d_u,d_v\\) 都增加 \\(1\\)，\\(d_\\operatornameLCA(u,v)\\) 减 \\(2\\)。最后统计一下即可。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 5;
int n, m, d[MAXN], dep[MAXN], fa[MAXN][32], ans[MAXN], anss;
vector<int> G[MAXN];

void predfs(int x, int fat) 
  fa[x][0] = fat;
  dep[x] = dep[fat] + 1;
  for (auto u : G[x]) 
    if (u == fat) continue;
    predfs(u, x);
  


int LCA(int u, int v) 
  if (dep[u] < dep[v]) swap(u, v);
  for (int i = 29; i >= 0; --i) 
    if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
  
  if (u == v) return v;
  for (int i = 29; i >= 0; --i) 
    if (fa[u][i] != fa[v][i]) 
      u = fa[u][i], v = fa[v][i];
    
  
  return fa[u][0];


void dfs(int x, int fat) 
  ans[x] = d[x];
  for (auto u : G[x]) 
    if (u == fat) continue;
    dfs(u, x);
    ans[x] += ans[u];
  


int main(void) 
  cin >> n >> m;
  for (int i = 1; i < n; ++i) 
    int u, v;
    cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  
  // LCA Init
  predfs(1, 0);
  for (int i = 1; i < 30; ++i) 
    for (int j = 1; j <= n; ++j) 
      fa[j][i] = fa[fa[j][i - 1]][i - 1];
    
  
  // Calculate Answer
  for (int i = 1; i <= m; ++i) 
    int u, v;
    cin >> u >> v;
    d[u]++, d[v]++, d[LCA(u, v)] -= 2;
  
  dfs(1, 0);
  for (int i = 2; i <= n; ++i) 
    if (ans[i] == 0)
      anss += m;
    else if (ans[i] == 1)
      anss++;
  
  cout << anss << endl;
  return 0;

1553：例 2暗的连锁

1553：【例 2】暗的连锁

时间限制: 1000 ms         内存限制: 524288 KB

【题目描述】

原题来自：POJ 3417

Dark 是一张无向图，图中有 N个节点和两类边，一类边被称为主要边，而另一类被称为附加边。

Dark 有 N–1 条主要边，并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。

另外，Dark 还有 M条附加边。

你的任务是把 Dark 斩为不连通的两部分。

一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。

一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。

现在你想要知道，一共有多少种方案可以击败 Dark。

注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

【输入】

第一行包含两个整数 N 和 M；

之后 N–1行，每行包括两个整数 A 和 B，表示 A 和 B之间有一条主要边；

之后 M行以同样的格式给出附加边。

【输出】

输出一个整数表示答案。

【输入样例】

4 1
1 2
2 3
1 4
3 4

【输出样例】

3

【提示】

数据范围与提示：

对于 20% 的数据，1≤N,M≤100；

对于 100% 的数据，1≤N≤(1*10^{5}),1≤M≤ (2* 10^{5} )。

数据保证答案不超过 (2 ^ {31}-1)。

 

【题解】

 

考虑枚举每条主要边删掉后情况，删后原树被分为两块，若中间没有附加边，则ans+m，若有一条则只能删掉这条，若有两条以上则无解。

 

判断每条附加边对几条主要边有贡献，发现它只对他两个端点之间的路径有贡献。

 

树上差分或者树链剖分均可解决。

 

代码如下：

 

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,last[N],size,f[N][20],dep[N],cha[N];
struct pigu
{
    int dao,ne;
}a[N<<1];
inline void lingjiebiao(int x,int y)
{
    a[++size].dao=y;
    a[size].ne=last[x];
    last[x]=size;
}
inline void dfs1(int now,int fa)
{
    f[now][0]=fa;dep[now]=dep[fa]+1;
    for(int i=1;f[f[now][i-1]][i-1];i++) f[now][i]=f[f[now][i-1]][i-1];
    for(int i=last[now];i;i=a[i].ne)
    {
        if(a[i].dao==fa) continue;
        dfs1(a[i].dao,now);
    }
}
inline int get_lca(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=19;i>=0;i--) if(dep[x]-(1<<i)>=dep[y]) x=f[x][i];
    if(x==y) return x;
    for(int i=19;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
inline void dfs2(int now)
{
    for(int i=last[now];i;i=a[i].ne)
    {
        if(f[now][0]==a[i].dao) continue;
        dfs2(a[i].dao);
        cha[now]+=cha[a[i].dao];
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1,x,y;i<=n-1;i++)
    {
        scanf("%d%d",&x,&y);
        lingjiebiao(x,y);
        lingjiebiao(y,x);
    }
    dfs1(1,0);
    for(int i=1,x,y;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        int lca=get_lca(x,y);
        cha[x]++;cha[y]++;cha[lca]-=2;
    }
    dfs2(1);
    int ans=0;
    for(int i=2;i<=n;i++)
    {
        if(cha[i]==0)
            ans+=m;
        if(cha[i]==1) ans++;
    }
    cout<<ans;
}

View Code