1064 完全二叉搜索树

Posted 2023-04-21 hxss

二叉搜索树 (BST) 递归定义为具有以下属性的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
• 若它的右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值
• 它的左、右子树也分别为二叉搜索树

完全二叉树 (CBT) 定义为除最深层外的其他层的结点数都达到最大个数，最深层的所有结点都连续集中在最左边的二叉树。

现在，给定 N 个不同非负整数，表示 N 个结点的权值，用这 N 个结点可以构成唯一的完全二叉搜索树。

请你输出该完全二叉搜索树的层序遍历。

输入格式

第一行包含整数 N，表示结点个数。

第二行包含 N 个不同非负整数，表示每个结点的权值。

输出格式

共一行，输出给定完全二叉搜索树的层序遍历序列。

数据范围

1≤N≤1000,
结点权值不超过 2000。

输入样例：

10
1 2 3 4 5 6 7 8 9 0

输出样例：

6 3 8 1 5 7 9 0 2 4

代码实现：

#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
const int N=1005;
int l[N],r[N],w[N],a[N],idx;
int n,flag;
void build(int k)
    if(k>n)return;
    build(k*2);
    w[k]=a[idx++];
    build(k*2+1);

void bfs(int x)
    queue<int>q;
    q.push(x);
    while(q.size())
        int t=q.front();
        q.pop();
        if(!flag)cout<<w[t];
        else cout<<" "<<w[t];
        flag++;
        if(2*t<=n)q.push(2*t);
        if(2*t+1<=n)q.push(2*t+1);
    

int main()
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    sort(a,a+n);
    build(1);
    bfs(1);
    return 0;

 

[基础数据结构] 判断是否为完全二叉搜索树

对二叉搜索树的定义是：
一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（$1\le i\le n$）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

给出二叉搜索树的层次遍历，并判断是否为完全二叉搜索树
可以参考PTA链接

将一系列给定数字顺序插入一个初始为空的二叉搜索树（定义为左子树键值大，右子树键值小），你需要判断最后的树是否一棵完全二叉树，并且给出其层序遍历的结果。
输入格式：
输入第一行给出一个不超过20的正整数N；第二行给出N个互不相同的正整数，其间以空格分隔。
输出格式：
将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果，数字间以1个空格分隔，行的首尾不得有多余空格。第二行输出YES，如果该树是完全二叉树；否则输出NO。
输入样例1：
9
38 45 42 24 58 30 67 12 51
输出样例1：
38 45 24 58 42 30 12 67 51
YES
输入样例2：
8
38 24 12 45 58 67 42 51
输出样例2：
38 45 24 58 42 12 67 51
NO

假如我们将二叉搜索树的根节点编号为root = 1，左孩子节点的编号为root<<1，右孩子节点的编号为root<<1|1
那么说我们将得到一颗这样的树形结构（下图为完美二叉树）：

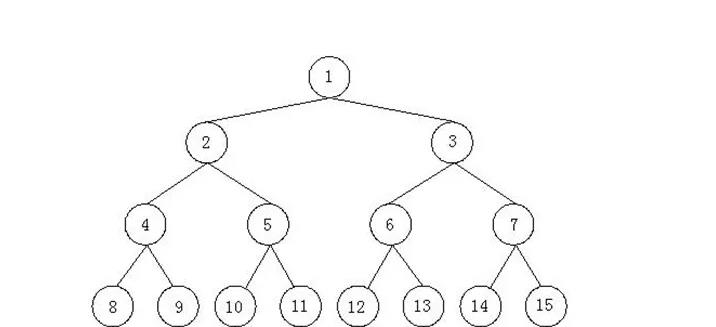
所以说在我们的存储过程中，在数组中存储一定是连续的
也就是说：我们将数组初始化为0，有值的部分一定是连续的从$1\to n$
并不可能出现$1\to n$中有的部分为0

Code:

int n,m,k;
int a[1LL<<21];
void build(int id,int x) 
	if(a[id] == 0) a[id] = x;
	else if(x > a[id]) build(id<<1,x);
	else if(x < a[id]) build(id<<1|1,x);

int main() 
	n = read;
	for(int i=1; i<=n; i++) 
		int x = read;
		build(1,x);
	
	int flag = 0;
	for(int i=1; i<=n; i++) 
		if(!a[i]) 
			flag = 1;
			break;
		
	
	if(!flag) 
		for(int i=1; i<=n; i++) 
			printf("%d%c",a[i],(i == n ? '\\n':' '));
		
	 else 
		int cnt = 0;
		for(int i=1; i; i++) 
			if(a[i]) 
				cnt ++;
				printf("%d%c",a[i],(cnt == n?'\\n':' '));
				if(cnt == n) break;
			
		
	
	printf("%s",flag?"NO":"YES");
	return 0;

/**
8
38 24 12 45 58 67 42 51

**/

阅读世界，共赴山海 423全民读书节，邀你共读