双对数坐标的两个坐标轴上的数值是啥样的对应关系?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了双对数坐标的两个坐标轴上的数值是啥样的对应关系?相关的知识,希望对你有一定的参考价值。
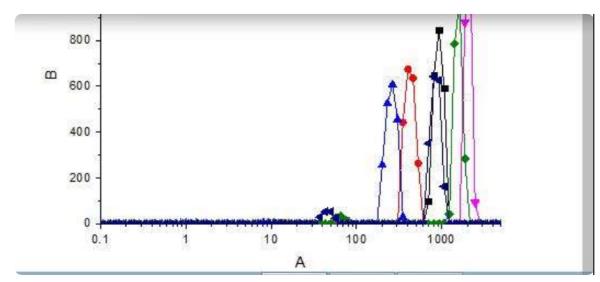
比如这张图上的

这意味着两个坐标轴是对数坐标,也就是说,如果它们对应于x和y轴,则两个轴的值等于相应的基准。
(注意:在各自的轴上是一个真实的数字,而不是对数后的值。)
例如:如果每1cm代表10次幂增加,则坐标轴刻度为1,10,100,1000,10000
扩展资料
plt.gca().invert_xaxis()#x轴反转,大的值在前面,小的值在后面
import numpy as np
import matplotlib.pyplot as plt
def Draw():
x=Freq
plt.figure(num=“Roxy,Royx,PHSxy,PHSyx曲线”)
plt.rcParams[‘font.sans-serif’]=[‘SimHei’]
plt.rcParams[‘axes.unicode_minus’]=False
plt.scatter(Freq,Roxy,marker=‘s’,alpha=0.5,c=‘r’)
plt.title(“Roxy曲线”)
plt.grid(True)
plt.loglog(x,Roxy,label=“Roxy”,color=‘r’,linewidth=1)#绘制双对数曲线
plt.gca().invert_xaxis()#x轴反转,大的值在前面,小的值在后面
plt.show()
Draw()
参考资料来源:百度百科-双对数坐标
参考技术A双对数坐标:指两个坐标轴是对数坐标,即假如对应于x、y轴,则两轴等刻度情况下,其值以相应底数成次方增长。(注意:在各自坐标轴上的是真数,不是求对数后的值。)
对数坐标系统:坐标轴是按照相等的指数增加变化表示的。
以lg α=a1+a2×lg β为例,但是这时的X、Y坐标仍然是α和 β,而不是lgα和lgβ,因为双对数曲线表示的仍然是α和 β之间的关系,而不是lgα和lgβ之间的关系。原关系式描绘出来是非线性的,不直观,而取对数后就成为线性关系。
对数坐标就是将原线性坐标标度取对数后做为坐标标度来进行绘图简化的手段。所谓双对数坐标,就是将原来两个线性坐标轴都取对数后的来的新坐标系统。

扩展资料
在下列情况下应用对数坐标纸:
1、如果所研究的函数y和自变量x在数值上均变化了几个数量级。
例如,已知x和y的数据为:x= 10, 20, 40, 60, 80, 100, 1000, 2000, 3000, 4000
y= 2, 14, 40, 60, 80, 100, 177, 181, 188, 200
在直角坐标纸上作图几乎不可能描出在x的数值等于10、20、40、60、80时,曲线开始部分的点,但是若采用对数坐标纸则可以得到比较清楚的曲线(如图3)。
2、需要将曲线开始部分划分成展开的形式。
3、当需要变换某种非线性关系为线性关系时。
4、坐标轴的梯度选取要符合对数运算法则。
参考资料来源:百度百科-双对数坐标
参考技术B双对数坐标:指两个坐标轴是对数坐标,即假如对应于x、y轴,则两轴等刻度情况下,其值以相应底数成次方增长。(注意:在各自坐标轴上的是真数,不是求对数后的值。)
对数坐标系统:坐标轴是按照相等的指数增加变化表示的。
以lg α=a1+a2×lg β为例,但是这时的X、Y坐标仍然是α和 β,而不是lgα和lgβ,因为双对数曲线表示的仍然是α和 β之间的关系,而不是lgα和lgβ之间的关系。原关系式描绘出来是非线性的,不直观,而取对数后就成为线性关系。
对数坐标就是将原线性坐标标度取对数后做为坐标标度来进行绘图简化的手段。所谓双对数坐标,就是将原来两个线性坐标轴都取对数后的来的新坐标系统。

扩展资料
在下列情况下应用对数坐标纸:
1)如果所研究的函数y和自变量x在数值上均变化了几个数量级。
例如,已知x和y的数据为:x= 10, 20, 40, 60, 80, 100, 1000, 2000, 3000, 4000
y= 2, 14, 40, 60, 80, 100, 177, 181, 188, 200 在直角坐标纸上作图几乎不可能描出在x的数值等于10、20、40、60、80时,曲线开始部分的点,但是若采用对数坐标纸则可以得到比较清楚的曲线。
2)需要将曲线开始部分划分成展开的形式。
3)当需要变换某种非线性关系为线性关系时。
4)坐标轴的梯度选取要符合对数运算法则。
参考资料来源:百度百科-双对数坐标
参考技术C双对数坐标:指两个坐标轴是对数坐标,即假如对应于x、y轴,则两轴等刻度情况下,其值以相应底数成次方增长。(注意:在各自坐标轴上的是真数,不是求对数后的值。)
举例来说:如果每1cm代表10的1次方增加,则坐标轴刻度依次为1,10,100,1000,10000……
对数坐标系统:坐标轴是按照相等的指数增加变化表示的。举例来说:如果每1cm代表10的1次方增加,则坐标轴刻度的表示依次为1,10,100,1000,10000……
算数坐标系统较对数坐标系统,他们区别体现于等刻度值增长方式不同,一个均匀增长,一个对数增长。
扩展资料
在下列情况下应用对数坐标纸:
1、如果所研究的函数y和自变量x在数值上均变化了几个数量级。
例如,已知x和y的数据为:x= 10, 20, 40, 60, 80, 100, 1000, 2000, 3000, 4000
y= 2, 14, 40, 60, 80, 100, 177, 181, 188, 200
在直角坐标纸上作图几乎不可能描出在x的数值等于10、20、40、60、80时,曲线开始部分的点,但是若采用对数坐标纸则可以得到比较清楚的曲线(如图3)。
2、需要将曲线开始部分划分成展开的形式。
3、当需要变换某种非线性关系为线性关系时。
4、坐标轴的梯度选取要符合对数运算法则。
参考资料来源:百度百科-双对数坐标
双对数坐标的两个坐标轴上的数值的对应关系:
以lg α=a1+a2×lg β为例,但是这时的X、Y坐标仍然是α和 β,而不是lgα和lgβ,因为双对数曲线表示的仍然是α和 β之间的关系,而不是lgα和lgβ之间的关系。原关系式描绘出来是非线性的,不直观,而取对数后就成为线性关系。
扩展资料:
应用对数坐标的范围:
1、如果所研究的函数y和自变量x在数值上均变化了几个数量级。
2、需要将曲线开始部分划分成展开的形式。
3、当需要变换某种非线性关系为线性关系时。
4、坐标轴的梯度选取要符合对数运算法则。
参考资料:百度百科——双对数
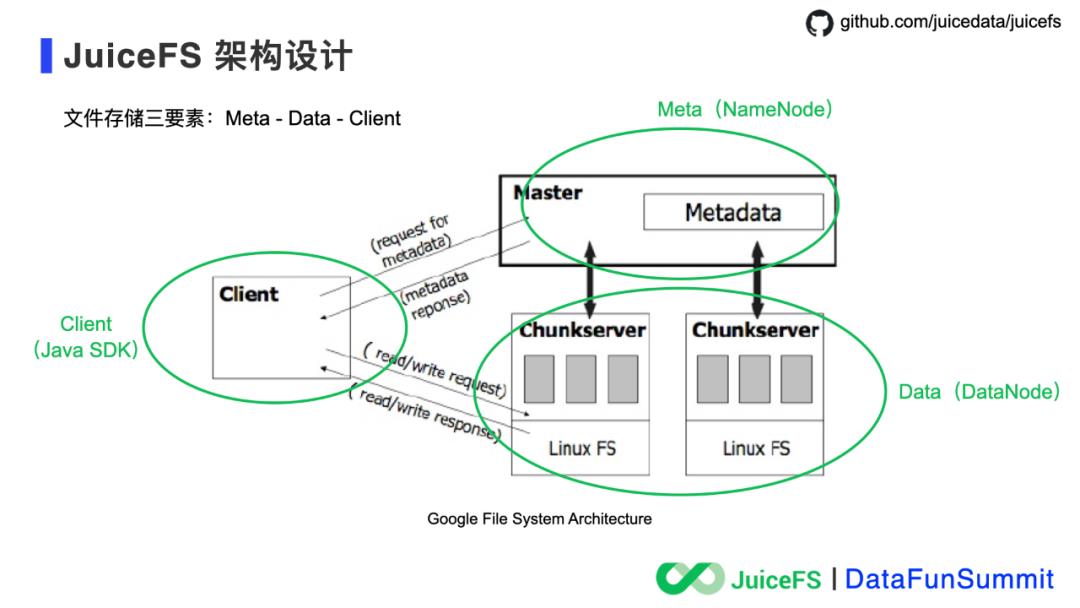
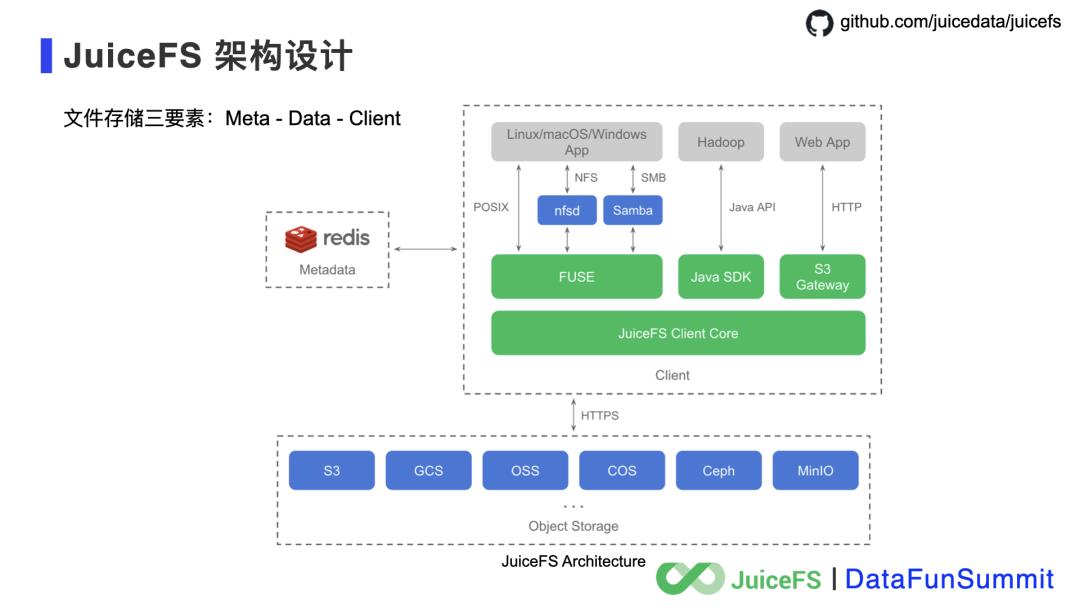
云原生时代的分布式文件系统是啥样的?
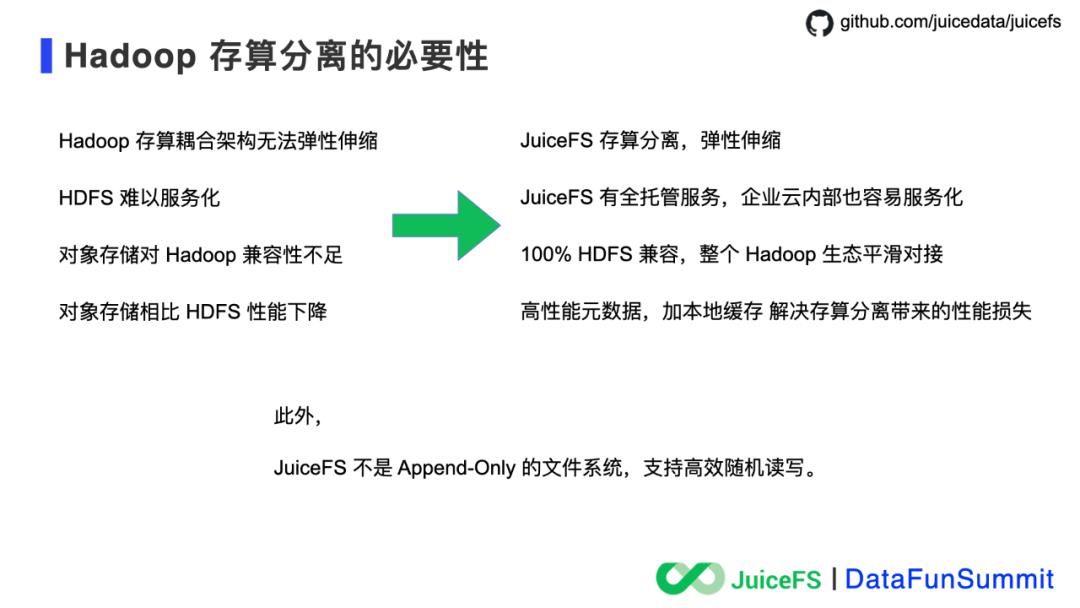
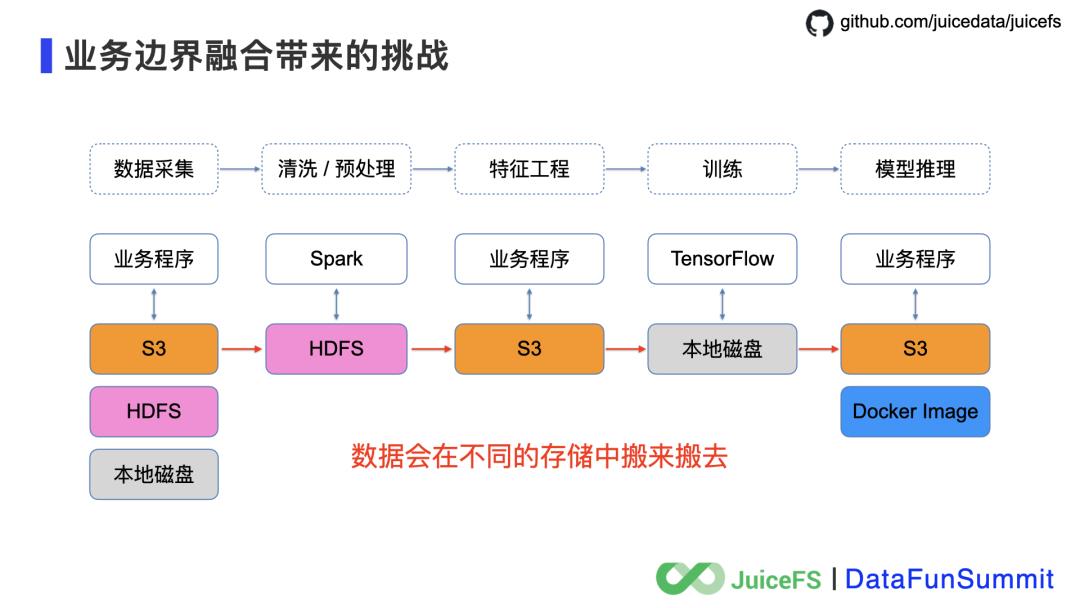
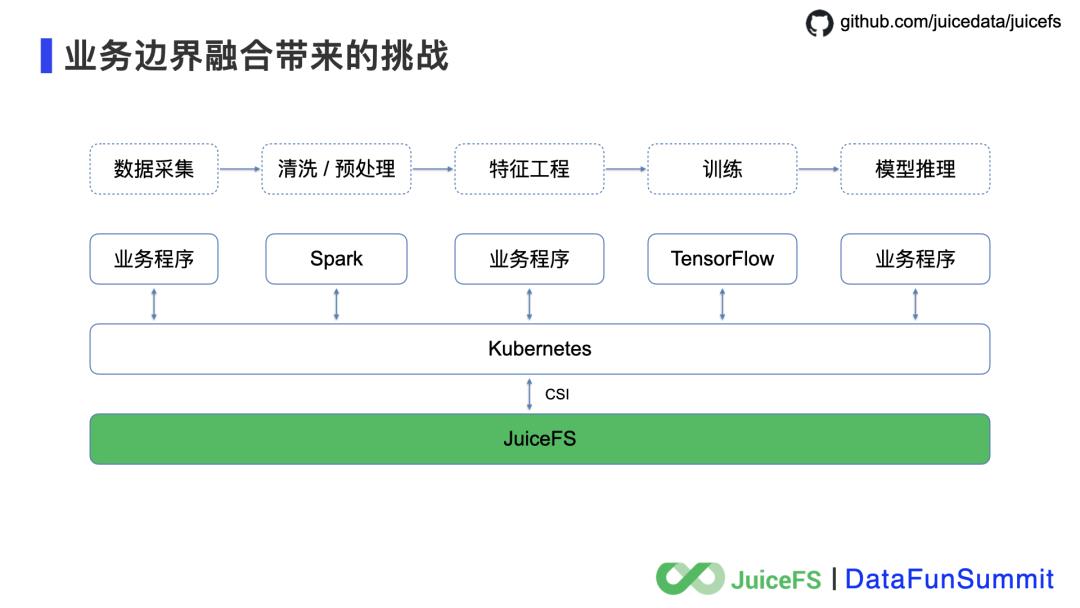
2021年全新发布 Kylin 4.0.0-beta 摒弃了旧的存储系统 HBase,转而使用 Parquet 文件格式,通过减少对 Hadoop 的依赖、使用文件作为存储,使得 Kylin 在云上的部署更加快速、低成本,更加符合云原生的技术趋势。对于云上的常见问题,即如何提升云上经常使用的对象存储的性能和成本;如何实现存储系统服务化,支持弹性伸缩;支持 Hadoop 生态、OLAP 产品等实现存储计算分离,同时具备简单、可靠、高性能、低成本等特性,其实开源社区目前已经有不少成熟的解决方案,JuiceFS 正是其中之一。
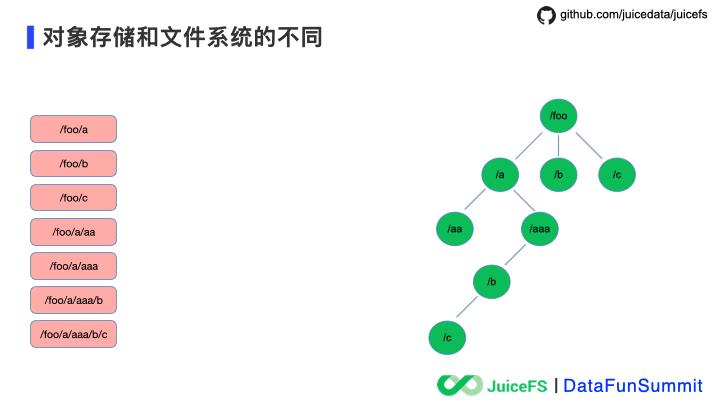
mv /foo /bar
这个改名操作中,昨天对象存储需要在元数据索引中找到搜索出所有 key 包含
/foo
对象,然后拷贝为一份新的对象,将 key 里的
/foo
改为
/bar
,这样就会有大量的对象发生 I/O 复制,拷贝完成后删除旧的对象,在拷贝和删除完成之后再更新对象存储的元数据索引。整个操作没有事务保证,完成时间依赖于改名操作涉及的对象数量,缺少事务保证也是造成数据不是强一致性的原因。


数据强一致性,这是文件系统必须的;
高性能元数据,解决对象存储在计算、分析场景中的痛点;
多访问协议互通,包括 POSIX、HDFS、S3,其实 POSIX 是最久经考验,生态丰富的文件访问接口,但是考虑到已有的 Hadoop 生态和基于 S3 API 开发的程序,JuiceFS 需要提供一个平滑对接的体验才好,不要让开发者改代码;
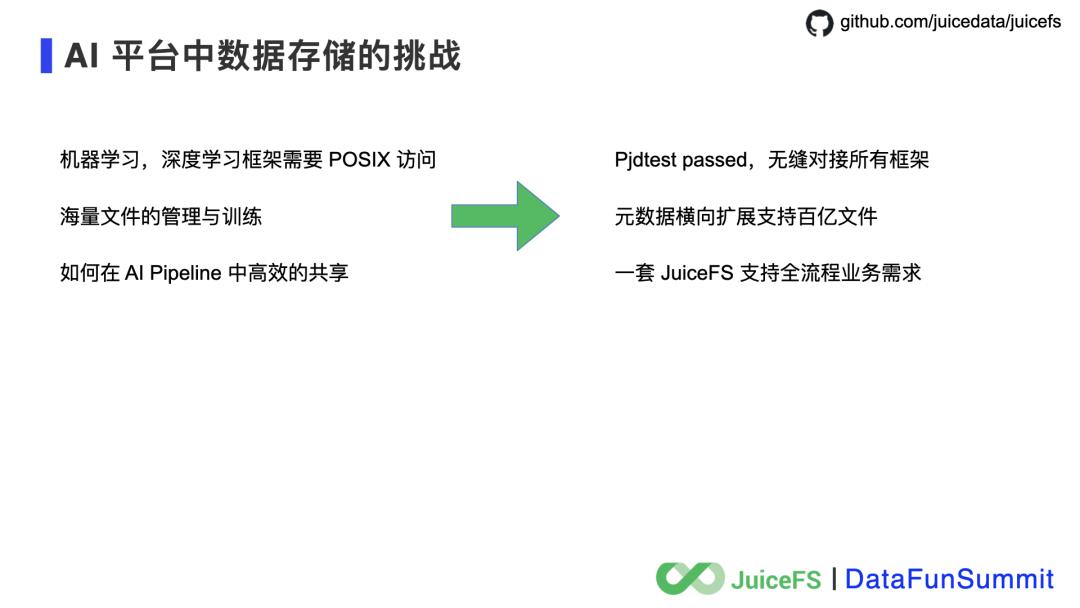
小文件管理能力,无论在大数据场景还是 AI 训练场景,十亿、百亿甚至千亿文件的管理需求被越来越多的提起。在实际的生产环境中,也已经有客户使用 JuiceFS 管理数十亿的文件了。
Kubernetes 友好,这是云原生时代最重要的用户体验,JuiceFS 必须支持,而且必须支持的很好。



近期热文推荐
以上是关于双对数坐标的两个坐标轴上的数值是啥样的对应关系?的主要内容,如果未能解决你的问题,请参考以下文章