对飞桨小汪比赛的一些思路

Posted 2023-04-19 yonuyeung

纵观各大比赛，常见的打榜技巧如下

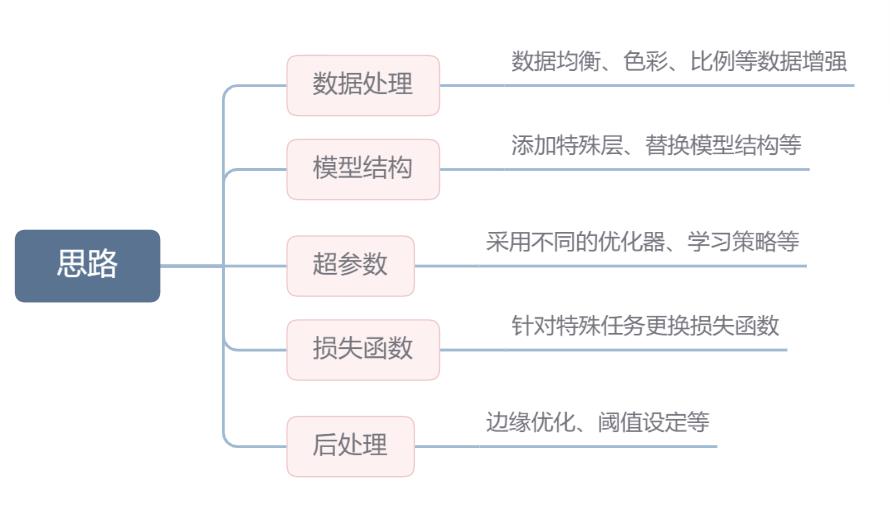
 针对每一点思路，我首先对他们进行详细的解释，再针对飞桨小汪这个比赛做出一些具体的上分策略

详细解释

思路1：数据处理

1. 数据增强：使用数据增强技术可以增加数据的多样性和数量，从而提高模型的鲁棒性和泛化能力。例如，可以进行镜像翻转、随机裁剪、旋转、缩放、变形等操作。

2. 数据预处理：在输入模型之前，需要对图像进行一些预处理操作，如图像归一化、尺寸调整等。这有助于减少模型训练的时间和提高模型性能。

3. 数据采样：在训练过程中，数据不平衡是一个常见的问题。一些类别可能比其他类别出现更少。因此，可以使用数据采样技术来平衡数据，如过采样、欠采样、SMOTE等。

4. 数据筛选：对于图像目标检测和语义分割，需要标注每个像素的标签，这个过程需要耗费大量的时间和人力。因此，可以通过一些筛选技术，如基于聚类的方法、基于众包的方法等，来减少标注数据的工作量。

5. 数据集合并：如果存在多个数据集，可以将它们合并成一个更大的数据集，这有助于增加数据量和多样性，提高模型的性能。

6. 数据格式转换：在模型训练过程中，需要将图像数据转换为模型可以处理的格式，如TensorFlow的TFRecord格式等。这个转换过程可以优化读取速度和训练速度。

7. 数据分布式处理：如果数据量非常大，可以使用分布式处理技术来加快数据处理速度，如使用Spark、Hadoop等分布式处理框架。

8. 数据清洗和预处理：可以使用自动化工具进行数据清洗和预处理，如使用OpenCV进行图像预处理，使用图像标注工具来标注数据等。

思路2：模型结构

1. Backbone架构的选择：选择合适的Backbone架构可以提高模型的性能。例如，ResNet、VGG、Inception、MobileNet等经典的CNN网络都可以作为Backbone。

2. 网络宽度和深度的调整：增加网络宽度和深度可以提高模型的性能，但也会增加模型的参数量和计算量。因此，需要根据实际应用情况进行调整。

3. 特征金字塔：对于不同尺度的特征，可以采用特征金字塔的方法来提高模型性能。例如，Faster R-CNN模型使用金字塔网络来提取不同尺度的特征。

4. 多尺度融合：对于语义分割模型，可以使用多尺度融合的方法来获得更好的语义信息。例如，PSPNet和DeepLab v3+等模型就采用了多尺度融合的方法。

5. 上采样方法：在语义分割模型中，需要将低分辨率的特征图上采样到原图尺寸，这需要使用一些上采样方法，如双线性插值、反卷积、空洞卷积等。

6. 非局部注意力机制：在模型中加入非局部注意力机制可以提高模型的性能。例如，SENet模型中使用了一种非局部注意力机制来提取特征。

7. 注意力机制：注意力机制可以帮助模型更好地关注重要的区域。例如，Mask R-CNN模型中使用了注意力机制来帮助定位目标。

8. 端到端的训练：将不同组件（如Backbone、特征提取器、检测器等）组合成一个端到端的模型可以提高模型的性能和效率。

思路3：超参数

1. 学习率调度：学习率是训练深度学习模型时最重要的超参数之一。合适的学习率可以提高模型的训练速度和性能。可以采用动态调整学习率的方法，如余弦退火、多步调度等。

2. Batch Size的选择：Batch Size决定了在每个训练迭代中使用多少样本进行训练。较大的Batch Size可以加速模型训练，但也会占用更多内存。在选择Batch Size时，需要平衡模型性能和资源利用率。

3. 权重衰减：权重衰减是一种正则化方法，可以防止模型过拟合。合适的权重衰减可以提高模型的性能。

4. Dropout：Dropout是一种正则化方法，可以随机删除神经元。合适的Dropout可以提高模型的性能。

5. 激活函数的选择：合适的激活函数可以提高模型的性能。例如，在目标检测和语义分割模型中，常用的激活函数有ReLU、LeakyReLU等。

6. Anchor尺寸的设置：在目标检测模型中，Anchor是指预定义的一组边界框，用于检测目标。合适的Anchor尺寸可以提高模型的性能。

7. 网络层数的选择：网络层数的选择可以影响模型的性能。在深度网络中，较深的网络可以提高模型的表达能力，但也会增加计算量。

8. 梯度裁剪：梯度裁剪可以帮助防止梯度爆炸问题。合适的梯度裁剪可以提高模型的性能。

9. 数据增强：数据增强是一种有效的正则化方法，可以增加数据集的多样性。在目标检测和语义分割模型中，可以使用随机裁剪、缩放、旋转、翻转等方法进行数据增强。

思路4：损失函数

1. Focal Loss：Focal Loss是一种损失函数，可以帮助解决类别不平衡问题。在目标检测和语义分割中，经常会遇到类别不平衡的情况，Focal Loss可以帮助提高模型对少数类别的识别能力。

2. Dice Loss：Dice Loss是一种损失函数，用于分割任务中。它可以帮助模型更好地处理类别边界模糊的情况，提高模型的分割精度。

3. IoU Loss：IoU Loss是一种损失函数，用于分割任务中。它可以帮助模型更好地处理类别边界模糊的情况，提高模型的分割精度。

4. Smooth L1 Loss：Smooth L1 Loss是一种损失函数，用于目标检测中。它可以提高模型对目标框的回归精度，同时减少对噪声数据的敏感度。

5. Cross Entropy Loss：Cross Entropy Loss是一种常用的分类损失函数，可以用于目标检测和语义分割中。它可以帮助模型更好地处理多分类问题。

6. Binary Cross Entropy Loss：Binary Cross Entropy Loss是一种常用的二分类损失函数，可以用于目标检测和语义分割中。它可以帮助模型更好地处理二分类问题。

7. KLDiv Loss：KLDiv Loss是一种损失函数，用于目标检测和语义分割中。它可以帮助模型更好地处理类别不平衡问题，提高模型的分类精度。

思路5：后处理

1. 非极大值抑制（NMS）：在目标检测任务中，NMS是一种常用的后处理技巧，用于剔除多余的重叠框，保留最优的检测结果。NMS的优化方法包括设置阈值、调整IoU重叠度等。

2. 分割后处理：在语义分割任务中，分割后处理可以帮助提高分割精度。例如，可以使用形态学运算进行图像处理，填补小的空洞和孔洞，去除边缘噪声等。

3. 后处理策略的优化：对于不同的目标检测和语义分割模型，可以根据模型输出的特点和需求，选择不同的后处理策略。例如，可以根据实际应用场景和需求，选用不同的NMS方法，或者设置不同的分割阈值等。

4. 模型融合：在实际应用中，可以通过模型融合的方式，将多个目标检测和语义分割模型的结果进行融合，从而进一步提高模型的性能和效率

 

针对此次比赛的一些优化思路

LeetCode笔记：Weekly Contest 241 比赛记录

• LeetCode笔记：Weekly Contest 241
  • 0. 赛后总结
  • 1. 题目一
    • 1. 解题思路
    • 2. 代码实现
  • 2. 题目二
    • 1. 解题思路
    • 2. 代码实现
  • 3. 题目三
    • 1. 解题思路
    • 2. 代码实现
  • 4. 题目四
    • 1. 解题思路
    • 2. 代码实现

0. 赛后总结

如上一个博客所述，这周的比赛其实因为一些琐事没能参加，只是赛后做了一下比赛的题目，这里就大致记录一下吧。

1. 题目一

给出题目一的试题链接如下：

• 1863. Sum of All Subset XOR Totals

1. 解题思路

这一题我的解法其实很暴力，就是彻底的暴力求解，把所有的$2^n$种可能性全部计算一下，然后就能够得到最终的答案了。

2. 代码实现

给出python代码实现如下：

class Solution:
    def subsetXORSum(self, nums: List[int]) -> int:
        n = len(nums)
        res = 0
        for item in product(range(2), repeat=n):
            s = 0
            for flag, k in zip(item, nums):
                if flag == 1:
                    s = s ^ k
            res += s
        return res

提交代码评测得到：耗时148ms，占用内存14MB。

2. 题目二

给出题目二的试题链接如下：

• 1864. Minimum Number of Swaps to Make the Binary String Alternating

1. 解题思路

这一题我这边的思路其实也挺暴力的，要能够完成这种变换，那么0和1的数目就必须满足差值最多只能为1，然后最终的字符排列就是确定的，由此，我们统计一下原始字符串与最终目标字符串之间的差异字符数目就可以最终给出需要交换的次数。

2. 代码实现

给出python代码实现如下：

class Solution:
    def minSwaps(self, s: str) -> int:
        cnt = Counter(s)
        def count_diff(s1, s2):
            cnt = 0
            for c1, c2 in zip(s1, s2):
                if c1 != c2:
                    cnt += 1
            return cnt // 2
        
        if abs(cnt["0"] - cnt["1"]) > 1:
            return -1
        elif cnt['0'] == cnt['1'] + 1:
            return count_diff("0" + "10" * (len(s) // 2), s)
        elif cnt["0"] == cnt['1'] - 1:
            return count_diff("1" + "01" * (len(s) // 2), s)
        else:
            return min(count_diff("10" * (len(s) // 2), s), count_diff("01" * (len(s) // 2), s))

提交代码评测得到：耗时24ms，占用内存14.3MB。

3. 题目三

给出题目三的试题链接如下：

• 1865. Finding Pairs With a Certain Sum

1. 解题思路

这一题我给出的结构其实不算多么巧妙，就是用两个字典结构保存nums1和nums2，然后为了保留index信息，在单独保存一下nums2，然后后面的add操作的算法复杂度就是$O(1)$，然后count的算法复杂度就是$O(N_1)$。

2. 代码实现

给出python代码实现如下：

class FindSumPairs:

    def __init__(self, nums1: List[int], nums2: List[int]):
        self.nums1_cnt = Counter(nums1)
        self.nums1_elems = sorted(self.nums1_cnt.keys())
        self.nums2 = nums2
        self.nums2_cnt = Counter(nums2)
        

    def add(self, index: int, val: int) -> None:
        x = self.nums2[index]
        self.nums2_cnt[x] -= 1
        self.nums2[index] += val
        self.nums2_cnt[x+val] += 1

    def count(self, tot: int) -> int:
        res = 0
        for k in self.nums1_elems:
            if k >= tot:
                break
            res += self.nums1_cnt[k] * self.nums2_cnt[tot-k]
        return res

提交代码评测得到：耗时816ms，占用内存44.4MB。

4. 题目四

给出题目四的试题链接如下：

• 1866. Number of Ways to Rearrange Sticks With K Sticks Visible

1. 解题思路

这次的第四题坦率地说有点一言难尽，怎么说呢，思路一开始就很明确，就是动态规划，然后就是考虑递推公式，然后就是想了一下午都没有想出来，但是看了一下答案之后发现简直简单的离谱，原因就是换个角度思考问题就行。

我们先给出递推公式如下：
$$f(n,k)=f(n-1.k-1)+(n-1)\times f(n-1,k)$$

其中，$f(n,k)$的定义就是题目中的定义，就是n个数，然后可见的数为k个。

但是，我们考察迭代公式的时候，不要去考虑加入一个最大的数，而是应该考虑将原始的排列中所有的数字加1，然后加入一个最小的数，此时，需要考虑的前一种$k$的可能性只能为$k$或者$k-1$，我们分别这两种情况：

1. 如果原来暴露的数刚好就是k个时，我们能够加入的位置就一定是除了第一个位置之外所有的位置，所以此时的排列数目就是$(n-1)\times f(n-1,k)$；
2. 如果原来暴露的数目为k-1时，此时我们就必须将这个最小数加入到第一个数的位置，此时的所有可能性为：$f(n-1,k-1)$。

结合上述两种情况，我们即可得到最终的递推公式。

2. 代码实现

给出python代码实现如下：

class Solution:
    def rearrangeSticks(self, n: int, k: int) -> int:
        MOD = 10**9+7
        
        dp = [[0 for _ in range(k+1)] for _ in range(n+1)]
        dp[1][1] = 1
        for i in range(n):
            for j in range(min(k, i+1)):
                if i == 0 and j == 0:
                    continue
                dp[i+1][j+1] = (dp[i][j] + i * dp[i][j+1]) % MOD
                
        return dp[n][k]

提交代码评测得到：耗时2548ms，占用内存38.6MB。