Search是数据结构中最基础的应用之一了，在python中，search有一个非常简单的方法如下：
15 in [3,5,4,1,76]
False
不过这只是search的一种形式，下面列出多种形式的search用做记录：
一、顺序搜索
顺着list中的元素一个个找，找到了返回True，没找到返回False
def sequential_search(a_list, item):
pos = 0
found = False
while pos < len(a_list) and not found:
if a_list[pos] == item:
found = True
else:
pos = pos+1
return found
test_list = [1, 2, 32, 8, 17, 19, 42, 13, 0]
print(sequential_search(test_list, 3))
print(sequential_search(test_list, 13))
False
True
顺序排序的时间复杂度如下表，最好和最坏的情况下的时间复杂度分别是O(1)和O(n)，分别对应要找的元素在list中的第一个和最后一个。对于平均情况来说，计算方法为(1+2+3+...+n)/n = (1+n)/2，所以其时间复杂度为O(n/2)
看到上面的图，item存在与不存在平均情况的时间复杂度是不一样的。因为如果不存在的话，search必须每次都把所有元素都遍历完毕才行，所以平均时间复杂度是O(n)。
但是对于原本list里的元素就是有序排列(ordered list)的情况来说，情况就不一样了。因为元素是顺序排列，所以一旦找到比他小和比他大的两个连接元素，就可以直接得出结论返回False，所以平均时间复杂度是O(n/2)
有序排列时时间复杂度表格如下：
def ordered_sequential_search(a_list, item):
pos = 0
found = False
stop = False
while pos < len(a_list) and not found and not stop:
if a_list[pos] == item:
found = True
else:
if a_list[pos] > item:
stop = True
else:
pos = pos+1
return found
test_list = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(ordered_sequential_search(test_list, 3))
print(ordered_sequential_search(test_list, 13))
False
True
二、二分搜索
首先明确一点，二分搜索也是对于ordered list来说的。
顺序搜索是从头一个个往下找，而对于ordered list来说，二分搜索先检阅list中的中间元素，比较其与我们需要找的item的大小，再确定item所属的左右区域，接着进行一个简单的递归（recursion），直到找到所属的item或者递归的list只剩下一个元素。
首先，用迭代（iteration）解决这个问题：
def binary_seach(a_list, item):
first = 0
last = len(a_list)-1
found = False
while first < last and not found:
midpoint = (first+last)//2
if a_list[midpoint]==item:
found = True
else:
if item < a_list[midpoint]:
last = midpoint-1
else:
first = midpoint+1
return found
然后，用递归（recursion）再解决这个问题：
def binary_search(a_list, item):
if len(a_list)==0: # 对于递归（recursion）来说，最开始一定要给出结束的条件
return False
else:
midpoint = len(a_list) // 2
if a_list[midpoint]==item:
found = True
else:
if item < a_list[midpoint]: # 时间都消耗在了这个语句上
return binary_search(a_list[:midpoint-1], item)
else:
return binary_search(a_list[midpoint+1:], item)
return found
test_list = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(test_list, 3))
print(binary_search(test_list, 13))
False
True
二分搜索的时间复杂度： 对于这个算法，时间消耗都花在了比较元素大小上，每一次元素的比较都让我们少了一半的list，当list的长度为n时，我们可以用来比较的次数只有log(n)次，对于这个解释，我更想拿出《算法导论》中的这个图出来，简直明了。
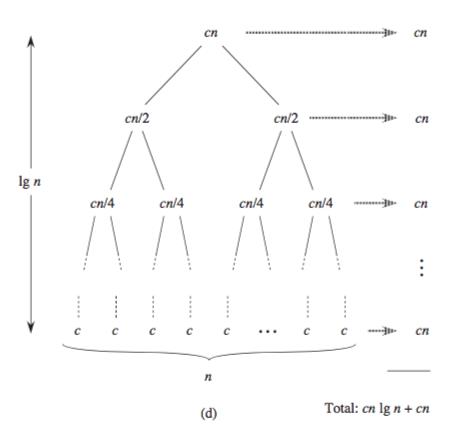
这是一个用于分治策略（divide-and-conquer）的图，但是放在这里也有助于理解，每一次元素的比较相当于这个树又多了一层，比较的次数即为树的层数。
当然，所有的这一切是在不考虑python中list的slice的操作时间的情况下。实际上，slice的操作时间复杂度应该是O(k)的，理论上来说二分搜索消耗的不是严格的log时间。
PS: 二分算法需要先将list进行排序，实际上，在list长度很小的情况下，排序的操作消耗的时间可能根本不值得。这个时候，直接用顺序搜索的方法可能更高效。
三、哈希（hash）搜索
基本思想： 如果我们事先知道一个元素本来应该在的地方，那我们就可以直接找到他了。
哈希表（hash table，也叫散列表）就是这样运作的。如下图所示，该哈希表有m=11个槽（slot），每个槽有其对应的name（0,1,2,....10），每个槽可空可满，空的时候填充None，槽和各个元素的映射（mapping）是由哈希函数（hash function）来决定的，假设我们有整数元素54,26,93,17,77,31需要放入哈希表中，我们可以使用哈希函数h(item) = item%11来决定槽的name，函数中的11表示哈希表的长度。
一旦我们将元素放入进哈希表中，如下图，我们就可以计算此哈希表的装载率（load factor）λ = number_of_item / table_size。对于下表来说，装载率为6/11。
敲黑板！ 当我们要搜索一个item的时候，我们只需要将这个item应用于哈希函数，算出该item对应在哈希表中的name，然后找到哈希表中对应name的槽的元素后进行比较。这个搜索过程的时间复杂度为O(1)。
冲突（collisions）： 如果整数集有44和22两个数，这两个数除以11取余都是0，那么就会产生放置冲突。
3.1 哈希函数选择
选择哈希函数的主要目的就是减少冲突的出现。
- The division method
h(k) = k mod m
- The multiplication method
h(k) = m(k*A mod 1) 这个结果要向下取整
kA mod 1表示k*A的小数部分
还有以下两种：
The folding method for constructing hash functions begins by dividing the item into equal- size pieces (the last piece may not be of equal size). These pieces are then added together to give the resulting hash value. For example, if our item was the phone number 436-555- 4601, we would take the digits and divide them into groups of 2 (43, 65, 55, 46, 01). After the addition, 43 + 65 + 55 + 46 + 01, we get 210. If we assume our hash table has 11 slots, then we need to perform the extra step of dividing by 11 and keeping the remainder. In this case 210%11 is 1, so the phone number 436-555-4601 hashes to slot 1. Some folding methods go one step further and reverse every other piece before the addition. For the above example, we get 43 + 56 + 55 + 64 + 01 = 219 which gives 219%11 = 10.
Another numerical technique for constructing a hash function is called the mid-square method. We first square the item, and then extract some portion of the resulting digits. For ex- ample, if the item were 44, we would first compute 442 = 1, 936. By extracting the middle two digits, 93, and performing the remainder step, we get 5 (93%11). Table 5.5 shows items under both the remainder method and the mid-square method. You should verify that you understand how these values were computed.
PS: 哈希表并没有成为储存和搜索的主流。尽管哈希表搜索的时间复杂度为O(1)。这是因为如果哈希函数太复杂的话，计算槽的name花费的时间就很长了，效率也就变低了。
3.2 冲突（collision）解决
- 开放寻址（open addressing）和线性探测（linear probing）
当我们需要放到哈希表中的数为 54, 26, 93, 17, 77, 31, 44, 55, 20)时，且哈希函数为h(item)=item%11。可以看到，数77，44，55的name都是0。那么当我们放置44的时候，由于槽0已经被77占据，那么我们就依据线性探测将44放入下一个槽的位置(slot by slot)，如果依旧是填满的，则仍往下直到找到一个空的槽。按照这个逻辑，44放入槽1，55放入槽2。此方法rehash的公式：rehash(pos) = (pos + 1)%size_of_table。
但是这样的话，最后一个数20应该是放在槽9的，但是由于槽9已经满了，且之后的槽10，0，1，2都已经满了，则20只能放入槽3的位置上。
一旦我们构建了这样的哈希表，当要寻找的时候，我们根据给定的哈希函数计算出item的name，如果在槽name的位置没有找到，则继续往下一个槽找，直到找到item返回True或者直到碰到一个空的槽返回False。
不过，这样的话会带来一个问题，那就是元素聚集(clustering)，就如我们刚才的例子，所有的元素都堆积在槽0的周围，这会导致很多元素在放置的时候都会冲突然后使用线性探测来向后移位，虽在这在技术上是可行的，但是严重降低了效率。
解决clustering的一个方法那就是增加探测（probing）的距离，比如说我们在放置44的时候，并不是放置在槽0的后一个槽1，而是放在槽3，我们可以把这个规则定义为"plus 3"prob。rehash的公式改变为rehash(pos) = (pos + 3)%size_of_table
更有甚者，我们可以把这个step定为可变的二次数（h+1, h+4, h+9, h+16 ...）
- Chaining
第二种方法就是在冲突的槽上创建一个链表，如下图所示：
优点：由于每个槽中都储存该槽对应的元素，所以此方法的效率更高。
3.3 代码构建
下列python代码使用两个list来创建一个哈希表。一个list储存所有槽中的item的key值（由于这里的item使用的是string类型，所以需要转化成整型，对应于key），另一个平行的list储存对应的data。
it is important that the size of hash table be a prime number(质数) so that the collision resolution algorithm can be as efficient as possible.
class HashTable:
def __init__(self):
self.size = 11
self.slots =[None]*self.size
self.data = [None]*self.size
put(key, data)函数代表放置元素进槽的过程，主要部分为解决冲突的过程
def put(self, key, data):
hash_value = self.hash_function(key,len(self.slots))
if self.slots[hash_value] == None:
self.slots[hash_value] = key
self.data[hash_value] = data
else:
if self.slots[hash_value] == key:
self.data[hash_value] = data #replace
else:
next_slot = self.rehash(hash_value, len(self.slots))
while self.slots[next_slot] != None and self.slots[next_slot] != key:
next_slot = self.rehash(next_slot, len(self.slots))
if self.slots[next_slot] == None:
self.slots[next_slot] = key
self.data[next_slot] = data
else: # self.slots[next_slot] == key
self.data[next_slot] = data #replace
def hash_function(self, key, size):
return key % size
def rehash(self, old_hash, size):
return (old_hash+1) % size
get(key)函数表示取出的过程。
def get(self, key):
start_slot = self.hash_function(key, len(self.slots))
data = None
stop = False
found = False
position = start_slot
while self.slots[position] != None and not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position = self.rehash(position, len(self.slots))
if position == start_slot: #遍历完所有槽
stop = True
return data
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key, data)
__getitem__()对于我这个小白还是有点难理解的，这里引用廖雪峰的教程相应的内容：
类似
__xxx__的属性和方法在Python中都是有特殊用途的，比如__len__方法返回长度。在Python中，如果你调用len()函数试图获取一个对象的长度，实际上，在len()函数内部，它自动去调用该对象的__len__()方法
要表现得像list那样按照下标取出元素，需要实现
__getitem__()方法
与之对应的是
__setitem__()方法，把对象视作list或dict来对集合赋值
当然，对于上述操作，还有一个问题需要解决，那就是如何实现string于int之间的转化。这点其实python给出了一个ord()函数
ord(): 它以一个字符（长度为1的字符串）作为参数，返回对应的 ASCII 数值
def hash(a_string):
key = 0
for pos in range(len(a_string)):
key = key + ord(a_string[pos])
return key
Example：
h=HashTable()
data = [\'bird\',\'dog\',\'goat\',\'chicken\',\'lion\',\'tiger\',\'pig\',\'cat\']
keys = []
for animal in data:
keys.append(hash(animal))
print(keys)
[417, 314, 427, 725, 434, 539, 320, 312]
for i,key in enumerate(keys):
h[key] = data[i]
print(h.slots)
print(h.data)
[725, 539, 320, None, 312, 434, 314, None, None, 427, 417]
[\'chicken\', \'tiger\', \'pig\', None, \'cat\', \'lion\', \'dog\', None, None, \'goat\', \'bird\']
对于成功找到和未找到的时间复杂度是显然不一样的。
对于成功找到的情况，采用线性探索策略的哈希表的平均时间复杂度为：\\(\\frac{1}{2}(1+\\frac{1}{(1-\\lambda)})\\)
对于未成功找到的情况时间复杂度为：
\\(\\frac{1}{2}(1+\\frac{1}{(1-\\lambda)^{2}})\\)
如果我们应用带chaining的哈希表，成功搜索的时间复杂度为： 以上是关于Python数据结构应用4——搜索（search）的主要内容，如果未能解决你的问题，请参考以下文章 SharePoint图说搜索服务Search Service详细配置 [FreeCodeCamp笔记] Python 数据结构和算法1 二分搜索 Binary Search [FreeCodeCamp笔记] Python 数据结构和算法1 二分搜索 Binary Search [FreeCodeCamp笔记] Python 数据结构和算法1 二分搜索 Binary Search
\\(1 + \\frac{