Python中的turtle初探

Posted 2020-11-02 Byron NG

turtle

Python自带了一个turtle库，就像名字turtle说的那样，你可以创建一个turtle，然后这个turtle可以前进，后退，左转，这个turtle有一条尾巴，能够放下和抬起，当尾巴放下的时候，turtle走过的地方就留下了痕迹，也就是这只画笔的原理。

下面的表格是基本的一些turtle的方法，这里简单列举了一点。

命令	解释
turtle.Screen()	返回一个singleton object of a TurtleScreen subclass
turtle.forward(distance)	向当前画笔方向移动distance像素长
turtle.backward(distance)	向当前画笔相反方向移动distance像素长度
turtle.right(degree)	顺时针移动degree°
turtle.left(degree)	逆时针移动degree°
turtle.pendown()	移动时绘制图形,缺省时也为绘制
turtle.goto(x,y)	将画笔移动到坐标为x,y的位置
turtle.penup()	移动时不绘制图形,提起笔，用于另起一个地方绘制时用
turtle.speed(speed)	画笔绘制的速度范围[0,10]整数
turtle.circle()	画圆,半径为正(负),表示圆心在画笔的左边(右边)画圆

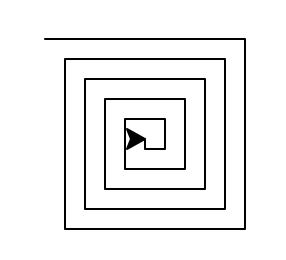
下面是一个很简单的turtle的例子，我们使用turtle来画一个螺旋的图案，这个函数采用递归的方法，每次递归的画笔减小了5个单位长度，进而形成了一个向内螺旋的图案。

import turtle

my_turtle = turtle.Turtle()
my_win = turtle.Screen()

def draw_spiral(my_turtle, line_len):
    if line_len > 0 :
        my_turtle.forward(line_len)  # turtle前进
        my_turtle.right(90)   # turtle向右转
        draw_spiral(my_turtle, line_len - 5) #turtle继续前进向右转
draw_spiral(my_turtle, 100)
my_win.exitonclick()

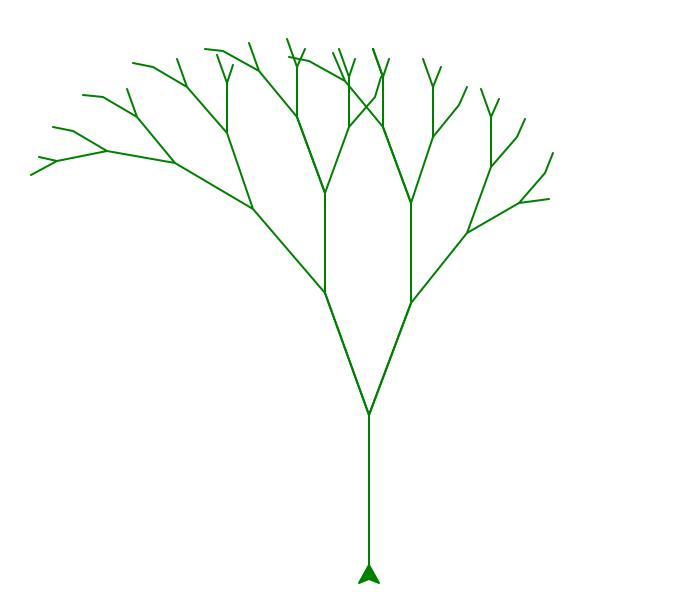
画一颗树

接下来，我们用turtle来画一颗树。过程是这样的：
branch_len为树枝的长度，这里的turtle也是采用递归的方法，在树枝需要分叉的地方建立一颗新的子树，而且是左右两颗子树，右子树的长度比左子树的长度要少5个单位。

import turtle

def tree(branch_len, t):
    if branch_len > 5:
        t.forward(branch_len)
        t.right(20)
        tree(branch_len - 15, t)
        t.left(40)
        tree(branch_len - 10, t)
        t.right(20)
        t.backward(branch_len)

def main():
    t = turtle.Turtle()
    my_win = turtle.Screen()
    t.left(90)
    t.up()
    t.backward(100)
    t.down()
    t.color("green")
    tree(75, t)
    my_win.exitonclick()
main()

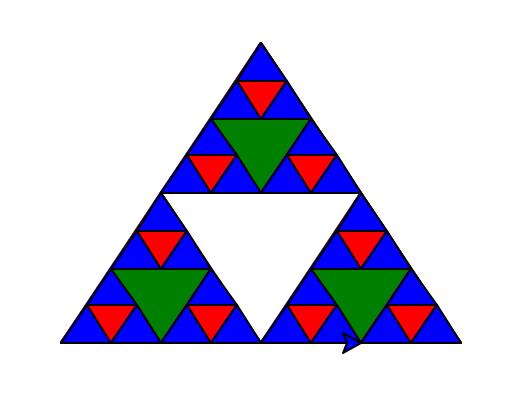
谢尔宾斯基三角形

The Sierpinski triangle illustrates a three-way recursive algorithm. The procedure for drawing a Sierpinski triangle by hand is simple. Start with a single large triangle. Divide this large triangle into four new triangles by connecting the midpoint of each side. Ignoring the middle triangle that you just created, apply the same procedure to each of the three corner triangles

import turtle
def draw_triangle(points, color, my_turtle):
    my_turtle.fillcolor(color)
    my_turtle.up()
    my_turtle.goto(points[0][0],points[0][1])
    my_turtle.down()
    my_turtle.begin_fill()
    my_turtle.goto(points[1][0], points[1][1])
    my_turtle.goto(points[2][0], points[2][1])
    my_turtle.goto(points[0][0], points[0][1])
    my_turtle.end_fill()
def get_mid(p1, p2):
    return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)
def sierpinski(points, degree, my_turtle):
    color_map = [\'blue\', \'red\', \'green\', \'white\', \'yellow\',
            \'violet\', \'orange\']
    draw_triangle(points, color_map[degree], my_turtle)
    if degree > 0:
        sierpinski([points[0],
                  get_mid(points[0], points[1]),
                  get_mid(points[0], points[2])],
              degree-1, my_turtle)
        sierpinski([points[1],
                  get_mid(points[0], points[1]),
                  get_mid(points[1], points[2])],
              degree-1, my_turtle)
        sierpinski([points[2],
                  get_mid(points[2], points[1]),
                  get_mid(points[0], points[2])],
              degree-1, my_turtle)
def main():
    my_turtle = turtle.Turtle()
    my_win = turtle.Screen()
    my_points = [[-100, -50], [0, 100], [100, -50]]
    sierpinski(my_points, 3, my_turtle)
    my_win.exitonclick()
main()

• Reference:

1. 10 分钟轻松学会 Python turtle 绘图
2. Problem Solving with Algorithms and Data Structures, Release 3.0