第6节 勒贝格积分的几何意义,富比尼定理

Posted 2023-04-18 mengqing80

第6节主要内容

学习目标:掌握直积,截面的定义和截面定理;掌握下方图形的定义与勒贝格积分的几何意义;掌握富比尼定理.

数学基础篇--详解人工智能之数学 积分学，概率空间，大数定律和中心极限定理

一、前述

上一篇我们讲到了微分学，本文我们接着讲解积分学，以及概率的相关知识。

二、本节常用符号如下。

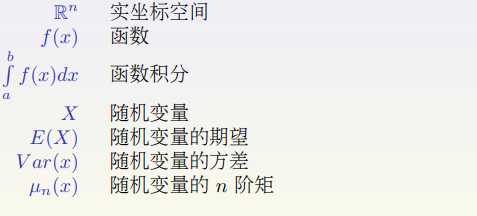
三、积分

1、积分定义

将一个函数对应的区间n等分，然后加和求极限。

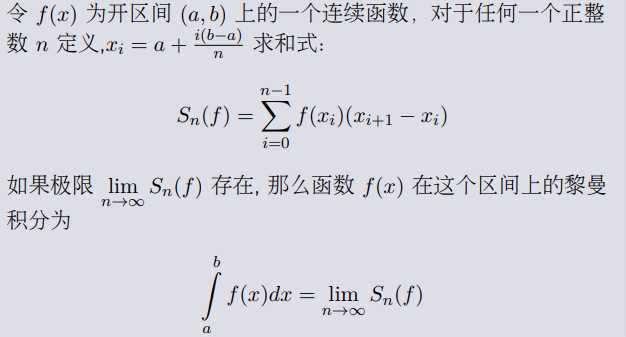
2、积分理解

代数意义: 无穷求和

几何意义: 函数与 X 轴之间的有向面积。

3、(牛顿-莱布尼茨公式)

如果 f(x) 是定义在闭区间 [a, b] 上的可微函数, 那么就有

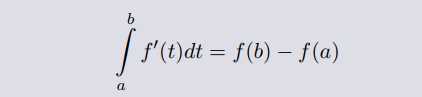
不定积分表示为

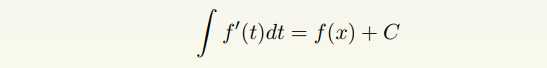
牛顿-莱布尼茨公式展示了微分与积分的基本关系: 在一定程度上微分与积分互 为逆运算.

 4、案例

求函数 ln(x) 的不定积分。

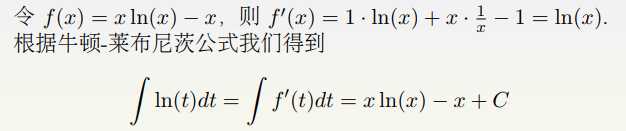
5、多变量函数的积分

如果积分区域形状不规则，可以用一个矩形把积分区域包起 来，并令函数在积分区域外边等于 0.

二重积分的几何意义是积分函数与 X − Y 坐标平面之间部 分的有向体积.

 6、积分学总结

积分的代数意义是无穷求和，几何意义是带符号的体积

微分和积分在一定程度上互为逆运算

熟悉微分公式有助于计算积分

多重积分可以理解成是依次进行的单重积分

四、随机变量与概率

1、离散随机变量（发生事件的几种情况，比如扔塞子。1-6为随机变量）

比如上述事件<=3就是1.2.3事件概率取值。

2、连续随机变量

对于每一个具体的取值的概率为0.

对于连续型随机变量，概率为概率密度函数的积分.

不论是离散还是连续型随机变量, 概率函数和概率密度函数 的定义域即为这个随机变量的值域.

作为一个特殊的概率函数，分布函数定义为 Φ(x) = P(X < x).

我们在此只考虑几乎处处连续的概率密度函数，我们不考虑离散，连续混 合型的随机变量

 3、概率

事件的概率（事件是一个集合）

整个概率空间是一个事件，这个事件一定发生所以全空间的 概率为 1

事件是随机变量值域的子集 S

事件的概率则表示 S 里面概率之和或概率密度之积分.

事件的条件概率

条件本身也是事件，也可表示为随机变量值域的子集:A

条件概率里面的事件，又是这个条件的子集:S ∩ A ⊂ A

概率其实就是集合的大小比例，而概率函数或者概率密度函数可以理解为比较 大小时候的权重

 4、贝叶斯公式

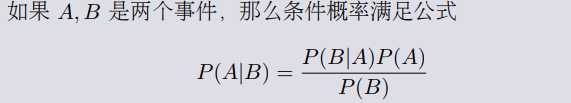
利用前面的定义我们知道，事件 A, B 同时发生的概率为 P(A ∩ B),

一方面 P(A ∩ B) = P(B|A)P(A)

另一方面对称的有 P(A ∩ B) = P(A|B)P(B)

所以 P(B|A)P(A) = P(A|B)P(B),

两边同时除以 P(B) 就得到 了贝叶斯公式.