斜率优化dp
本来想直接肝这玩意的结果还是被忽悠着做了两道数论
现在整天浑浑噩噩无心学习甚至都不是太想颓废是不是药丸的表现
各位要知道我就是故意要打删除线并不是因为排版错乱
反正就是一个del标签嘛并不是什么大事的说
讲道理这一篇要不是写laTex我就直接用html写了
Emmmm划掉的原因是因为跟正题一点关系都没有啊
不让自己写摘要我写第一段凑摘要好咯
第一次写花花绿绿的blog感觉还是很新鲜的
你看看我到了正文部分还划不划啊(该划的还是划╭(╯^╰)╮)
其实文章里有彩蛋比如这里 被你发现了OvO 哈哈
据说找到了所有的彩蛋能获得一些奖励(但很不幸这是假的
不过laTex公式也可以带颜色这真的是太棒啦
这一段对的如此不整齐的原因可能是为了逼死强迫症
明明是懒得把字数扣成一样的非要找这么个冠冕堂皇的借口么
上次我们说过
\[
f[i]=max\{f[j]+x[j]\}(j\in[1,i))
\]
这样的方程的优化(变量记录)和
\[
f[i]=max\{f[j]+x[j]\} (j\in[i-m,i))
\]
这样的方程的优化(单调队列), 但是如果遇到
\[
f[i]=max\{f[j]+g(i,j)\} (j\in[1,i)
\]
这样的方程, 就不会处理了... 这也就是今天要讲的斜率优化dp.
对于这种方程, 我们考虑将这个式子化成\(y\)=\(k\)\(x\)+\(b\)的形式, 其中\(y\)和\(x\)是只和\(j\)相关的式子, \(k\)是和\(i\)相关的式子, \(b\)是\(f[i]\)和其他什么常数, 然后根据类似于线性规划的知识维护一定的单调性来优化转移.
光这么讲也没什么意思嘛(鬼能看懂咯), 我们看例题. 其实就是bzoj1010 第一页就有 传送门在这里~
状态转移方程比较显然: 令\(f[i]\)表示装前\(i\)个东西的最小花费, \(sum[i]\)表示\(C_i\)的前缀和, 则
\[
f[i]=min\{f[j]+(sum[i]-sum[j]+i-j-1-L)^2\}
\]
这样我们已经可以\(O(n^2)\)做了, 不过并没有给部分分, 不知道能得几分, 反正\(n\leq5W\)想A掉是不可能的.这辈子都是不可能的. dp优化以后跑得又快, 又可以装逼, 我超喜欢优化的!
所以很明显需要优化. 那么就是说要化式子.我讨厌化式子!!!
为了方便, 我们令\(s[i]=sum[i]+i,C=L+1\), 那么
\[f[i]=f[j]+(s[i]-s[j]-C)^2=f[j]+(s[i]-C)^2-2(s[i]-C)*s[j]+s[j]^2\]
然后移项, 得到
\(f[j]+s[j]^2\)=\(2(s[i]-C)\)*\(s[j]\)+\(f[i]-(s[i]-C)^2\)
这样就出现了\(y\)=\(k\)\(x+\)\(b\)的形式. 根据线性规划一类的知识, 我们要在可行域中最小化\(f[i]\), 就是要最小化\(截距b\). 话说化带颜色的式子的时候的laTex也是挺好看的..
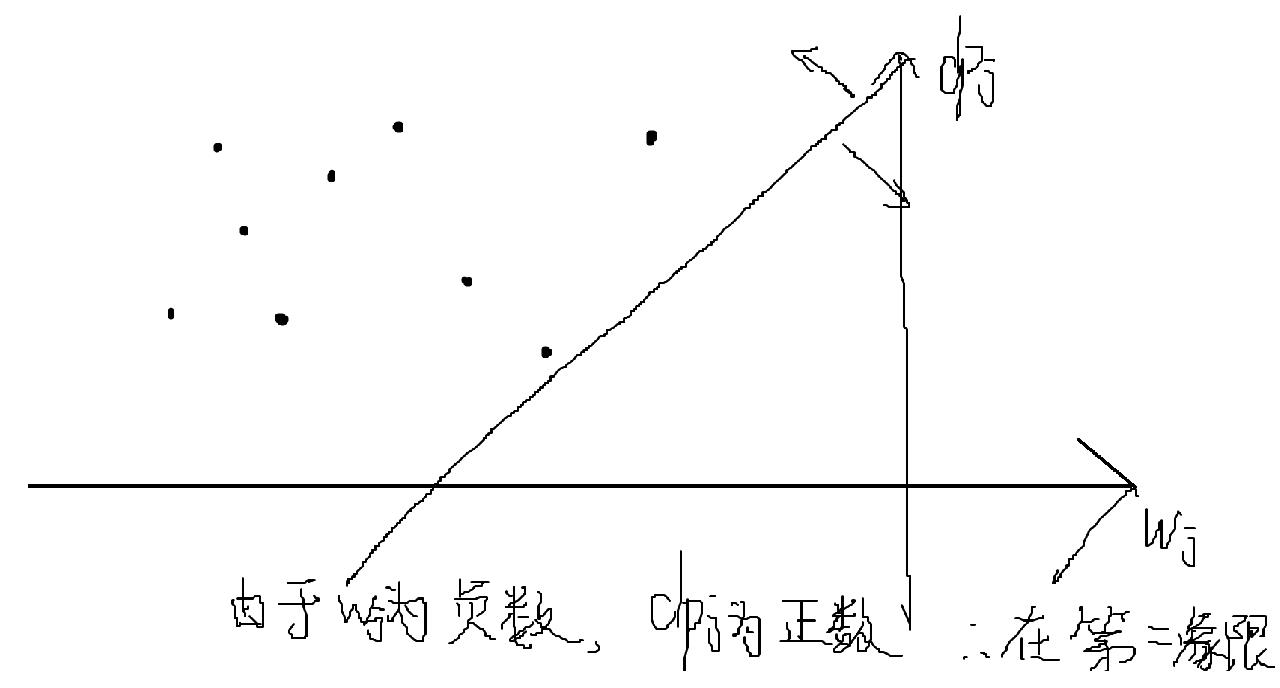
那么怎么最小化截距呢? 我们画个图. 画的很丑大家轻喷...
首先很明显我们dp的时候求好\(t\)的状态可以存在一个点\((x,\)\(y\)\()\)里面, 即\((s[t],\)\(f[t]-s[t]^2\)\()\). 这样我们每次就拿一条斜率为\(2(s[i]-C)\)的直线去里面找截距的最小值就行了. 但这样还是\(O(n^2)\)的, 因为我们没有充分利用单调性来去掉那些根本不可能优的点.

我们可以看到 如果将要插入的点是红色的, 那么无论斜率怎样, 它都不会比已经加入过的点优(截距更小), 我们就不需要考虑红色点了, 但是蓝色的点则是可能更优的, 那么我们就要保留蓝色点.
其实这里要证明决策单调性什么的 但画图就显得很直观 显然成立我们就不证了(明明是因为懒←_←
经过若干个点的验证, 我们发现, 可能更优的点都集中在下凸壳上!
那么我们维护下凸壳就好了. 这样的话转移的复杂度似乎从\(O(n)\)降到了\(O(H)\), 但似乎还是该怎么过不去就怎么过不去.
所以继续考虑, 为什么转移的时候非要遍历所有点呢?
我们惊奇地发现, 这个题有一个性质, 就是斜率\(k=2(s[i]-C)\)是递增的, 所以吧,
我们枚举下一个斜率的时候, 可以发现, 如果这个点与下一个点的连线的斜率比枚举的斜率小(前两个点), 那么截距就会比下一个点大, 而且由于斜率递增, 所以差距会越来越大, 那这个点我们就可以不要了. 所以我们就可以看出可以用一个单调队列来维护这个凸壳, 每次先把队首不合法的弹出, 然后取队首转移即可. 其实这里关于斜率的讨论应该是要化一波覆盖的式子的, 但是也是由图显然, 而且做半平面交的时候化过, 这里就不化了(显然还是因为懒←_←
这样的话转移的时间复杂度就从\(O(H)\)降到了\(O(1)\), 总复杂度也就降到了\(O(n)\)的水平, 就可以非常愉快的通过此题啦~ 所以不是很懂一个正解\(O(n)\)的题目给个\(n\leq5W\)的数据范围是几个意思...
惊奇地发现自己调了一个晚上的原因竟然是化式子移项正负号反了??? 应该打回小学重造.
本来想用叉积结果化出来的式子太臃肿 我当时还不知道自己式子化错了然后不好调就删掉改成斜率了.
非常不喜欢这样损精度的方式但其实都是整数所以还好, 但是后来发现式子化错了之后懒得改就这么写下去了...
有一点就是5W*1e7要开long long.. 其实代码非常简单... 就这么几行你还调了一晚上←_←
#include <cmath>
#include <cstdio>
const int N=5e4+5;
typedef long long LL;
inline int gn(int a=0,char c=0){
for(;c<'0'||c>'9';c=getchar());
for(;c>47&&c<58;c=getchar())a=a*10+c-48;return a;
}
LL s[N],f[N];int q[N],h=0,t=0,n,l;
double slope(int x,int y){return 1.0*(f[x]+s[x]*s[x]-f[y]-s[y]*s[y])/(s[x]-s[y]);}
int main(){
n=gn(),l=gn()+1;
for(int i=1;i<=n;++i) s[i]=s[i-1]+gn()+1;
for(int i=1;i<=n;++i){
while(h<t&&slope(q[h],q[h+1])<=2*(s[i]-l)) ++h;
f[i]=f[q[h]]+(s[i]-s[q[h]]-l)*(s[i]-s[q[h]]-l);
while(h<t&&slope(q[t],q[t-1])>=slope(i,q[t])) --t;
q[++t]=i;
} printf("%lld",f[n]);
}我觉得代码写的非常清楚了 就这样吧...
怎么样,找到所有透明的字了嘛?? 哈哈哈~