triples(牛客多校) (贪心,位运算,构造体)

Posted 2023-04-17 小幻

题目大意: 

给定一个a，要求构造最少个数的3的倍数使得这些数的按位或和为a.

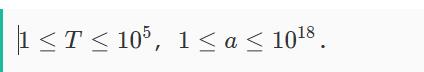
 思路 :

• 3的倍数, 就要利用3的性质

• 

• 所以在绝大数的情况下, 只需要2个数即可

• 考虑如何构造, 他给的是 | , 就牢牢利用|的性质, 2个数可以有重复位上的 1, 就先让2个数都等于 a ,然后在去删除对应多的位数

• 然后对于 a%3=1和 a%3=2 分类讨论 ,在

 

2022牛客多校2补题

2022牛客多校2补题

更好观感

G Link with Monotonic Subsequence

$max(lis(p),lds(p))$ 的下界为 $\lceil \sqrt{n}\rceil$

如果 $n=k^2$ 构造出 $(n-k+1,n-k+2,...,n)(k+1,...,2\times k)(1,2,3,...,k)$

规律也可以通过打表得到

打表程序主体

for(int i = 6; i <= 6; i++)

    vi a(i);
    iota(a.begin(), a.end(), 1);
    int ans = 1e9;
    vi t;
    do
    
        vi dpd(i, 1), dpi(i, 1);
        for(int j = 0; j < i; j++)
            for(int k = 0; k < j; k++)
                if(a[j] < a[k])
                    dpd[j] = max(dpd[j], dpd[k] + 1);

        for(int j = 0; j < i; j++)
            for(int k = 0; k < j; k++)
                if(a[j] > a[k])
                    dpi[j] = max(dpi[j], dpi[k] + 1);
        int in = 0, de = 0;
        for(int j = 0; j < i; j++)
        
            in = max(in, dpi[j]);
            de = max(de, dpd[j]);
        
        if(max(in, de) < ans)
        
            ans = max(in, de);
            t = a;
        
    while(next_permutation(a.begin(), a.end()));
    for(auto x : t)
        cout << x << " ";
    cout << "\\n";

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;

void solve()

	int n;
	cin >> n;
	int len = sqrt(n);
	if(len * len != n) len ++;

	int val = 0;

	if(n % len)
	
		val += n % len;
		for(int i = 1; i <= n % len; i++)
			cout << val-- << " ";
		val += n % len + len;
	
	else val += len;

	for(int i = 1; i <= n / len; i++)
	
		for(int j = 1; j <= len; j++)
			cout << val-- << " ";
		val += len * 2;
	
	cout << "\\n";


int main()

	ios::sync_with_stdio(false);
	cin.tie(0);

	int t;
	t = 1;
	cin >> t;
	while(t--)
		solve();
	return 0;

D Link with Game Glitch

n种物品，m种交换，每 $a_i$ 个 $b_i$ 类物品可以换 $w\cdot c_i$ 个 $d_i$ 类物品。求最大的 w 使不存在一种无限交换的方式。

从 $b_i$ 向 $d_i$ 连一条 $w\cdot c_i/a_i$ 的边。

二分 $w$ ，如果图中出现边乘积大于 1 的环，即存在无限转换的方式，否则不存在。

因为边乘积较大，需要转换为 $log$ 进行处理。
$$log(w_1\cdot w_2\cdot ...\cdot w_n)=log{w}_1+log{w}_2+...+log{w}_n$$
边权乘积转化为边权log和。

即为存在边权和大于等于0的环即是无限转换，我们把边权取符号，即存在小于等于0的环即为无线转换。所以转换为判断是否存在负环。

判断负环使用SPFA，建立一个超级源点，使其可以到达所有点。

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using db = double;
using ld = long double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using tu = tuple<int, int, db>;
using vi = vector<int>;
using vl = vector<ll>;
const int dx[] = -1, 0, 1, 0, dy[] = 0, 1, 0, -1;
const int N = 1e3 + 5, M = 3 * N;
const int mod = 1e9 + 7;
const ld eps = 1e-8;

int n, m;
int e[M], h[N], ne[M], idx;
db w[M], dis[N];

void add(int a, int b, db c)

	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;

void solve()

	cin >> n >> m;

	memset(h, -1, sizeof h);
	for(int i = 1; i <= n; i++)
		add(0, i, 0);
	for(int i = 1; i <= m; i++)
	
		int a, b, c, d;
		cin >> a >> b >> c >> d;
		add(b, d, log(a) - log(c));
	

	auto check = [&](db x) -> bool
	
		for(int i = 1; i <= n; i++)
			dis[i] = 1e9;
		vector<db> W(idx);
		for(int i = 0; i < idx; i++)
		
			if(i < n) W[i] = w[i];
			else W[i] = w[i] - log(x);
		

		vector<bool> vis(n + 1);
		vi cnt(n + 1);
		queue<int> q;
		q.push(0);
		dis[0] = 0;
		vis[0] = true;
		while(!q.empty())
		
			int u = q.front();
			q.pop();
			vis[u] = false;

			for(int i = h[u]; ~i; i = ne[i])
			
				int v = e[i];
				db ww = W[i];
				if(dis[u] + ww < dis[v])
				
					dis[v] = dis[u] + ww;
					cnt[v]++;
					if(cnt[v] >= n) return false;
					if(!vis[v])
					
						vis[v] = true;
						q.push(v);
					

				
			
		
		return true;
	;

	db l = 0, r = 1;
	while(r - l > eps)
	
		db mid = (l + r) / 2;
		if(check(mid)) l = mid;
		else r = mid;
	
	cout << fixed << setprecision(10) << l << "\\n";

int main()

	ios::sync_with_stdio(false)以上是关于triples(牛客多校) (贪心,位运算,构造体)的主要内容，如果未能解决你的问题，请参考以下文章
 
 2021牛客多校10 - Train Wreck(贪心)
 2022牛客多校2补题
 2022牛客多校2补题
 2022牛客多校2补题
 2022牛客多校2补题
 2021牛客多校3 - 24dian(dfs)