考研数据结构模板:顺序表链表栈队列
Posted 珂霖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了考研数据结构模板:顺序表链表栈队列相关的知识,希望对你有一定的参考价值。
考研数据结构模板:顺序表、链表、栈、队列
考研数据结构模板:顺序表、链表、栈、队列
前言
- 代码风格偏向于考研风格而非算法竞赛风格。
- 代码实现参考《2024数据结构王道复习指导》。
- 注释详细、保证看懂。
- 下面是已实现的数据结构模板:
- 顺序表SeqList
- 链表LinkList
- 双链表DLinkList
- 顺序栈SeqStack
- 循环顺序队列CircleQueue
- 链队列LinkQueue
顺序表SeqList
顺序表定义
// 定义顺序表
struct SeqList
int *data; // 数据动态分配
int length, maxLength; // 当前长度、最大长度
;
// 最大容量
#define SEQ_LIST_MAX_SIZE 100
// 初始容量
#define SQL_LIST_INIT_SIZE 10
初始化
void SeqListInitial(SeqList &list)
list.maxLength = SQL_LIST_INIT_SIZE;
list.data = new int[list.maxLength];
list.length = 0;
判断是否为空
bool SeqListIsEmpty(SeqList &list)
return list.length == 0;
查询元素长度
int SeqListLength(SeqList &list)
return list.length;
打印元素
void SeqListPrint(SeqList &list)
for (int i = 0; i < list.length; i++)
printf("%d ", list.data[i]);
插入元素
bool SeqListInsert(SeqList &list, int index, int data)
if (index < 1 || index > list.length + 1) // index范围必须在[1, list.SeqListLength + 1]
return false; // 下标溢出
if (list.length == list.maxLength) // 空间不足,申请空间
if (list.length == SEQ_LIST_MAX_SIZE)
return false; // 空间溢出
else
int maxLength; // 下一次申请空间的长度
if (list.length * 2 < SEQ_LIST_MAX_SIZE)
maxLength = list.length * 2; // 容量每次扩大两倍
else
maxLength = SEQ_LIST_MAX_SIZE;
int *memory = new int[maxLength]; // 创建一块存储空间
for (int i = 0; i < list.length; i++) // 复制数组
memory[i] = list.data[i];
delete list.data; // 释放原来的空间
list.data = memory;
list.maxLength = maxLength;
for (int i = list.length; i >= index; i--) // 移动数组
list.data[i] = list.data[i - 1];
list.length++;
list.data[index - 1] = data; // 插入元素
return true;
删除元素
bool SeqListRemove(SeqList &list, int index, int &data)
if (index < 1 || index > list.length) // index取值范围为[1, list.SeqListLength]
return false; // 溢出
data = list.data[index - 1]; // 保存删除的数据
for (int i = index; i < list.length; i++) // 移动元素
list.data[i - 1] = list.data[i];
list.length--;
return true;
查询元素位置
int SeqListFindIndex(SeqList &list, int data)
for (int i = 0; i < list.length; i++) // 遍历数组
if (list.data[i] == data)
return i + 1;
return -1; // 找不到则返回-1
查询位置上的元素值
bool SeqListGet(SeqList &list, int index, int &data)
if (index < 1 || index > list.length) // 下标范围在[1, list.length]之间
return false;
data = list.data[index - 1]; // 保存元素
return true;
链表LinkList
链表定义
// 单链表节点
struct LinkListNode
int data;
LinkListNode *next;
;
// 单链表
struct LinkList
LinkListNode *head; // 头指针
LinkListNode *tail; // 尾指针
;
空元素初始化
void LinkListInitial(LinkList &list)
LinkListNode *node = new LinkListNode(); // 初始化头节点
list.head = node;
list.tail = node;
数组初始化
void LinkListInitial(LinkList &list, int data[], int length)
LinkListNode *node = new LinkListNode();
list.head = node;
list.tail = node;
for (int i = 0; i < length; i++) // 尾插法插入所有元素
LinkListNode *next = new LinkListNode();
next->data = data[i];
list.tail->next = next;
list.tail = list.tail->next;
查询元素长度
int LinkListLength(LinkList &list)
int length = 0;
LinkListNode *p = list.head->next;
while (p != NULL) // 遍历链表直到为空
length++;
p = p->next;
return length;
打印元素
void LinkListPrint(LinkList &list)
if (list.head == list.tail)
return;
LinkListNode *p = list.head->next;
while (p != NULL) // 遍历所有元素,直到为空
printf("%d ", p->data);
p = p->next;
插入元素
bool LinkListInsert(LinkList &list, int index, int data)
if (index < 1) // 下标范围必须大于等于1
return false;
LinkListNode *p = list.head; // 用于保存插入位置的前驱
for (int i = 1; i < index; i++) // 找到插入位置的前驱
p = p->next;
if (p == NULL)
return false; // 不存在此下标
LinkListNode *node = new LinkListNode(); // 插入元素
node->data = data;
node->next = p->next;
p->next = node;
return true;
删除元素
bool LinkListRemove(LinkList &list, int index, int &data)
if (index < 1) // 下标范围必须大于等于1
return false;
LinkListNode *p = list.head; // 用于保存插入位置的前驱
for (int i = 1; i < index; i++) // 查找删除位置的前驱
p = p->next;
if (p == NULL)
return false; // 不存在此下标
LinkListNode *node = p->next; // 执行删除操作
data = node->data; // 保存删除节点的值
p->next = node->next;
delete node; // 释放空间
return true;
查询位置上的元素值
bool LinkListGet(LinkList &list, int index, int &data)
if (index < 1) // 下标范围必须大于等于1
return false;
LinkListNode *p = list.head;
for (int i = 1; i <= index; i++) // 遍历链表
p = p->next;
if (p == NULL)
return false; // 不存在此下标
data = p->data;
return true;
双链表DLinkList
双链表定义
// 双链表节点
struct DLinkListNode
int data;
DLinkListNode *prev, *next; // 前驱与后继节点
;
// 双链表
struct DLinkList
DLinkListNode *head; // 头节点
;
初始化
void DLinkListInitial(DLinkList &list)
DLinkListNode *head = new DLinkListNode(); // 创建头节点
list.head = head;
打印元素
void DLinkListPrint(DLinkList &list)
DLinkListNode *p = list.head;
while (p->next != NULL)
p = p->next;
printf("%d ", p->data);
插入元素
bool DLinkListNodeInsert(DLinkList &list, int index, int data)
if (index < 1) // 下标范围必须大于等于1
return false;
DLinkListNode *p = list.head;
for (int i = 1; i < index; i++) // 找到插入位置的前驱
p = p->next;
if (p == NULL)
return false; // 不存在此下标
DLinkListNode *node = new DLinkListNode(); // 插入元素
node->data = data;
node->next = p->next;
if (p->next != NULL)
p->next->prev = node;
node->prev = p;
p->next = node;
return true;
删除元素
bool DLinkListRemove(DLinkList &list, int index)
if (index < 1) // 下标范围必须大于等于1
return false;
DLinkListNode *p = list.head; // 找到删除位置的前驱
for (int i = 1; i < index; i++)
p = p->next;
if (p == NULL)
return false; // 不存在此下标
DLinkListNode *q = p->next; // 被删除的元素
if (q == NULL) // 当q为链表末尾时,则被删除的元素不存在
return false;
p->next = q->next;
if (q->next != NULL)
q->next->prev = p;
delete q; // 释放空间
return true;
顺序栈SeqStack
顺序栈定义
// 最大空间
#define SEQ_STACK_MAX_SIZE 100
// 顺序栈
struct SeqStack
int data[SEQ_STACK_MAX_SIZE];
int top; // 栈顶指针
;
初始化
void SeqStackInitStack(SeqStack &stack)
stack.top = -1; // 使用-1标识为空栈
判断是否为空
bool SeqStackIsEmpty(SeqStack &stack)
return stack.top == -1;
进栈
bool SeqStackPush(SeqStack &stack, int data)
if (stack.top == SEQ_STACK_MAX_SIZE - 1)
return false; // 空间不够
stack.data[++stack.top] = data; // 指针后移并添加元素
return true;
出栈
bool SeqStackPop(SeqStack &stack, int &data)
if (stack.top == -1)
return false; // 没有元素
data = stack.data[stack.top--]; // 删除元素并将指针前移
return true;
读取栈顶元素
bool SeqStackGetTop(SeqStack &stack, int &data)
if (stack.top == -1)
return false; // 没有元素
data = stack.data[stack.top];
return true;
循环顺序队列CircleQueue
循环顺序队列定义
// 最大空间
#define CIRCLE_QUEUE_MAX_SIZE 10
// 循环顺序队列
struct CircleQueue
int data[CIRCLE_QUEUE_MAX_SIZE];
int front, rear; // 头指针和尾指针
;
初始化
void CircleQueueInit(CircleQueue &queue)
queue.front = queue.rear = 0;
判断队列是否为空
bool CircleQueueIsEmpty(CircleQueue &queue)
return queue.front == queue.rear;
判断队列是否已满
bool CircleQueueIsFull(CircleQueue &queue)
return (queue.rear + 1) % CIRCLE_QUEUE_MAX_SIZE == queue.front; // 队尾的下一个位置是队头,则说明队满
获取队列长度
int CircleQueueLength(CircleQueue &queue)
return (queue.rear - queue.front + CIRCLE_QUEUE_MAX_SIZE) % CIRCLE_QUEUE_MAX_SIZE;
进队
bool CircleQueuePush(CircleQueue &queue, int data)
if (CircleQueueIsFull(queue)) // 如果队列已满,则无法进队
return false;
queue.data[(queue.rear++) % CIRCLE_QUEUE_MAX_SIZE] = data; // 取模实现循环
return true;
出队
bool CircleQueuePop(CircleQueue &queue, int &data)
if (CircleQueueIsEmpty(queue)) // 如果队列为空,则无法出队
return false;
data = queue.data[(queue.front++) % CIRCLE_QUEUE_MAX_SIZE];
return true;
链队列LinkQueue
链队列定义
// 链队列节点
struct LinkQueueNode
int data;
LinkQueueNode *next;
;
// 链队列
struct LinkQueue
LinkQueueNode *front, *rear; // 头指针和尾指针
;
初始化
void LinkQueueInit(LinkQueue &queue)
LinkQueueNode *head = new LinkQueueNode(); // 头节点
queue.front = queue.rear = head;
判断队列是否为空
bool LinkQueueIsEmpty(LinkQueue &queue)
return queue.front == queue.rear;
获取队列长度
int LinkQueueLength(LinkQueue &queue)
int length = 0;
// 遍历链表直到为空
LinkQueueNode *p = queue.front->next;
while (p != NULL)
length++;
p = p->next;
return length;
进队
void LinkQueuePush(LinkQueue &queue, int data)
LinkQueueNode *node = new LinkQueueNode(); // 头节点
node->data = data;
queue.rear->next = node;
queue.rear = queue.rear->next;
出队
bool LinkQueuePop(LinkQueue &queue, int &data)
if (LinkQueueIsEmpty(queue))
return false; // 队列为空
LinkQueueNode *head = queue.front; // 头节点
LinkQueueNode *node = head->next;
data = node->data;
queue.front = node; // 新的头节点
delete head; // 释放空间
return true;
顺序表栈与队列
一、顺序表引入
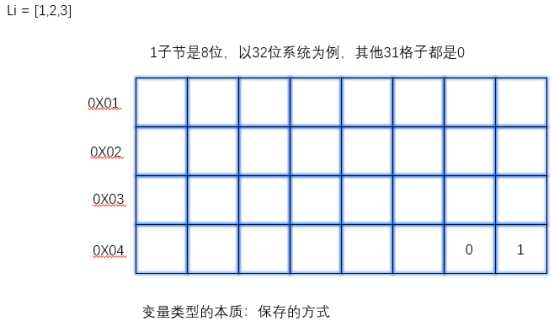
1什么是线性表
1 在程序中,经常需要将一组数据元素作为整体管理和使用,需要创建这种元素组,用变量记录它们,传进传出函数等。 2 一组数据中包含的元素个数可能发生变化(增加或删除元素)。 3 对于这种需求,最简单的解决方案便是将这样一组元素看成一个序列,用元素在序列里的位置和顺序,表示实际应用中 的某种有意义的信息,或者表示数据之间的某种关系。 4 这样的一组序列元素的组织形式,我们可以将其抽象为线性表。 5 一个线性表是某类元素的一个集合,还记录着元素之间的一种顺序关系。 6 线性表是最基本的数据结构之一,在实际程序中应用非常广泛,它还经常被用作更复杂的数据结构的实现基础。
2 什么是顺序表
1 根据线性表的实际存储方式,分为两种实现模型: 2 顺序表,将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示。 3 链表,将元素存放在通过链接构造起来的一系列存储块中。
二、顺序表的基本形式
基本存储形式
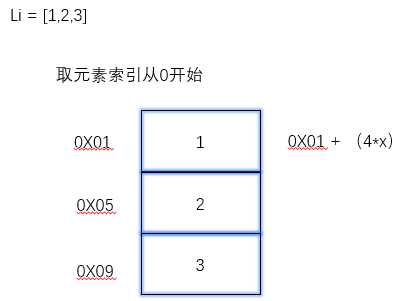
元素外置的顺序表
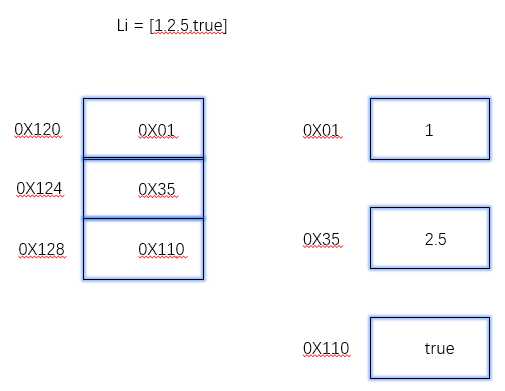
三 顺序表的结构与实现
1 顺序表的结构
1 一个顺序表的完整信息包括两部分 2 一部分是表中的元素集合 3 另一部分是为实现正确操作而需记录的信息,即有关表的整体情况的信息,这部分信息主要包括元素存储区的容量和当前表中已有的元素个数两项。

2 顺序表的两种基本实现方式
l 一体式存储,类似于数组,不可变长度
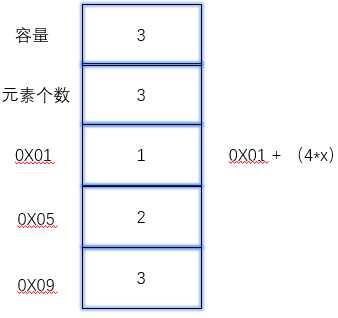
l 分离式存储,类似于列表,可变长度
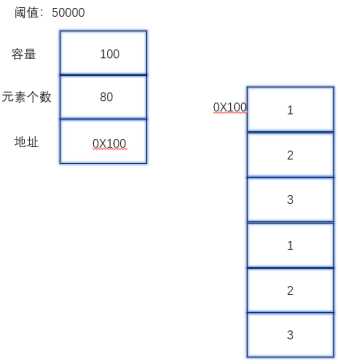
3 扩容的两种策略
1 每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。
2 每次扩充容量加倍,如每次扩充增加一倍存储空间。
四、顺序表的操作
1 插入元素
l 为顺序表插入新元素111的三种方式时间复杂度为多少?
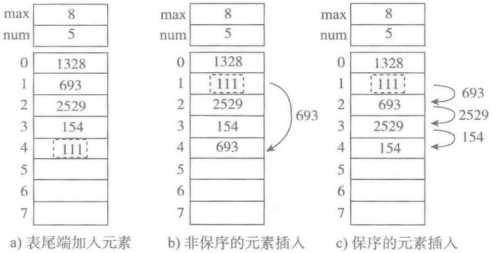
a:O(1)
b:O(1)
c:O(n)
2 删除元素
l 删除顺序表中元素的三种方式时间复杂度为多少?
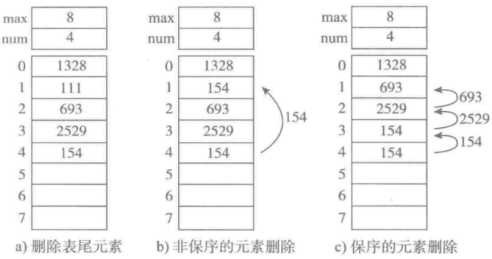
a:O(1)
b:O(1)
c:O(n)
五:Python中的顺序表
1 Python中的list和tuple两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的性质
2 tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性质类似
1. list的基本实现技术
1 Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的顺序(即保序),而且还具有以下行为特征: 1)基于下标(位置)的高效元素访问和更新,时间复杂度应该是O(1),为满足该特征,应该采用顺序表技术, 表中元素保存在一块连续的存储区中。 2)允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变,为满足该特征, 就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分离式实现技术。 2 在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x)或list.insert(len(list), x),
即尾部插入,比在指定位置插入元素效率高。 3 在Python的官方实现中,list实现采用了如下的策略: 1)在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区。 2)在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。 3)但如果此时的表已经很大(目前的阈值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式, 是为了避免出现过多空闲的存储位置。
六 栈
1 栈的概念:
1 栈(stack)是一种容器,可存入数据元素、访问元素、删除元素。 2 它的特点在于只能允许在容器的一端(称为栈顶端指标)进行加入数据(push)和输出数据(pop)的运算。 3 没有了位置概念,保证任何时候可以访问、删除的元素都是此前最后存入的那个元素,确定了一种默认的访问顺序。 4 由于栈数据结构只允许在一端进行操作,因而按照后进先出(Last In First Out)的原理运作,简称LIFO。
2 栈(ADT)的操作
1 Stack() 创建一个新的空栈 2 push(item) 添加一个新的元素item到栈顶 3 pop() 弹出栈顶元素 4 peek() 返回栈顶元素 5 is_empty() 判断栈是否为空 6 size() 返回栈的元素个数
3 栈的代码实现
class Stack: # 初始化空栈 def __init__(self): self.__list = [] def push(self, item): self.__list.append(item) def pop(self): if self.__list: return self.__list.pop() else: return None def peek(self): if self.__list: return self.__list[-1] else: return None def is_empty(self): return self.__list is None def size(self): return len(self.__list) if __name__ == ‘__main__‘: s = Stack() s.push(1) s.push(2) s.push(3) print(s.pop()) print(s.pop()) print(s.pop())
七:队列
1 什么是队列
1 队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
2 队列是一种先进先出的(First In First Out)的线性表,简称FIFO。
2 队列的操作
1 Queue() 创建一个新的空队列 2 enqueue(item) 往队列中添加一个item元素 3 dequeue() 从队列头部删除一个元素 4 is_empty() 判断一个队列是否为空 5 size() 返回队列的大小
3 队列功能的实现
# 定义队列 class Queue: # 初始化 def __init__(self): self.__list = [] def enqueue(self,item): self.__list.append(item) def dequeue(self): return self.__list.pop(0) def is_empty(self): return self.__list is None def size(self): return len(self.__list) if __name__ == ‘__main__‘: q = Queue() q.enqueue(1) q.enqueue(2) q.enqueue(3) print(q.dequeue()) print(q.dequeue()) print(q.dequeue())
八、双端队列
1 什么是双端队列
1 双端队列(deque,全名double-ended queue),是一种具有队列和栈的性质的数据结构。
2 双端队列中的元素可以从两端弹出,其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。
2 双端队列的操作
1 Deque() 创建一个空的双端队列 2 add_front(item) 从队头加入一个item元素 3 add_rear(item) 从队尾加入一个item元素 4 pop_front() 从队头取一个item元素 5 pop_rear() 从队尾取一个item元素 6 is_empty() 判断双端队列是否为空 7 size() 返回队列的大小
3 双端队列的代码实现
class Deque: def __init__(self): self.__list = [] def add_front(self,item): self.__list.insert(0,item) def add_rear(self,item): self.__list.append(item) def pop_front(self): return self.__list.pop(0) def pop_rear(self): return self.__list.pop() def is_empty(self): return self.__list is None def size(self): return len(self.__list) if __name__ == ‘__main__‘: d = Deque() d.add_front(1) d.add_front(2) d.add_rear(3) d.add_rear(4) print(d.size()) print(d.pop_front()) print(d.pop_front()) print(d.pop_rear()) print(d.pop_rear())
以上是关于考研数据结构模板:顺序表链表栈队列的主要内容,如果未能解决你的问题,请参考以下文章