范数经典问题的推导与分析
Posted 信
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了范数经典问题的推导与分析相关的知识,希望对你有一定的参考价值。
本文将主要围绕范数的经典问题进行推导、分析。
LASSO问题
推导
问题定义:\\(\\undersetx\\min||y-X\\beta||_2^2+\\tau||\\beta||_\\mathcalA\\)
问题推导:
0、上述问题是典型的无约束问题,可以通过变量替换的思想进行处理。
1、令\\(z=X\\beta\\),上述问题更新为\\(g(u)=\\min_\\beta,z=\\frac12\\Vert y-z\\Vert_2^2+\\lambda\\Vert\\beta\\Vert_1+u^T(z-X\\beta)\\).
2、可以观察到\\(g(u)\\)中关于\\(\\beta\\)和\\(z\\)的元素项不存在耦合关系,因此可进步将\\(g(u)\\)问题拆解为独立的最小项\\(g(\\beta)\\)和\\(g(z)\\),其中\\(g(\\beta)=\\min_\\beta~\\lambda\\Vert\\beta\\Vert_1-u^TX\\beta\\), \\(g(z)=\\min_\\beta~\\frac12 \\Vert y-z\\Vert_2^2+u^Tz\\)
3、\\(g(\\beta)=\\min_\\beta~\\lambda\\Vert\\beta\\Vert_1-u^TX\\beta=-\\max_\\beta~\\lambda(-\\Vert\\beta\\Vert_1+\\fracu^TX\\beta\\lambda)=-\\lambda~g^*(\\fracX^Tu\\lambda)=-\\lambda I_\\v_i|\\Vert v\\Vert_\\infty \\leq1\\(\\fracX^Tu\\lambda)\\),这个最小项可以表征为示性函数形式,示性函数\\(f^*(y)=\\begincases0&||y||_*\\leq1\\\\ \\infty&\\textotherwise\\endcases=I_\\z:||z||_*\\leq1\\(y)\\).
4、对\\(g(z)\\)求极值,可以得到\\(-(y-z)+u=0\\),即\\(z=y-u\\).
5、将上述约束代入\\(g(z)\\),可以得到下式:
\\(g(z)=\\frac12\\Vert u\\Vert^2_2+u^T(y-u)=u^Ty-\\frac12\\Vert u\\Vert_2^2=-\\frac12[\\Vert y\\Vert_2^2+\\Vert u\\Vert_2^2-2u^Ty]+\\frac12\\Vert y\\Vert_2^2=-\\frac12\\Vert y-u\\Vert_2^2+\\frac12 \\Vert y\\Vert_2^2\\)
那么对偶问题可以表示为如下形式:
\\(\\max_u -\\frac12\\Vert y-u\\Vert_2^2+\\frac12 \\Vert y\\Vert_2^2 ~s.t.X^Tu\\leq\\lambda\\)
代码
原子范数对偶问题
推导
有噪声情况下,原子范数的原问题可以抽象为:\\(\\operatorname*min_x\\|x\\|_\\mathcalA\\mathrmsubject~to\\left\\\\beginarrayl\\mathbfy=\\mathcalF_Mx+\\mathbfn,\\\\ \\|\\mathbfn\\|_2\\leq\\epsilon.\\endarray\\right.\\)
对偶函数可以写为\\(g(x,u)\\)在\\(C\\)上的下确界,即\\(g(\\mathbfc,\\xi)=\\inf~L(x,\\mathbfc,\\xi)\\)
下面对原问题的对偶问题进行推导:
1、原问题的增广拉格朗日目标函数可以表示为:\\(L(x,\\mathbfc,\\xi)=\\|x\\|_\\mathcalA+\\mathrmRe\\left[\\mathbfc^H\\left(\\mathbfy-\\mathcalF_Mx-\\mathbfn\\right)\\right]+\\xi\\left(\\mathbfn^H\\mathbfn-\\epsilon^2\\right)\\)
将拉格朗日方程进行重写,\\(\\inf~L(x,\\mathbfc,\\xi)=\\mathrmRe[c^Hy-c^Hn]+\\xi[n^Hn-\\epsilon^2]+\\inf[\\Vert x\\Vert_A-\\mathrmRe[\\lambda^HF_Mx]]\\\\\\)
2、下确界的求解是关于\\(x\\)的最小化,因此对原拉格朗日增广函数的最小化可以转换为对\\([\\Vert x\\Vert_A-\\mathrmRe[\\lambda^HF_Mx]]\\)求下确界。在求这项下确界时,需要对式中的噪声功率参数\\(n\\)和对偶变量\\(\\xi\\)求偏导寻找极值点。
当对噪声功率参数\\(n\\)求偏导时[目的是为了使噪声功率最小化],有\\(\\frac\\partial g(\\mathbfc,\\xi)\\partial c=-c+2\\xi n=0\\),可以得到最佳极值点\\(n_o=\\fracc2\\xi\\),此时对应的对偶函数为\\(\\beginarraycg(\\mathbfc,\\xi)|_\\mathbfn_\\circ=\\mathrmRe\\left[\\mathbfc^H\\mathbfy\\right]-\\dfrac\\mathbfc^H\\mathbfc2\\xi+\\xi\\left(\\dfrac\\mathbfc^H\\mathbfc4\\xi^2-\\epsilon^2\\right)+\\+\\inf_x\\left(\\|x\\|_\\mathcalA-\\mathrmRe\\left[\\mathbfc^H\\mathcalF_Mx\\right]\\right).\\endarray\\)
当对对偶变量\\(\\xi\\)求偏导时,有\\(\\frac\\partial g(\\mathbfc,\\xi)_n_o\\partial \\xi=\\fracc^Hc4\\xi^2-\\epsilon^2=0\\),可以得到最佳极值点\\(\\xi_0=\\frac\\Vert c\\Vert2\\epsilon\\).
最后,基于最优极值点对偶函数可以表示为\\(g(c)|_n_o,\\xi_o=\\mathrmRe[c^Hy-\\epsilon\\Vert c\\Vert_2+\\inf_x(\\Vert x\\Vert_A-\\mathrmRe[c^H\\mathcalF_M]x)]\\).
对于下确界项,对每个\\(x_i\\),有\\(\\mathrmRe[(c^H\\mathcalF_M)_ix_i]=\\mathrmRe[(\\mathcalF_M^Hc)^H_ix_i]=|(\\mathcalF_M^Hc)_i||x_i|\\cos\\phi_i\\),\\(\\phi_i\\)表示\\(x_i\\)和\\(F_M^Hc\\)间的角度,基于此可以得到以下结论:\\(\\beginarrayc|x_i|-\\mathrmRe\\left[\\left(\\mathcalF_M^H\\mathbfc\\right)_i^Hx_i\\right]=|x_i|\\left[1-|\\left(\\mathcalF_M^H\\mathbfc\\right)_i|\\cos\\phi_i\\right]\\geq|x_i|\\left[1-|\\left(\\mathcalF_M^H\\mathbfc\\right)_i|\\right].\\endarray\\)
当\\(|\\mathcalF_M^Hc|\\leq1\\)时下确界项为0;当\\(|x_i|\\left[1-|\\left(\\mathcalF_M^H\\mathbfc\\right)_i|\\right]<0\\)时下确界可以达到\\(-\\infty\\)。
3、整理上述讨论,有噪声下的原子范数的对偶问题可以表征为:
\\(g(\\mathbfc)=\\left\\\\beginarraylcl\\operatornameRe\\left[\\mathbfc^H\\mathbfy-\\epsilon\\Vert c\\Vert_2\\right],&\\|\\mathcalF_M^H\\mathbfc\\|_\\infty\\leq1\\\\ -\\infty,&\\quad\\mathrmotherwise.\\endarray\\right.\\)
在上式中,\\(\\mathcalF_M^H\\mathbfc\\)中\\(\\mathcalF_M^H\\)表示逆FFT算子,对偶多项式可以表示为\\(H(z)=\\mathcalF_M^H\\mathbfc=\\sum\\limits_m=0^M-1c_m z^m=\\sum\\limits_m=0^M-1c_m e^-j\\left(2\\pi\\fracd\\lambdat\\right)m\\),其中\\(z(t)=e^-j\\left(2\\pi\\fracd\\lambdat\\right)\\).
4、为了进一步抽象\\(g(\\mathbfc)\\),我们可以作以下表示:
令\\(a(\\omega)=[1,e^j\\omega,...,e^j\\omega(L-1)]^T\\)为\\(L-1\\)次的三角多项式向量,那么因果三角多项式可以表征为:\\(H(\\omega)=\\sum_l=0^L-1h_l e^-j\\omega l=\\mathbfa(\\omega)^H\\mathbfh\\),其中\\(\\textbfh=\\left[h_0,\\cdots,h_L-1\\right]^T\\in\\mathbbC^L\\)表示多项式系数向量.
对于非负三角多项式,可以有Hermitian矩阵\\(R(\\omega)=|H(\\omega)|^2=H(\\omega)H(\\omega)^H=a(\\omega)^Hhh^Ha(\\omega)=\\sum_k=-(L-1)^L-1r_k e^-j\\omega k\\),其中\\(r_k=\\sum_l=0^L-1-kh_l h_l+k^*\\),\\(k\\geq0\\)并且\\(r_-k=r_k^*\\),稀疏\\(r_k\\)可以通过自相关矩阵\\(Q_L\\times L=hh^H\\)的第\\(k\\)条对角线元素进行计算\\(r_k=\\sum_i=1^L-kQ_i,i+k\\).
令两个多项式\\(H(\\omega)\\)和\\(B(\\omega)\\)满足以下不等关系:\\(|H(\\omega)|\\leq|B(\\omega)|,\\forall\\omega\\in[-\\pi,\\pi]\\)
这意味着\\(|H(\\omega)|^2\\leq|B(\\omega)|^2,\\forall\\omega\\in[-\\pi,\\pi]\\),定义\\(R_H(\\omega)=|H(\\omega)|^2\\)和\\(R_B(\\omega)=|B(\\omega)|^2\\),那么有\\(R_H(\\omega)\\leq R_B(\\omega)\\),即\\(Q_H \\leq Q_B\\),其中\\(Q_H=hh^H\\)和\\(Q_B=bb^H\\)为自相关向量\\(\\mathbfh=[h_0,\\cdots,h_L-1]^T\\)和\\(\\mathbfb=[b_0,\\cdots,b_L-1]^T\\)的自相关矩阵.
根据Schur补条件有\\(Q_B-hh^H\\geq0\\),即\\(\\beginbmatrix\\mathbfQ_B&\\mathbfh_L\\times1\\\\ \\mathbfh_1\\times L^H&1\\endbmatrix\\succeq0.\\)
令多项式\\(H(\\omega)\\)的振幅均匀有界(对所有\\(\\omega\\in[-\\pi,\\pi]\\)有\\(H(\\omega)\\leq\\gamma\\),其中\\(\\gamma \\in R_+\\)为给定正实数.作为有界三角多项式的特例,令\\(|B(\\omega)|=\\gamma\\),那么\\(H(\\omega)\\leq\\gamma\\)可以用两个线性不等式抽象,如下:(其中\\(R_B(\\omega)=\\gamma^2\\))
\\(\\beginbmatrix\\mathbfQ_L\\times L&\\mathbfh_L\\times1\\\\ \\mathbfh_1\\times L&1\\endbmatrix\\succeq0,\\\\ \\sum_i=1^L-jQ_i,i+j=\\left\\\\beginarrayc\\gamma^2,&j=0\\\\ 0,&j=1,\\cdots,L-1.\\endarray\\right.\\)
有界三角多项式的结果可以用于\\(\\infty\\)范数,因为多项式的最大振幅设置上界意味着多项式对所有\\(\\omega\\in[-\\pi,\\pi]\\)具有一致有界的振幅,即\\(\\beginarrayl\\|H\\|_\\infty=\\max\\limits_\\omega\\in[-\\pi,\\pi]|H(\\omega)|\\leq\\gamma,\\\\ |H(\\omega)|\\leq\\gamma,\\forall\\omega\\in[-\\pi,\\pi].\\endarray\\)
回到本节开始处,基于振幅一致有界条件和Schur补条件,对偶问题可以表征为以下凸优化问题:
\\(\\beginarrayc\\max\\operatornameRe\\left(\\mathbfc^H\\mathbfy-\\epsilon\\Vert c\\Vert_2\\right)~~\\operatornamesubject to\\left[\\beginarraycc\\mathbfQ_M\\times M&\\mathbfc_M\\times1\\\\ \\mathbfc_1\\times M&1\\endarray\\right]\\succeq0,\\\\ \\sum_i=1^M-j\\mathbfQ_i,i+j=\\left\\\\beginarraycc1,&j=0\\\\ 0,&j=1,\\cdots,M-1.\\endarray\\right.\\endarray\\)
代码
% 本处仅给出上述凸优化问题的核心代码[完整代码联系博主]
if noise_flag == 0 % 无噪声版本
cvx_begin sdp quiet
cvx_solver sdpt3
variable S(M+1,M+1) hermitian
subject to
S >= 0;
S(M+1,M+1) == 1;
trace(S) == 2; % 主对角元素迹为2
for j = 1 : M-1
sum(diag(S,j)) == S(M+1-j,M+1); % 非主对角线元素求和为0.
end
maximize (real(S(1:M,M+1)\'* Y)) % - 0.5 * norm(c)
cvx_end
else % noise version
regular_param = 0.2; % 有噪声需要引入正则化参数
cvx_begin sdp quiet
cvx_solver sdpt3
variable S(M+1,M+1) hermitian
subject to
S >= 0;
S(M+1,M+1) == 1;
trace(S) == 2;
for j = 1 : M - 1
sum(diag(S,j)) == S(M+1-j,M+1);
end
maximize (real(S(1:M,M+1)\'* Y) - regular_param * norm(c));
cvx_end
end
原子范数软阈值问题的推导
推导
原子集合由各个正弦曲线的样本组成,\\(a_f,\\phi\\in C^n\\),表示为\\(a_f,\\phi=e^i2\\pi\\phi\\left[1~e^i2\\pi f~\\cdots e^i2\\pi(n-1)f\\right]^T\\)
无限原子集\\(\\mathcalA=\\a_f,\\phi:f\\in[0,1],\\phi\\in[0,1]\\\\)组成了\\(x^*\\)适当的原子集合,\\(x^*\\)在对偶问题中可以写成一个稀疏的非负的原子组合。\\(x^\\star=\\sum_l=1^k c_l^\\star a_f_l^\\star,0=\\sum_l=1^k|c_l^\\star|a_f_l^\\star,\\phi_l\\),\\(c_l^\\star=|c_l^\\star|e^i2\\pi\\phi_l\\).
相应的对偶范数采用直观的形式:\\(\\|v\\|_\\mathcalA^*=\\sup\\limits_f,\\phi\\langle v,a_f,\\phi\\rangle=\\sup\\limits_f\\in[0,1]\\sup\\limits_\\phi\\in[0,1]e^i2\\pi\\phi\\sum\\limits_l=0^n-1v_l e^-2\\pi i l f=\\sup\\limits_|z|\\le1\\left|\\sum\\limits_l=0^n-1v_l z^l\\right|\\),\\(\\|v\\|_\\mathcalA^*\\)可以理解为在单位圆上获得的最大绝对值\\(\\zeta\\mapsto\\sum_l=0^n-1v_l\\zeta^l\\),\\(\\cal A=\\a_f,\\phi|f\\in[0,1],\\phi\\in[0,1]\\\\)为与线谱原子集相关的原子范数的半正定规划.
根据上式可知向量\\(v\\in C^n\\)的对偶原子范数是复数三角多项式\\(V(f)=\\sum_l=0^n-1v_l e^j2\\pi lf\\)的最大绝对值;因此,对对偶原子范数的约束等价于对\\(V(f)\\)大小的限制:\\(||v||_A^\\textt\\leq\\tau\\Leftrightarrow|V(f)|^2\\leq\\tau^2,\\forall f\\in[0,1]\\).函数\\(q(f)=\\tau^2-|V(f)|^2\\)是一个三角多项式,\\(q(f)\\)非负的充要条件是可以写成三角多项式的平方和.
定义映射\\(T:\\mathbbC^n\\to\\mathbbC^n\\times n\\),从输入创建一个Hermitian Toeplitz 矩阵,即\\(T(x)=\\beginbmatrixx_1&&x_2&&...&&x_n\\\\ x_2^*&&x_1&&...&&x_n-1\\\\ \\vdots&&\\vdots&&\\ddots&&\\vdots\\\\ x_n^*&&x_n-1^*&&...&&x_1\\endbmatrix\\).
对于给定的因果三角多项式\\(V(f)=\\sum_l=0^n-1v_le^-2\\pi i l f,\\)如果有且仅有复Hermitian矩阵\\(Q\\)存在时有\\(|V(f)|\\leq\\tau\\),这与原子范数对偶问题中第4节证明类似,即有\\(T^*(Q)=\\tau^2e_1~\\mathrmand~\\beginbmatrixQ&v\\\\ v^*&1\\endbmatrix\\succeq0.\\)其中\\(e_1=[1,0,0,....,0]^T\\),\\(v^*\\)表示\\(v\\)的Hermitian转置.
重写原子范数\\(\\Vert x \\Vert_A=\\sup_\\|v\\|_\\mathcalA^*\\leq1<x,v>\\)为下列形式:[\\(T^*\\)表示伴随矩阵]
\\(\\beginarrayll\\textmaximize_v,Q&\\langle x,v\\rangle\\\\ \\textsubject to&T^*(Q)=e_1\\\\ &\\beginbmatrixQ&v\\\\ v^*&1\\endbmatrix\\succeq0.\\endarray\\)
下面对上述问题进行对偶推导:
1、首先需要将上述问题转化为无约束的拉格朗日方程形式,可以表示如下:
$L(Q,v,u,\\Gamma)=\\langle x,v\\rangle +u^* T^* (Q)-u^He_1-\\Gamma \\beginbmatrixQ&v ;\\ v^*&1\\endbmatrix $
2、对变量\\(v\\)求解极值,则有\\(x- Tr(\\Gamma\\beginbmatrix0&I\\\\ I^*&0\\endbmatrix)=x- Tr(\\Gamma\\beginbmatrix\\Gamma_12I^*&\\Gamma_11I\\\\ \\Gamma_22I^*&\\Gamma_21I\\endbmatrix)=x-2\\Gamma_12=0\\),那么可以得到\\(\\Gamma_12=\\fracx2;\\)\\(\\Gamma_21=\\fracx^*2\\)
3、对变量\\(Q\\)求解极值前,先将\\(u^H T^*(Q)\\)进步抽象为\\(Tr(T(u)\\cdot Q)\\),那么关于\\(Q\\)的偏导可表示为\\(T(u)-\\Gamma\\beginbmatrixI&0\\\\ 0&0\\endbmatrix=0\\),那么则有\\(\\Gamma_11=T(u)\\),其中\\(F_22=t\\),用于半正定约束\\(\\Gamma=\\beginbmatrixT(u)&x/2\\\\ x^*/2&t\\endbmatrix\\geq0\\).
4、将\\(\\Gamma\\)结果代入到\\(L\\)中,那么有如下证明:
\\(L=Re(v^*x)+Tr(T(u)\\cdot Q)-u^*e_1-Tr(\\beginbmatrixT(u)Q+Re(v^*x)/2&x/2+T(u)v\\\\ tv^*+Re(Qx^*)/2&Re(x^*v)/2+t\\endbmatrix ) =-u^*e_1-t=-u_1-t\\).
根据半正定约束条件\\(T(u)t-xx^*/4\\geq0\\),通过对\\(u\\)和\\(t\\)缩放则有\\(2t\\cdot T(2u)-xx^*\\geq0\\)
这等价于将对应目标函数缩放为\\(-u_1/2-t/2\\),那么原问题的对偶形式可以表示如下:
\\(\\beginarrayl l\\mathrmminimize_t,u&\\frac12(t+u_1)\\\\ \\mathrmsubject~to&\\beginbmatrixT(u)&x\\\\ x^*&t\\endbmatrix\\succeq0.\\endarray\\)
那么对应有噪声版本下的原问题对偶函数可以表示如下:[\\(\\tau\\)表示正则参数]
\\(\\beginarrayll\\textminimize_t,u,x&\\frac12\\|x-y\\|_2^2+\\frac\\tau2(t+u_1)\\\\ \\textsubject to&\\beginbmatrixT(u)&x\\\\ x^*&t\\endbmatrix\\succeq0.\\endarray\\)
上述问题可以通过凸优化中的SDP解释器求解,但是计算复杂度较高,可以通过交替方向投影算子加速求解.
代码
交替方向投影算子
原子范数软阈值AST推导
向量和矩阵的范数Ax=b的误差分析
一、向量和矩阵的范数
范数用来度量向量和矩阵的大小。
1.1 向量的范数
- 定义

- 常用范数
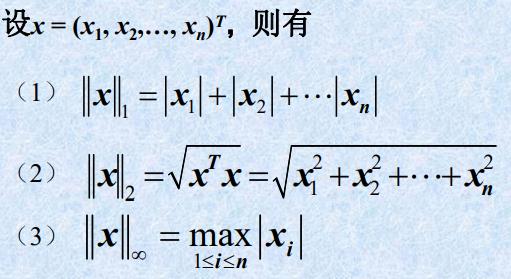
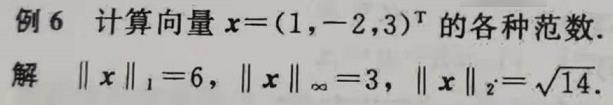
1.2 矩阵的范数
- 定义

- 定理


二、误差分析
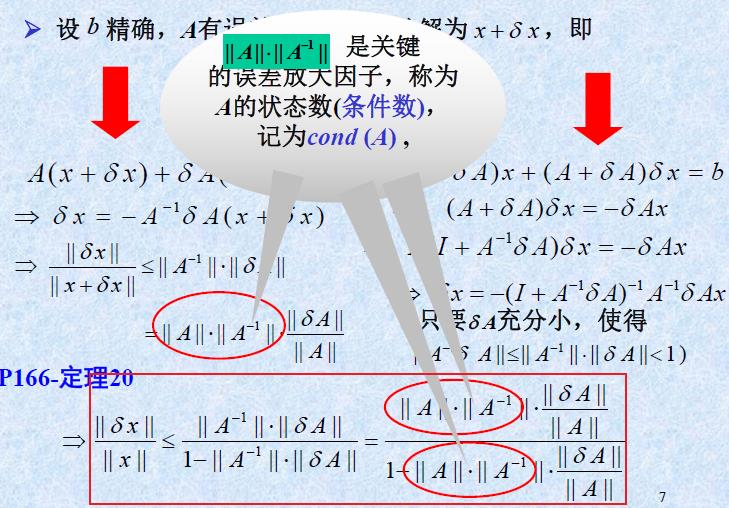
- 数据扰动
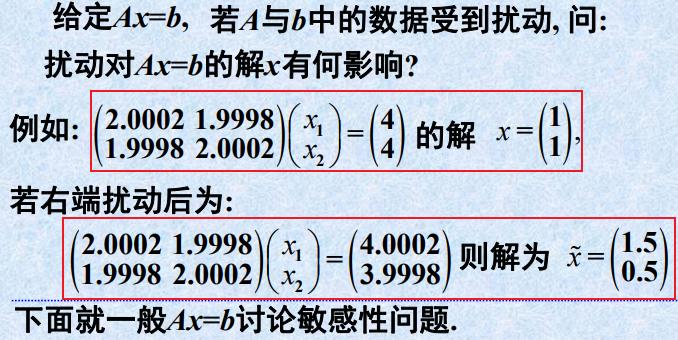

δ x = A − 1 δ b = > ∣ ∣ δ x ∣ ∣ < ∣ ∣ A − 1 ∣ ∣ ⋅ ∣ ∣ δ b ∣ ∣ \\delta x = A^-1 \\delta b => ||\\delta x|| < || A^-1|| · ||\\delta b|| δx=A−1δb=>∣∣δx∣∣<∣∣A−1∣∣⋅∣∣δb∣∣
∣ ∣ b ∣ ∣ = ∣ ∣ A x ∣ ∣ ||b|| = ||Ax|| ∣∣b∣∣=∣∣Ax∣∣ ≤ \\le ≤ ∣ ∣ A − 1 ∣ ∣ ⋅ ∣ ∣ x ∣ ∣ = > || A^-1|| · ||x|| => ∣∣A−1∣∣⋅∣∣x∣∣=> 1 ∣ ∣ x ∣ ∣ \\frac 1||x|| ∣∣x∣∣1 ≤ \\le ≤ ∣ ∣ A ∣ ∣ ∣ ∣ b ∣ ∣ \\frac ||A||||b|| ∣∣b∣∣∣∣A∣∣



总结
- 理论

以上是关于范数经典问题的推导与分析的主要内容,如果未能解决你的问题,请参考以下文章