svd,BD,ZF,SLNR,MMSE线性预编码性能对比MATLAB仿真

Posted 2023-04-16 51matlab

1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

 

 

 

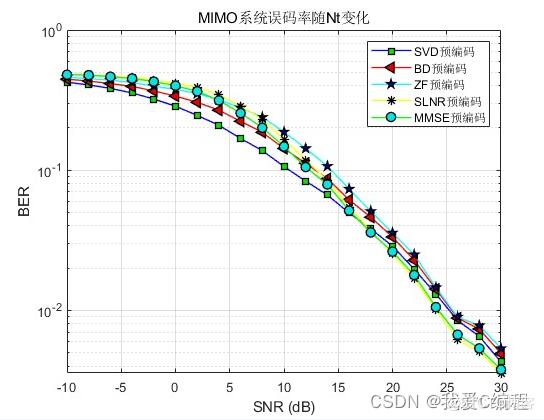
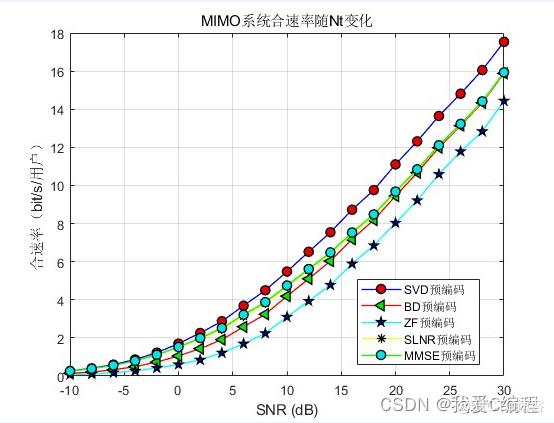
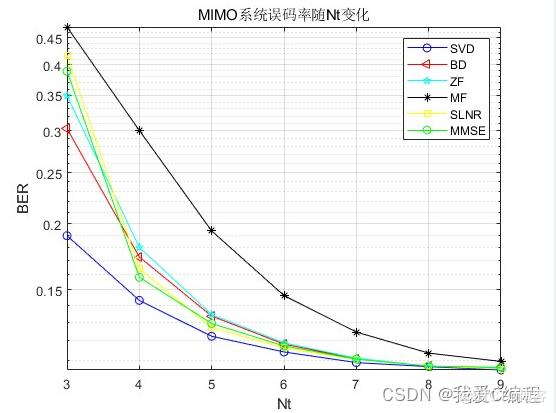
2.算法涉及理论知识概要

        线性预测编码（LPC）是主要用于音频信号处理与语音处理中根据线性预测模型的信息用压缩形式表示数字语音信号谱包络（en:spectral envelope）的工具。它是最有效的语音分析技术之一，也是低位速下编码方法高质量语音最有用的方法之一，它能够提供非常精确的语音参数预测。

 

       线性预测编码经常用来传输频谱包络信息，这样它就可以容忍传输误差。由于直接传输滤波器系数（参见线性预测中系数定义）对于误差非常敏感，所以人们不希望直接传输滤波器系数。换句话说，一个小的误差不会扭曲整个频谱或使整个频谱质量下降，但是一个小的误差可能使预测滤波器变得不稳定。有许多更加高级的表示方法，如对数面积比（en:log area ratio，LAR)、线谱对（en:line spectral pairs,LSP) 分解以及反射系数等。在这些方法中，LSP 由于它能够保证预测器的稳定性、并且小的系数偏差带来的谱误差也是局部的这些特性，所以得到了广泛应用。

 

2.1svd线性预编码

       单用户 SVD 预编码技术是一种点对点的 MIMO 系统，需要对发送端和接收端进行联合处理。 单用户 SVD 预编码技术利用了单用户 MIMO 信道的所有通道来传送信息，需要在发送端需要进行预编码，同时在接收端也要进行赋形处理。信道矩阵H的 SVD 分解为：

 

 

 

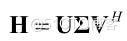
       其中 U 和 V 都是正交矩阵且Σ=diag(a1,a2,...)为对角矩阵。令发射信号x=Va，即发送预处理矩阵使用信道矩阵HSVD 分解后的右奇异矩阵V ，则处理机则用矩阵U来进行接收赋形，得:

 

 

 

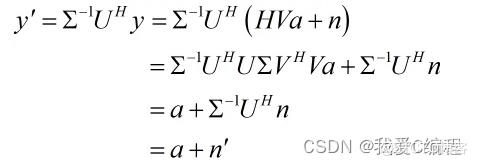
2.2BD线性预编码

        块对角化预编码是在多用户MIMO系统下行链路中受到广泛认可的一种线性预编码，它将多用户MIMO系统的下行信道矩阵分解为块对角化形式，等效为多个互不干扰的单用户MIMO系统，完全消除了用户间干扰，通过合理的功率分配，能获得比迫零线性预编码更高的系统容量。块对角化预编码是对 ZF 预编码算法的改进，它在线性预编码矩阵前乘入了零空间矩阵，可以有效减小其他用户产生的干扰。.

 

 

 

2.3ZF线性预编码

       ZF预编码可以理解为把user自身因为多天线空间信道传输而产生的在同时同频的自干扰消掉(但没有考虑消去高斯分布的noise)，从而最小化了真实信号和估计的误差平方和，而从统计来看就是Maximize likelihood这个模型

 

 

3.MATLAB核心程序

 

 %svd
            [W1,M1]=svdprecoding(H,K,S,P);
            [U,D,V]=svd(H);
            p1 = ones(1,K*S);
            % p1 = waterfilling(D,SNR,Nt,K,S);
           [count_temp] = receiver(H,Nt,S,K,Tc,P,n,W1,M1,s,q);
            count1=count1+count_temp;
            G=M1*H*W1;
            capacity1=capacity1+log2(det(eye(K*S,K*S)+P/(sigma2*Nt)*G*G\'));       
  % BD
            [W2,D2 M2] = BD2(Nt,Nri,S,K,H,P);
            p2 = ones(1,K*S);
            [count_temp] = receiver(H,Nt,S,K,Tc,P,n,W2,M2,s,q);
            count2=count2+count_temp;
            capacity2=capacity2+sumrate(H,W2,M2,K,S,Nri,Nt,sigma2,P);        
  %ZF
           [W3]=ZF(H,P,K,S);
           [count_temp] = receiver(H,Nt,S,K,Tc,P,n,W3,eye(K*Nri),s,q);
            count3=count3+count_temp;
            capacity3=capacity3+sumrate(H,W3,eye(K*Nri),K,S,Nri,Nt,sigma2,P);          
%SLNR
       %[W5]  = SLNR(Nt,Nri,S,K,H,sigma2,P);
        [W5]=SLNR2(H,sigma2,P,K,Nri,S,Nt);
        [count_temp] = receiver(H,Nt,S,K,Tc,P,n,W5,eye(K*Nri),s,q);
            count5=count5+count_temp;
     
       capacity5=capacity5+sumrate(H,W5,eye(K*Nri),K,S,Nri,Nt,sigma2,P);
%MMSE
        [W6,M6]=MMSE(H,sigma2,P,K,Nri,S,Nt);
        [count_temp] = receiver(H,Nt,S,K,Tc,P,n,W6,M6,s,q);
            count6=count6+count_temp;
        
       capacity6=capacity6+sumrate(H,W6,M6,K,S,Nri,Nt,sigma2,P);

 

　　

 

PythonPython 实现破零（ZF）和最小均方误差（MMSE）信道均衡

目录

• 1 理论
• 2 ZF均衡实现
• 3 MMSE均衡

1 理论

在无线通信中。 无线信道由各种类型的损伤组成，例如延迟扩展、衰落和多普勒扩展等。信道中的多径传播引入延迟扩展，导致 ISI、ICI等等问题，在信号接收端，我们需要进行均衡以减少失真，减轻 ISI 和噪声的综合影响。 因此为了恢复原始信号，使用滤波器，常用基本的滤波器有破零（Zero Forcing，ZF） 和最小均方误差（ Minimum Mean Square Error，MMSE）算法。

ZF算法使用一个加权矩阵W消除信道的干扰，根据估计的信道响应H初始化矩阵W
$$W_{ZF}=(H^{H}H{)}^{-1}{H}^H$$
则恢复的信号表示
$$\begin{gathered} \hat{y}=h\cdot x \\ \hat{z}=W_{ZF}\cdot \hat{y} \end{gathered}$$

其中x表示发送的信号,，h表示信道冲击响应，H是估计的信道冲击响应，z表示恢复的信号。

MMSE 均衡原理

略

2 ZF均衡实现

import numpy as np
from numpy.linalg import inv


# 此函数基于输入数组生成矩阵，偏移量offset基于输入数组
def generate_square_matrix(arr_data,size,data_offset,datatype):
    aMatrix = np.mat(np.zeros(shape=(size,size))).astype(datatype)
    for i1 in range(size):    
        for i2 in range(size):
            try:
                arr_index = i2+data_offset-i1
                if arr_index < 0:
                    continue
                aMatrix[i2,i1]=arr_data[arr_index]
            except:
                break
    return aMatrix
# 它取一个矩阵并将矩阵的中间列提取到一个数组中
def get_W_vector(inv_matrix, size,data_type):
    mid_col=size>>1
    C_vector=np.zeros(shape=(size)).astype(data_type)
    for i in range(size):
        C_vector[i]= inv_matrix[i,mid_col]
    return C_vector
def ZF_equalizer(y,h,size,size_of_input,data_type):
    ZF_h = generate_square_matrix(h,size,h.argmax(),data_type)
    ZF_h_hat = inv(ZF_h)
    ZF_W = get_W_vector(ZF_h_hat,size,data_type)
    z=np.convolve(y,ZF_W)
    leftside=size>>1
    # print("\\nReconstructed signal: \\n",z[leftside:leftside+size_of_input])    
    return z[leftside:leftside+size_of_input]


# 发送的信号
x = np.array([3-0.6j, -0.3+0.9j,
              0.1 - 1.2j, -0.7+0.2j,
              0+0.7j, -0.5+0.5j,
              0.1-0.6j, -0.4+0.6j])
# 信道冲击响应
h = np.array([1, 0, 0.3+0.3j])
H_exact = np.fft.fft(h)
# 仿真经过信号经过信道
y = np.convolve(x, h)

# 滤波器长度 
filter_length = 13
ZF_result = ZF_equalizer(y, h, filter_length, x.size, complex)
print("原始signal：", x)
print("恢复signal:", ZF_result)
plt.plot(abs(x))
plt.plot(abs(ZF_result))
plt.ylabel('$|Z|$')
plt.grid(True)
plt.savefig('signal.png')

发送信号和恢复信号是否一致,通过绘图可以看出,完全一致

3 MMSE均衡

仿真过程,需要安装pyphysim,执行pip install pyphysim

import numpy as np
from numpy.linalg import inv

# 此函数基于输入数组生成矩阵，偏移量offset基于输入数组
def generate_square_matrix(arr_data,size,data_offset,datatype):
    aMatrix = np.mat(np.zeros(shape=(size,size))).astype(datatype)
    for i1 in range(size):    
        for i2 in range(size):
            try:
                arr_index = i2+data_offset-i1
                if arr_index < 0:
                    continue
                aMatrix[i2,i1]=arr_data[arr_index]
            except:
                break
    return aMatrix
import matplotlib.pyplot as plt
from pyphysim.util.conversion import dB2Linear
from pyphysim.util.misc import pretty_time, randn_c
def MMSE_equalizer(x, y, size, data_type):
    # 计算自相关性
    ryy = np.correlate(y, y, "full")
    # 计算互相关性
    rxy = np.correlate(x, y, "full")

    #从 ryy 和向量 Rxy 形式 rxy 生成矩阵 Ryy
    Ryy = generate_square_matrix(ryy, size, ryy.argmax(), data_type)
    Rxy = np.mat(np.zeros(shape=(size, 1))).astype(data_type)
    # 计算偏移量
    offset = rxy.argmax() - (size >> 1)
    for i in range(size):Rxy[i, 0] = rxy[i+offset]
    MMSE_C_Vec = np.asarray(inv(Ryy)*Rxy).flatten()
    result = np.convolve(y, MMSE_C_Vec)
    leftside = size >> 1
    print("发送的signal: ", x)
    print("接收的signal:", y)
    print("恢复的signal:", result[leftside:leftside+x.size])
    return result[leftside:leftside+x.size]

x = np.array([0.73+0.59j, 0.43+1.01j, 0.41+0.3j, 1.24+1.1j, 0.55+0.83j])
SNR_dB = 30
snr_linear = dB2Linear(SNR_dB)
noise_power = 1 / snr_linear
# 噪声
n = np.math.sqrt(noise_power) * randn_c(x.size)
# 信道响应
h = randn_c(x.size)
#
y_z = h * x + n
# MMSE均衡
y_z /= h
print(y_z)
# 滤波器长度
filter_length = 1
z = MMSE_equalizer(x, y_z, filter_length, complex)

plt.plot(abs(x))
plt.plot(abs(z))
plt.grid(True)
plt.savefig('signal2.png')