三维海浪曲面的动态模拟matlab仿真

Posted 2023-04-16 51matlab

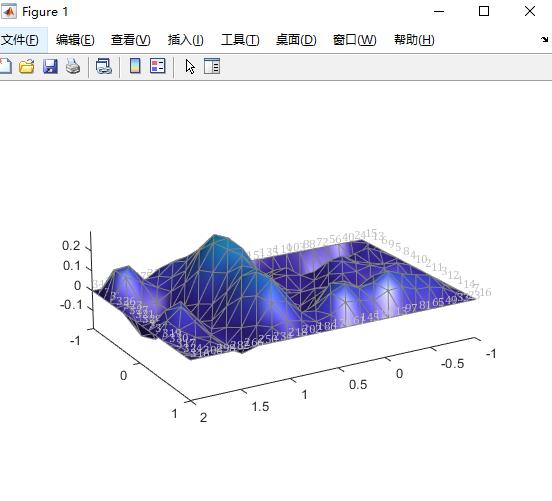
1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

 

2.算法涉及理论知识概要

       考虑到三维海浪波运动的高度、形状、频率以及方向随时的变化以及参考相关论文，基于海浪谱使用双叠加模型模拟出三维海浪图像，用matlab程序模拟出来的海浪的最大高度与风级关系符合实际资料，结果比较理想。

 

       海浪是属于统计范畴内的一种不确定的数量关系。当速度和方向一定的风在开阔的海面上吹拂是，海浪便从风中吸收能量同时随着波动而传递走能量，当这两方面的能量达到平衡时，此时海浪成为成熟期海浪，根据随机过程理论，此时海浪可以看作是一种平稳随机过程。于是可以用平稳随机过程理论来分析海浪。实际海面上的海浪是极为复杂的，它是不规则的随机波。为了研究方便，可以把海浪简化为长峰波海浪，即海浪只沿一个固定的方向前进，每个垂直于波浪前进方向的波线是无限长的且波峰彼此保持平行。

 

       根据水波理论，不规则的长峰波海浪可以看成由无数个不同波幅和波长的余弦波叠加而成。考虑海面上的固定点波浪，则定点长峰波海浪的方程可表示为：

 

 

 

 

       对于一定的海面情况，其对应的波谱密度具有一定形式。能谱公式可以从海上实测得到，亦可根据理论和经验的关系导出。国际上描述海浪的谱密度公式有多种，如BTTP波普、史考特波普、劳曼波普、PM波普、ISSC波普等。这里采用ITTC双参数谱，它是PM波普的派生形式，适用于成熟期海浪，以有义波高和海浪特征周期为谱参量，以成熟期海浪观测资料为依据，谱结构简单，第十一届国际船模水池会议将该谱定为标准海浪谱，其形式如下：

 

 

 

 

 

 

 

        理论上海浪平铺的分布频率为，但仿真时不可能对所有频率的谐波进行仿真，只能取其影响较大的频段来仿真，另外，由于各种海浪的频谱都是狭带谱，它们的能量更是集中在某一频段，选取某一频段中的有限个谐波进行仿真，结果仍可以保持较高的精确度。对于海浪的仿真，通常有三种方法：频率等分法、有理谱法、和能量等分法。由于频率等分法计算简单，实时性较好，因此这里选用频率等分法进行海浪仿真。将海浪谱分解成30级谐波。仿真频段取为，采样频率增量为确定各仿真频率，，﹒﹒﹒,，后便可以计算出相应的频谱，，﹒﹒﹒，和海浪每个谐波的幅值。

 

3.MATLAB核心程序

 

 % First half step
     
         % x direction
         i = 1:n+1;
         j = 1:n;
     
         % height
         Hx(i,j) = (H(i+1,j+1)+H(i,j+1))/2 - dt/(2*dx)*(U(i+1,j+1)-U(i,j+1));
     
         % x momentum
         Ux(i,j) = (U(i+1,j+1)+U(i,j+1))/2 -  ...
                   dt/(2*dx)*((U(i+1,j+1).^2./H(i+1,j+1) + g/2*H(i+1,j+1).^2) - ...
                              (U(i,j+1).^2./H(i,j+1) + g/2*H(i,j+1).^2));
     
         % y momentum
         Vx(i,j) = (V(i+1,j+1)+V(i,j+1))/2 - ...
                   dt/(2*dx)*((U(i+1,j+1).*V(i+1,j+1)./H(i+1,j+1)) - ...
                              (U(i,j+1).*V(i,j+1)./H(i,j+1)));
         
         % y direction
         i = 1:n;
         j = 1:n+1;
    
         % height
         Hy(i,j) = (H(i+1,j+1)+H(i+1,j))/2 - dt/(2*dy)*(V(i+1,j+1)-V(i+1,j));
     
         % x momentum
         Uy(i,j) = (U(i+1,j+1)+U(i+1,j))/2 - ...
                   dt/(2*dy)*((V(i+1,j+1).*U(i+1,j+1)./H(i+1,j+1)) - ...
                              (V(i+1,j).*U(i+1,j)./H(i+1,j)));
         % y momentum
         Vy(i,j) = (V(i+1,j+1)+V(i+1,j))/2 - ...
                   dt/(2*dy)*((V(i+1,j+1).^2./H(i+1,j+1) + g/2*H(i+1,j+1).^2) - ...
                              (V(i+1,j).^2./H(i+1,j) + g/2*H(i+1,j).^2));
     
         % Second half step
         i = 2:n+1;
         j = 2:n+1;
     
         % height
         H(i,j) = H(i,j) - (dt/dx)*(Ux(i,j-1)-Ux(i-1,j-1)) - ...
                           (dt/dy)*(Vy(i-1,j)-Vy(i-1,j-1));
         % x momentum
         U(i,j) = U(i,j) - (dt/dx)*((Ux(i,j-1).^2./Hx(i,j-1) + g/2*Hx(i,j-1).^2) - ...
                           (Ux(i-1,j-1).^2./Hx(i-1,j-1) + g/2*Hx(i-1,j-1).^2)) ...
                         - (dt/dy)*((Vy(i-1,j).*Uy(i-1,j)./Hy(i-1,j)) - ...
                           (Vy(i-1,j-1).*Uy(i-1,j-1)./Hy(i-1,j-1)));
         % y momentum
         V(i,j) = V(i,j) - (dt/dx)*((Ux(i,j-1).*Vx(i,j-1)./Hx(i,j-1)) - ...
                           (Ux(i-1,j-1).*Vx(i-1,j-1)./Hx(i-1,j-1))) ...
                         - (dt/dy)*((Vy(i-1,j).^2./Hy(i-1,j) + g/2*Hy(i-1,j).^2) - ...
                           (Vy(i-1,j-1).^2./Hy(i-1,j-1) + g/2*Hy(i-1,j-1).^2));

 

　　

 

有限元动态水波模拟基于有限元的三维动态水波运动模拟matlab仿真

1.软件版本

MATLAB2021a

2.核心代码

% Finite element solution of wave equation
 
close all;
load meshdata;
% c(x,y)===================================================================
c=@(X)1;
% =========================================================================
numberofnodes=size(p,1);
numberofelements=size(t,1);
% Initialisation of K, M ==================================================
K=zeros(numberofnodes,numberofnodes);
M=zeros(numberofnodes,numberofnodes);
% Computation of Ke, Me & assemby of K, M==================================
for e=1:numberofelements
   nodes=t(e,:); % row with nodenumbers of element e
   P=[ones(1,3);p(nodes,:)'];
   Coeffs=inv(P);
   areaelemente=abs(det(P))/2; % area of element e
   diffPhi=Coeffs(:,2:end);
   Ke=diffPhi*diffPhi'*areaelemente;
   Me=1/3^2*ones(3)*1/(c(mean(p(nodes,:))))^2*areaelemente;
   K(nodes,nodes)=K(nodes,nodes)+Ke;
   M(nodes,nodes)=M(nodes,nodes)+Me;
end
Mlumped=diag(M(1:size(M,1)+1:end));
M=Mlumped;
% Dirichlet boundaries=====================================================
% =unique(boundedges(p,t));
Dirichlet=[

...............................................

3.操作步骤与仿真结论

 5.参考文献

[1]杨永丰, 王玉玮, 樊瑜波. 三维有限元动态分析方法的建立[C]// 中华口腔医学会第三次全国口腔修复学术会议. 0.

D215

6.完整源码获得方式

方式1：微信或者QQ联系博主

方式2：订阅MATLAB/FPGA教程，免费获得教程案例以及任意2份完整源码