Python实现计算器
Posted ZingpLiu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python实现计算器相关的知识,希望对你有一定的参考价值。
前几天有个面试题目:计算字符串"1 + (5 - 2) * 3",结果为10,不能用eval()。今天介绍一下用压栈的方法解一解这个题目,事实上我们的计算器原理也是如此。
1 分析题目
(1)如果计算“1+2”这种两个数之间的运算,比较简单,可直接将“字符数字”1,2分解出来,强制转换为float类型,然后根据中间的运算符加减乘除就行。这题难在需要再复杂的算式中考虑运算符有优先级。
(2)通常我们在计算的时候,实际上也是不断进行两个数之间运算,并将算完的结果再和其他数进行运算。比如“1 + 2 + 4”,第一步先算出1+2=3之后,再用算出的结果3和4相加,得到最终结果7。
(3)如果我们能够将算式“1+2+4”,看做是一个处理好的列表:
将字符串算式 "1+2+4" 处理成: [\'1\', \'+\', \'2\', \'+\', \'4\']
那么我们可以通过压栈的方式计算出结果。首先设置两个列表(栈),分别存放 数字 和 运算符,然后遍历 [\'1\', \'+\', \'2\', \'+\', \'4\']:
遍历 处理过的算式列表:[\'1\', \'+\', \'2\', \'+\', \'4\'] 第一次: 得到数字\'1\', 转换成float, 放入数字栈: 数字栈: [1.0, ] 运算符栈: [ ] 第二次: 得到运算符\'+\',放入运算符栈: 数字栈:[1.0, ] 运算符栈:[\'+\', ] 第三次: 得到数字\'2\',转换成float, 放入数字栈: 数字栈:[1.0, 2.0] 运算符栈:[\'+\', ] 第四次: 得到运算符\'+\', 此时应注意: 运算符栈的最后一位也是\'+\'号, 现在又来了一个\'+\'号,说明相邻两个运算符的优先级别是一样的。 既然优先级别是一样的,四则运算法则告诉我们应该从左往右计算对吧?所以,此处不再一味地将运算符\'+\'入栈。而是: (1)弹出数字栈中的最后两位数字,即 2.0 和 1.0 ; (2)弹出运算符栈中的最后一个运算符\'+\'; (3)将弹出的数字和运算之间进行计算,即计算 2.0 + 1.0 = 3.0; (4)将3.0放入数字栈,代替之前的 1.0 和 2.0; 即: 数字栈:[3.0, ] 运算符栈:[ ] 别忘了,我们第四次得到的运算符\'+\'号,此时, 如果运算符栈中,弹出上一次运算过的运算符\'+\'之后,还有别的运算符, 那么我们还应该将运算符栈的最后一个运算符 和 本次得到的运算符 \'+\' 进行比较,判断是否是同一级别。 如果同一级别还得继续弹栈,继续运算。不在同一级别那就应该将运算符入栈。 而现在,我们的运算符栈已经空了,那么应该把运算符\'+\'放入运算符栈,即: 数字栈:[3.0, ] 运算符栈:[\'+\', ] 这样第四次才算大功告成。 第五次: 得到数字\'4\',转换成float, 放入数字栈: 数字栈:[3.0, 4.0] 运算符栈:[\'+\', ] 至此我们已经遍历完算式列表:[\'1\', \'+\', \'2\', \'+\', \'4\'],但在数字栈和运算符栈中还有元素。 那么我们应该依次弹出最后两个数字4.0 和3.0,以及最后一个运算符\'+\',然后进行运算,得到7.0,并代替原来数字栈中的4.0 和3.0,即: 数字栈:[7.0, ] 运算符栈:[ ] 最后得到的最终结果就是数字栈中的第一位元素:7.0。
通过描述计算 "1+2+4" 的过程,我们总结出这一方法计算的两个重点:
第一个重点:把算式处理成列表形式。如:\'-1-2*((-2+3)+(-2/2))\' 应该处理成:[\'-1\', \'-\', \'2\', \'*\', \'(\', \'(\', \'-2\', \'+\', \'3\', \')\', \'+\', \'(\', \'-2\', \'/\', \'2\', \')\', \')\'] 。
第二个重点:建立两个栈,数字栈和运算符栈。遍历算式列表,(从前往后取出列表中的元素),将数字放入数字栈,将运算符放入运算符栈。但是,需要通过运算符栈中的最后一个运算符 与 当前拿到的运算符 比较,判断出应该弹栈进行运算还是直接入栈。
2 总结算法
通过1中的分析我们大致可以整理出如下算法:
1 将算式整理成列表formula_list。 2 循环[为方便描述,我们把此处循环叫循环1],依次取出列表中的元素 e (element缩写)。 if e 是数字: 加入数字栈num_stack,获取下一个元素e。 else e 不是数字(即是运算符): while True:(不断循环,此处是为了不断比较从算式列表中拿到的运算符和运算符栈中的最后一个运算符的优先级) 如果运算符栈op_stack 为空: 运算符 e 无条件加入运算符栈,并获取下一个元素e 如果运算符栈不为空: 取出运算符栈最后一个运算符 和 当前运算符e比较,得出一个决策。决策分为[入栈,出栈,0]三种。 如果决策是入栈: 将运算符加入运算符栈,并获取下一个元素e 如果决策是出栈: 弹出数字栈中的最后两位数字,运算符栈中的最后一个运算符。 计算,把结果代替原来的数字。 回退到while True循环 如果决策是0,这种情况专门表示运算符栈的最后一个元素是"(" 而当前获取到的元素是 ")": 弹出运算符栈中的最后一个运算符"(",并丢掉当前元素是")",获取下一个元素 3 上述处理完之后可能会存在一个问题: 当决策是0的时候,我们 弹出运算符栈中的最后一个运算符"(",并丢掉当前元素是")",获取下一个元素; 如果这个时候算式列表没有下一个元素了呢?此时既没有下一个元素,也没有继续运算,【循环1】结束了,但数字栈和运算符栈中可能还有元素。且运算符一定是同一级别的。 所以应该不断弹栈做运算,直到运算符栈中没有运算符为止。最后得到的结果就是数字栈的第一位元素。
以上分析我们抽象出几个函数:
(1)弹栈时计算‘两个数字和运算符组成的算式’结果的函数。
(2)判断元素是数字还是运算符的函数。
(3)把算式处理成列表形式的函数。如:\'-1-2*((-2+3)+(-2/2))\' 应该处理成:[\'-1\', \'-\', \'2\', \'*\', \'(\', \'(\', \'-2\', \'+\', \'3\', \')\', \'+\', \'(\', \'-2\', \'/\', \'2\', \')\', \')\'] 。
(4)决策函数,决定应该是入栈,弹栈运算,还是弹栈丢弃。
(5)主函数,遍历算式列表,计算最终结果。
3 两数运算函数
传入两个数字,一个运算符,根据运算符不同返回相应结果。即计算加减乘除:
def calculate(n1, n2, operator):
\'\'\'
:param n1: float
:param n2: float
:param operator: + - * /
:return: float
\'\'\'
result = 0
if operator == "+":
result = n1 + n2
if operator == "-":
result = n1 - n2
if operator == "*":
result = n1 * n2
if operator == "/":
result = n1 / n2
return result
4 判断是运算符还是数字
这里可能会想到isdigit()判断数字,但这个函数不能判断小数和负数。所以,我们自己写一个函数判断是否是运算符:
# 判断是否是运算符,如果是返回True
def is_operator(e):
\'\'\'
:param e: str
:return: bool
\'\'\'
opers = [\'+\', \'-\', \'*\', \'/\', \'(\', \')\']
return True if e in opers else False
5 格式化算式为列表
这个步骤需要处理的是区分横杠‘-’是代表负数还是减号。详细参见下例,注释已经十分明了:
# 将算式处理成列表,解决横杠是负数还是减号的问题
def formula_format(formula):
# 去掉算式中的空格
formula = re.sub(\' \', \'\', formula)
# 以 \'横杠数字\' 分割, 其中正则表达式:(\\-\\d+\\.?\\d*) 括号内:
# \\- 表示匹配横杠开头; \\d+ 表示匹配数字1次或多次;\\.?表示匹配小数点0次或1次;\\d*表示匹配数字1次或多次。
formula_list = [i for i in re.split(\'(\\-\\d+\\.?\\d*)\', formula) if i]
# 最终的算式列表
final_formula = []
for item in formula_list:
# 第一个是以横杠开头的数字(包括小数)final_formula。即第一个是负数,横杠就不是减号
if len(final_formula) == 0 and re.search(\'^\\-\\d+\\.?\\d*$\', item):
final_formula.append(item)
continue
if len(final_formula) > 0:
# 如果final_formal最后一个元素是运算符[\'+\', \'-\', \'*\', \'/\', \'(\'], 则横杠数字不是负数
if re.search(\'[\\+\\-\\*\\/\\(]$\', final_formula[-1]):
final_formula.append(item)
continue
# 按照运算符分割开
item_split = [i for i in re.split(\'([\\+\\-\\*\\/\\(\\)])\', item) if i]
final_formula += item_split
return final_formula
6 决策弹栈还是入栈
这个函数比较难,也比较抽象。比较连续两个运算符来判断是入栈还是弹栈:
def decision(tail_op, now_op):
\'\'\'
:param tail_op: 运算符栈的最后一个运算符
:param now_op: 从算式列表取出的当前运算符
:return: 1 代表弹栈运算,0 代表弹运算符栈最后一个元素, -1 表示入栈
\'\'\'
# 定义4种运算符级别
rate1 = [\'+\', \'-\']
rate2 = [\'*\', \'/\']
rate3 = [\'(\']
rate4 = [\')\']
if tail_op in rate1:
if now_op in rate2 or now_op in rate3:
# 说明连续两个运算优先级不一样,需要入栈
return -1
else:
return 1
elif tail_op in rate2:
if now_op in rate3:
return -1
else:
return 1
elif tail_op in rate3:
if now_op in rate4:
return 0 # ( 遇上 ) 需要弹出 (,丢掉 )
else:
return -1 # 只要栈顶元素为(,当前元素不是)都应入栈。
else:
return -1
7 主函数
主函数负责遍历算式列表中的字符,决定入数字栈或运算符栈或弹栈运算。
def final_calc(formula_list):
num_stack = [] # 数字栈
op_stack = [] # 运算符栈
for e in formula_list:
operator = is_operator(e)
if not operator:
# 压入数字栈
# 字符串转换为符点数
num_stack.append(float(e))
else:
# 如果是运算符
while True:
# 如果运算符栈等于0无条件入栈
if len(op_stack) == 0:
op_stack.append(e)
break
# decision 函数做决策
tag = decision(op_stack[-1], e)
if tag == -1:
# 如果是-1压入运算符栈进入下一次循环
op_stack.append(e)
break
elif tag == 0:
# 如果是0弹出运算符栈内最后一个(,丢掉当前),进入下一次循环
op_stack.pop()
break
elif tag == 1:
# 如果是1弹出运算符栈内最后一个运算符,弹出数字栈内后两个元素。
op = op_stack.pop()
num2 = num_stack.pop()
num1 = num_stack.pop()
# 执行计算
# 计算之后压入数字栈
num_stack.append(calculate(num1, num2, op))
# 处理大循环结束后 数字栈和运算符栈中可能还有元素 的情况
while len(op_stack) != 0:
op = op_stack.pop()
num2 = num_stack.pop()
num1 = num_stack.pop()
num_stack.append(calculate(num1, num2, op))
return num_stack, op_stack
8 终极代码与测试
import re
def calculate(n1, n2, operator):
\'\'\'
:param n1: float
:param n2: float
:param operator: + - * /
:return: float
\'\'\'
result = 0
if operator == "+":
result = n1 + n2
if operator == "-":
result = n1 - n2
if operator == "*":
result = n1 * n2
if operator == "/":
result = n1 / n2
return result
# 判断是否是运算符,如果是返回True
def is_operator(e):
\'\'\'
:param e: str
:return: bool
\'\'\'
opers = [\'+\', \'-\', \'*\', \'/\', \'(\', \')\']
return True if e in opers else False
# 将算式处理成列表,解决横杠是负数还是减号的问题
def formula_format(formula):
# 去掉算式中的空格
formula = re.sub(\' \', \'\', formula)
# 以 \'横杠数字\' 分割, 其中正则表达式:(\\-\\d+\\.?\\d*) 括号内:
# \\- 表示匹配横杠开头; \\d+ 表示匹配数字1次或多次;\\.?表示匹配小数点0次或1次;\\d*表示匹配数字1次或多次。
formula_list = [i for i in re.split(\'(\\-\\d+\\.?\\d*)\', formula) if i]
# 最终的算式列表
final_formula = []
for item in formula_list:
# 第一个是以横杠开头的数字(包括小数)final_formula。即第一个是负数,横杠就不是减号
if len(final_formula) == 0 and re.search(\'^\\-\\d+\\.?\\d*$\', item):
final_formula.append(item)
continue
if len(final_formula) > 0:
# 如果final_formal最后一个元素是运算符[\'+\', \'-\', \'*\', \'/\', \'(\'], 则横杠数字不是负数
if re.search(\'[\\+\\-\\*\\/\\(]$\', final_formula[-1]):
final_formula.append(item)
continue
# 按照运算符分割开
item_split = [i for i in re.split(\'([\\+\\-\\*\\/\\(\\)])\', item) if i]
final_formula += item_split
return final_formula
def decision(tail_op, now_op):
\'\'\'
:param tail_op: 运算符栈的最后一个运算符
:param now_op: 从算式列表取出的当前运算符
:return: 1 代表弹栈运算,0 代表弹运算符栈最后一个元素, -1 表示入栈
\'\'\'
# 定义4种运算符级别
rate1 = [\'+\', \'-\']
rate2 = [\'*\', \'/\']
rate3 = [\'(\']
rate4 = [\')\']
if tail_op in rate1:
if now_op in rate2 or now_op in rate3:
# 说明连续两个运算优先级不一样,需要入栈
return -1
else:
return 1
elif tail_op in rate2:
if now_op in rate3:
return -1
else:
return 1
elif tail_op in rate3:
if now_op in rate4:
return 0 # ( 遇上 ) 需要弹出 (,丢掉 )
else:
return -1 # 只要栈顶元素为(,当前元素不是)都应入栈。
else:
return -1
def final_calc(formula_list):
num_stack = [] # 数字栈
op_stack = [] # 运算符栈
for e in formula_list:
operator = is_operator(e)
if not operator:
# 压入数字栈
# 字符串转换为符点数
num_stack.append(float(e))
else:
# 如果是运算符
while True:
# 如果运算符栈等于0无条件入栈
if len(op_stack) == 0:
op_stack.append(e)
break
# decision 函数做决策
tag = decision(op_stack[-1], e)
if tag == -1:
# 如果是-1压入运算符栈进入下一次循环
op_stack.append(e)
break
elif tag == 0:
# 如果是0弹出运算符栈内最后一个(, 丢掉当前),进入下一次循环
op_stack.pop()
break
elif tag == 1:
# 如果是1弹出运算符栈内最后两个元素,弹出数字栈最后两位元素。
op = op_stack.pop()
num2 = num_stack.pop()
num1 = num_stack.pop()
# 执行计算
# 计算之后压入数字栈
num_stack.append(calculate(num1, num2, op))
# 处理大循环结束后 数字栈和运算符栈中可能还有元素 的情况
while len(op_stack) != 0:
op = op_stack.pop()
num2 = num_stack.pop()
num1 = num_stack.pop()
num_stack.append(calculate(num1, num2, op))
return num_stack, op_stack
if __name__ == \'__main__\':
formula = "1 - 2 * ( (60-30 +(-40/5) * (9-2*5/3 + 7 /3*99/4*2998 +10 * 568/14 )) - (-4*3)/ (16-3*2))"
print("算式:", formula)
formula_list = formula_format(formula)
result, _ = final_calc(formula_list)
print("计算结果:", result[0])
# 算式: 1 - 2 * ( (60-30 +(-40/5) * (9-2*5/3 + 7 /3*99/4*2998 +10 * 568/14 )) - (-4*3)/ (16-3*2))
# 计算结果: 2776672.6952380957
我们看一下谷歌运算的结果:
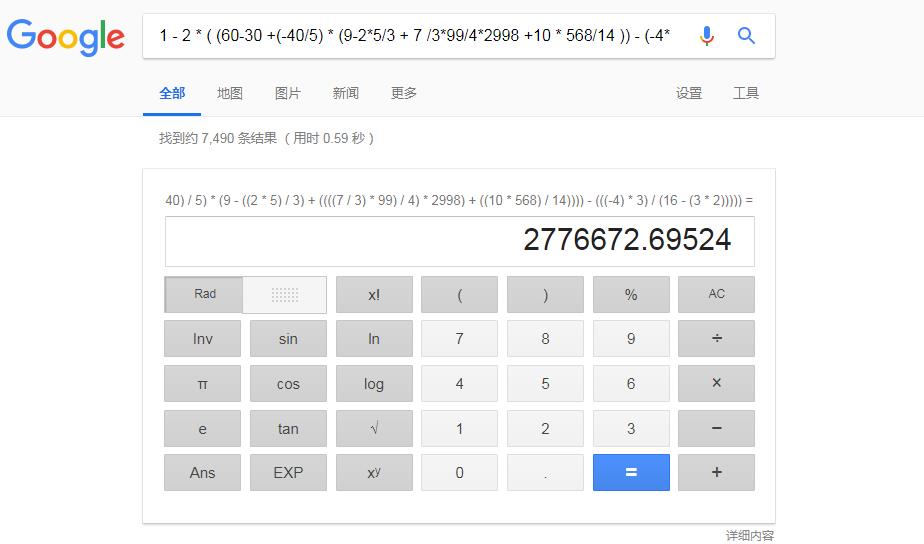
说明咱们算对了,不妨多测试一些算式看看。
本篇完。
以上是关于Python实现计算器的主要内容,如果未能解决你的问题,请参考以下文章