Shortest Cycle in a Graph

Posted 2023-04-14 onlyblues

Shortest Cycle in a Graph

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [u_i, v_i] denotes an edge between vertex u_i and vertex v_i . Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

Return the length of the shortest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.

Example 1:

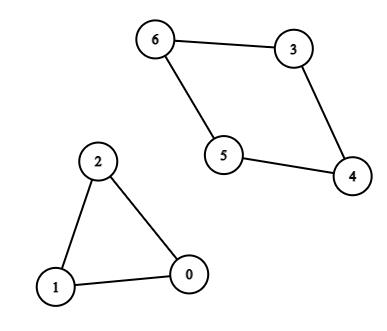
Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
Output: 3
Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0 

Example 2:

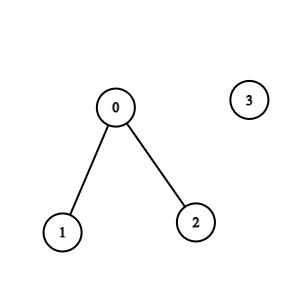
Input: n = 4, edges = [[0,1],[0,2]]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

• $2 \\leq n \\leq 1000$
• $1 \\leq \\textedges.length \\leq 1000$
• $\\textedges[i]\\text.length \\ \\mathrm== \\ 2$
• $0 \\leq u_i, v_i < n$
• $u_i \\ne v_i$
• There are no repeated edges.

 

解题思路

　　求最小环的模板题，当时比赛的时候没了解过就没做出来。解决最小环问题可以参考该博客：无向图的最小环问题。

　　可以发现题目中的$n$最大可以取到$1000$，因此不可以用Floyd的做法。又发现每一条边的权重都为$1$，因此可以枚举每一条边，然后删除这条边，再用bfs来求这条边两个端点间的最短路。这样就能得到包含这条边的环的最小长度。

　　AC代码如下，时间复杂度为$O(m(n+m))$：

 class Solution 
 public:
     int findShortestCycle(int n, vector<vector<int>>& edges) 
         vector<vector<int>> g(n);
         for (auto &p : edges) 
             g[p[0]].push_back(p[1]);
             g[p[1]].push_back(p[0]);
         
         int ret = 0x3f3f3f3f;
         for (auto &p : edges) 
             vector<int> dist(n, 0x3f3f3f3f);
             dist[p[0]] = 0;
             queue<int> q(p[0]);
             while (!q.empty()) 
                 int t = q.front();
                 q.pop();
                 for (auto &i : g[t]) 
                     if (t == p[0] && i == p[1] || i == p[0] && t == p[1]) continue;
                     if (dist[i] > dist[t] + 1) 
                         dist[i] = dist[t] + 1;
                         q.push(i);
                     
                 
             
             ret = min(ret, dist[p[1]] + 1);
         
         if (ret == 0x3f3f3f3f) ret = -1;
         return ret;
     
 ;

 

参考资料

　　最小环 - OI Wiki：https://oi-wiki.org/graph/min-circle/

本文来自博客园，作者：onlyblues，转载请注明原文链接：https://www.cnblogs.com/onlyblues/p/17319160.html

c_cpp find_all_cycle_in_graph_dfs

// 输出图中的所有的环
//color label :white(not visited),black(all children have been visited),gray(start visiting node)
// if one edge direct to a gray node means has cycle.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+3;
vector<int>g[maxn];
int vis[maxn];//0 while,1 gray, 2 black
int father[maxn];

void dfs(int u,int father) {
    vis[u] = 1;
    for (auto v:g[u]) {
        if (v == father) continue;
        if (!vis[v]) dfs(v, (fa[v] = u));
        else if (vis[v] == 1) {
            int tmp = u;
            while (tmp != v) {
                printf("%d->", tmp);
                tmp = fa[tmp];
            }
            printf("%d->%d\n", tmp, u);
        }
    }
    vis[u] = 2;
}
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < maxn; i++)
        vis[i] = 0, father[i] = -1, g[i].clear();
    for (int i = 0; i < m; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    int root = 1;
    dfs(1,-1); // 连通图
}

/*
* Sample input:
8 9
1 3
3 6
3 7
6 7
1 2
2 4
2 5
5 8
4 8
 
* Sample output
Cycle: 7->6->3->7
Cycle: 5->8->4->2->5
 
*/