[深入推导]CS231N assignment 2#4 _ 卷积神经网络 学习笔记 & 解析
Posted 360MEMZ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[深入推导]CS231N assignment 2#4 _ 卷积神经网络 学习笔记 & 解析相关的知识,希望对你有一定的参考价值。
卷积神经网络
基本算法实现
卷积神经网络应该算是图像处理中绝对的主流了, 关于算法得基本思想我在之前也学的比较懂了, 这点如果不了解网上有很多教程.
不过我并没有用代码亲自实现它. 我们首先确定怎么编写. 前面搞全连接网络总是会想着怎么去简化运算, 现在我们接触了新的网络, 要实现基础版本反而又不大适应了. 但是既然不要求计算准确性,那不就是一个一个像素填充么. (后面也没有要求我们用没有for循环版本,估计应该是太难了吧)

我们已经明白, 卷积本质上就是矩阵得内积, 对图像三通道相加之后加上偏置项. 所以算法上就是矩阵切片和相乘. 下面我们确定输出得规模和细节. 在作业注释中,已经说明:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- \'stride\': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- \'pad\': The number of pixels that will be used to zero-pad the input.
Returns a tuple of:
- out: Output data, of shape (N, F, H\', W\') where H\' and W\' are given by
H\' = 1 + (H + 2 * pad - HH) / stride # 更准确应当是整除
W\' = 1 + (W + 2 * pad - WW) / stride
- cache: (x, w, b, conv_param)也就是说: 输入图像为: 图片数目,通道数, 高,宽; 卷积核为每个通道得卷积核数目, 通道数目, 卷积核得高和宽. stride和padding由参数指定. 随后, 我们从padding后得左上角开始移动, 直到移动stride长度后会超出边界为止.由此就可以得到规模得计算公式了.
下面就是算法本体.
N, C, H, W = x.shape # 获取shape信息
F, C, HH, WW = w.shape
stride, pad = conv_param[\'stride\'], conv_param[\'pad\'] # 读取参数
# 整除
H_out = 1 + (H + 2 * pad - HH) // stride
W_out = 1 + (W + 2 * pad - WW) // stride
# 预先分配
out = np.zeros((N, F, H_out, W_out)) # 确定输出规模
# 只对图像本体扩充,即第三和第四维度,利用0填充
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), mode=\'constant\', constant_values=0)
for i in range(N): # 对于第i幅图片
for f in range(F): # 对于第f个卷积核(per 通道)
for j in range(H_out): # 高
for k in range(W_out): # 宽
out[i, f, j, k] = np.sum(
x_pad[i, :, j * stride: HH + j * stride, k * stride: WW + k * stride] * w[f],axis=None) + b[f]
# 切片参数:第i张图片,全部通道,从j*stride开始到ans+HH, 与整个w逐个元素相乘并直接求和卷积的图像意义
原始作业中用一种有趣的方式揭示了卷积运算的内涵. 在图像处理的学习中, 我们曾接触过sobel算子, 其可以用于边缘检测. 它就是通过特定的卷积核实现的.


这个作业通过RGB通道权重1:6:3混合, 并设置w为Gy的sobel算子,. 强化了y向边缘. 结果如下:

梯度下降
别忘了我们是naive版本的, 所以我们可以逐个像素逐个像素求解的. 为此我们列出这个像素和w,x的那些位置有关, 结合表达式求导. 请注意,下面的分析我们都是先对X做padding处理, 在进行计算的.

所以代码也就出来了:
x, w, b, conv_param = cache # 取出数据
N, C, H, W = x.shape
F, C, HH, WW = w.shape
stride, pad = conv_param[\'stride\'], conv_param[\'pad\']
N, F, H_out, W_out = dout.shape
# 先对X填充0
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), mode=\'constant\', constant_values=0)
# 预分配
dx = np.zeros_like(x)
dx_pad = np.zeros_like(x_pad)
dw = np.zeros_like(w)
db = np.zeros_like(b)
for i in range(N): # 对输出的元素进行逐个遍历
for f in range(F):
for j in range(H_out):
for k in range(W_out):
window = x_pad[i, :, j * stride: HH + j * stride, k * stride: WW + k * stride] # 取出涉及的X区域
db[f] += dout[i, f, j, k] # db的结果就是dout
dw[f] += window * dout[i, f, j, k] # dw = x_i * dout
# dx_i = dw * dout
dx_pad[i, :, j * stride:HH + j * stride, k * stride: WW + k * stride] += w[f] * dout[i, f, j, k]
dx = dx_pad[:, :, pad: -pad, pad: -pad] # 截取Max-Pooling 池化层
池化层本质上就是对图像做降采样. 我们或许之前常常听到的是图像2*2降采样分辨率, 但实际上, 最通用的池化层是类似于前面的滑动窗口的方式选择最大值, 有窗口大小和步长. 因此, 我们也就很容易类似于前面的卷积得到公式: (作业有给出)
H\' = 1 + (H - pool_height) / stride # 准确来说还是整除
W\' = 1 + (W - pool_width) / stride所以结果也就得出(注意要善用切片,不要写四层循环了):
N, C, H, W = x.shape
pool_height, pool_width, stride = pool_param[\'pool_height\'], pool_param[\'pool_width\'], pool_param[\'stride\'] # 读取参数
H_out = 1 + (H - pool_height) // stride
W_out = 1 + (W - pool_width) // stride
out = np.zeros((N, C, H_out, W_out))
for j in range(H_out): # 对每个像素
for k in range(W_out):
out[:, :, j, k] = np.max(x[:, :, j * stride:pool_height + j * stride, k * stride: pool_width + k * stride],
axis=(2, 3)) # 取axis2,3最大值反向推导, 因为池化层选取得是最大得那个元素, 所以梯度就和那个元素有关. 我们要做的, 就是得到池化层对应的那个最大是何元素, 然后对它的dx[...] += dout[...].
x, pool_param = cache
N, C, H, W = x.shape
pool_height, pool_width, stride = pool_param[\'pool_height\'], pool_param[\'pool_width\'], pool_param[\'stride\']
H_out = 1 + (H - pool_height) // stride
W_out = 1 + (W - pool_width) // stride
dx = np.zeros_like(x)
for i in range(H_out): # 逐个像素
for j in range(W_out):
x_masked = x[:, :, i * stride:i * stride + pool_width, j * stride:j * stride + pool_height] # 获取原始切片区域
max_x_masked = np.max(x_masked, axis=(2, 3))[:, :, None, None] #得到的最大的结果,None相当于将维度扩大了以便于加回去
# 反馈到原本的位置去. shape从(a,b) => (a,b,1,1) 可以利用广播机制
outmask = (x_masked == max_x_masked)
dx[:, :, i * stride:i * stride + pool_height, j * stride:j * stride + pool_width] += outmask * dout[:,:,i,j][:,:,None,None]
pass快速求解算法初探
虽然题目没有要求做到, 但还是看了一眼.其有一个大致思想, 即: 我们将卷积核变成一个向量, 输入数据变成矩阵(注意为了方便矩阵乘法产生了大量冗余), 随后矩阵乘法(还是那句话,内积可以通过恰当的方式变成矩阵乘法!)之后输出一个向量, reshape之后得到了标准输出. 我还是按照传统艺能给你解释一下, 你应该就明白了(这个解释被极度简化了)

那问题来了, W很好解释, X怎么办呢? 怎么得到这个大矩阵? 这就是np.lib.stride_tricks.as_strided这个函数所做的事了. 关于这个函数的技巧请参考numpy as_strided 入门教程(啰嗦版) - 知乎 (zhihu.com).
def conv_forward_strides(x, w, b, conv_param):
N, C, H, W = x.shape
F, _, HH, WW = w.shape
stride, pad = conv_param[\'stride\'], conv_param[\'pad\']
p = pad
x_padded = np.pad(x, ((0, 0), (0, 0), (p, p), (p, p)), mode=\'constant\') # 补0
H += 2 * pad
W += 2 * pad
out_h = (H - HH) // stride + 1
out_w = (W - WW) // stride + 1 # 到这里为止都还不难
# ---- 反人类预警 ----
shape = (C, HH, WW, N, out_h, out_w) # 首先我们初步确认规模
strides = (H * W, W, 1, C * H * W, stride * W, stride)
strides = x.itemsize * np.array(strides)
x_stride = np.lib.stride_tricks.as_strided(x_padded, # 这里的reshape有点特殊,它可以自由切片reshape同时冗余分配,具体请搜搜这个函数
shape=shape, strides=strides)
x_cols = np.ascontiguousarray(x_stride) # 数据连续存放
x_cols.shape = (C * HH * WW, N * out_h * out_w) # reshape => X大矩阵的目标维度
res = w.reshape(F, -1).dot(x_cols) + b.reshape(-1, 1)
res.shape = (F, N, out_h, out_w)
out = res.transpose(1, 0, 2, 3) # 结果reshape
out = np.ascontiguousarray(out)
cache = (x, w, b, conv_param, x_cols)
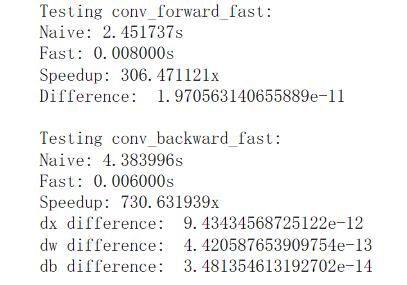
return out, cache这个确实很棒, 避免了对但是实际采用的却不是这种方法, 而是直接写循环, 啊这...

不过这个代码却不完全是python, 而是cython. 利用cython这个工具, 可以在python内调用C底层. 这个代码虽然是python风格的, 但是最终生成的却是c语言代码, 复杂度没有变化, 但是加速效果显著! 有关这个后续我可能会研究, 又要挖坑了...
sandwich层
这个也是题目已经实现好的, 就是直接凑出来,调用就行了. 我们实际上的操作就是 卷积 => 激活函数 => 池化.
a, conv_cache = conv_forward_fast(x, w, b, conv_param)
s, relu_cache = relu_forward(a)
out, pool_cache = max_pool_forward_fast(s, pool_param)
cache = (conv_cache, relu_cache, pool_cache)
return out, cache三层卷积神经网络
我们想要复现的网络结构如下:
conv - relu - 2x2 max pool - affine - relu - affine - softmax这个网络为一层卷积层和两层全连接层构成. 和前面构造两层神经网络一样, 写出代码:
# 初始化
C,H,W = input_dim[0],input_dim[1],input_dim[2]
self.params[\'W1\'] = weight_scale * np.random.randn(num_filters,C,filter_size,filter_size) # 正方形卷积核
self.params[\'b1\'] = np.zeros(num_filters)
# 全连接层,因为这里步长没有自己选择的余地, 根据默认参数,生成图像和输入图像维度一致,pool之后就是H/2*W/2
self.params[\'W2\'] = weight_scale * np.random.randn(num_filters*int(H/2)*int(W/2),hidden_dim)
self.params[\'b2\'] = np.zeros(hidden_dim)
self.params[\'W3\'] = weight_scale * np.random.randn(hidden_dim,num_classes)
self.params[\'b3\'] = np.zeros(num_classes)
pass # 代码块1:前向推导
out_conv, cache_conv = conv_relu_pool_forward(X, W1, b1, conv_param, pool_param)
out_fc1, cache_fc1 = affine_relu_forward(out_conv, W2, b2)
scores, cache_fc2 = affine_forward(out_fc1, W3, b3)
#代码块2: loss & 反向推演
loss, dout = softmax_loss(scores, y)
loss += 0.5 * self.reg * (np.sum(W1 ** 2) + np.sum(W2 ** 2) + np.sum(W3 ** 2)) # 别忘记正则化
dx3, dW3, db3 = affine_backward(dout, cache_fc2)
dx2, dW2, db2 = affine_relu_backward(dx3, cache_fc1)
dx1, dw1, db1 = conv_relu_pool_backward(dx2, cache_conv)
grads[\'W3\'] = dW3 + self.reg * W3
grads[\'b3\'] = db3
grads[\'W2\'] = dW2 + self.reg * W2
grads[\'b2\'] = db2
grads[\'W1\'] = dw1 + self.reg * W1
grads[\'b1\'] = db1随后为了验证正确性,仍然采取很小的数据集, 希望在训练集得到过拟合, 测试集的效果较差.
验证完毕之后就开始正式训练网络. 我们就此感受到了训练时间明显被拉长了, 这里仅仅训练了1个epoch, 在我的电脑上就花费了大约三分钟, 而之前的网络这个时间就可以跑至少50个epoch. 由此我们看出算力对于卷积网络(尤其是深度网络)的意义, 因为矩阵对GPU的天然优势, 后面我们就会转移阵地.但是效果确实不错, 仅仅1个epoch就达到了训练集50.4%,测试集49.9%的准确率了.
可视化的卷积核中, 看出其更加重视局部的特征匹配.

Spatial Batch Normalization
怎么将归一化用在卷积网络呢? 这里大概做法是: 对每个通道内部做正则化. 譬如我们的图片(或者上层输入)为N*C*H*W, 那我们对C个N*H*W内部去做正则化. 实际操作中, 我们希望直接用我们前面的成果而非再写一次, 就应当把图片化成矩阵的形式, 又因为batch norm是列向量的正则化, 所以生成矩阵应当是N*H*W,C的shape.
N, C, H, W = x.shape
x_new = x.transpose(0, 2, 3, 1).reshape(N * H * W, C) # (N,C,H,W) => (N,H,W,C) => (N*H*W,C)
out, cache = batchnorm_forward(x_new, gamma, beta, bn_param) # 直接调用函数.这里cache用原来的目的: 反向也能用之前的backward函数
out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2) # 变成原样backward的代码如下:
N, C, H, W = dout.shape
dout_new = dout.transpose(0, 2, 3, 1).reshape(N * H * W, C)
dx, dgamma, dbeta = batchnorm_backward_alt(dout_new, cache)
dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2) # 直接对dout做reshape即可Group Normalization
还记得我们曾在正则化的博客中提到, layer normalization需谨慎应用于CNN, 因为这么做会导致各个神经元之间的独特特征被抹平. 让我们设想一下, 原本的layer是行向量,也就是对C个通道内部正则化. 因为N*H*W之间没有关联, 那你想想这个图像不得乱套了. 这个方法就是从layer normalization所演化而来的. 这个部分在较早前版本的作业是没有的, 因为是2018年才发表的...

这个的做法是: 我们就缩小正则化的范围, 原本正则化的向量长度仅为C, 而现在被提高到了(C//G)*H*W, 向量数量为N*G, 也就是正则化的对象就是每张图片通道划分成数份去做,而不是武断地直接把所有图像全正则化了.
因为是比较近的论文, 所以直接就给出了gn的tensorflow实现方式...

所以代码自然就清楚了
N, C, H, W = x.shape
# 将特征通道数分组,按照分组重新设置形状
x_group = x.reshape((N, G, C // G, H, W))
mean = np.mean(x_group, axis=(2, 3, 4), keepdims=True)
var = np.var(x_group, axis=(2, 3, 4), keepdims=True)
x_norm = (x_group - mean) / np.sqrt(var + eps) # 归一化
x_norm = x_norm.reshape((N, C, H, W)) # 还原维度
out = x_norm * gamma + beta
cache = (x, gamma, beta, G, eps, mean, var, x_norm)可惜的是, 论文未给出backward地步骤. 我们回顾一下最开始实现的源码:
(x, mean, var, x_hat, eps, gamma, beta) = cache
N = x.shape[0]
dbeta = np.sum(dout, axis=0)
dgamma = np.sum(dout * x_hat, axis=0)
dx_hat = gamma * dout
dvar = np.sum((x - mean) * dx_hat, axis=0) * (-0.5 / np.sqrt(var + eps) ** 3)
# 注意: sum的位置无关紧要,比如把-0.5 / np.sqrt(var + eps) ** 3)包含进sum不影响结果
dmean = -1 / np.sqrt(var + eps) * np.sum(dx_hat, axis=0) + dvar * np.sum(-2 * (x - mean), axis=0) / N
# final gradient
dx = 1 / np.sqrt(var + eps) * dx_hat + 1 / N * dmean + dvar * 2 * (x - mean) / N当时, 从batch => layer只需要把axis变一下就行了. 现在, 我们从简单的gamma开始. 已经知道了规模:
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)dbeta就是广播,反向对应求和,而dgamma是内积求和. 我们延续前面, 但考虑到规模问题, 所以axis=0应当变成axis=0,2,3.
dbeta = np.sum(dout, axis=(0, 2, 3), keepdims=True)
dgamma = np.sum(dout * x_norm, axis=(0, 2, 3), keepdims=True)
dx_hat = dout * gamma后面怎么办? 我们还记得, mean和var是(N,G), 所以为了方便操作广播机制, 我们将得到的dhat转化成原本的格式, 随后一项一项求. 因为我们正则化是2,3,4,keepdim=True, 那现在就也是如此.
dx_hat_ = dx_hat.reshape((N, G, C // G, H, W))
x_ = x.reshape((N, G, C // G, H, W)) # 将x和dxhat均reshape
# 带入公式
dvar = np.sum(dx_hat_ * (x_ - mean), axis=(2, 3, 4), keepdims=True) * -1.0 / 2 / np.sqrt(var + eps) ** (3)
N_GROUP = C // G * H * W
dmean = -1.0 / np.sqrt(var + eps) * np.sum(dx_hat_ , axis=(2, 3, 4), keepdims=True) \\
+ dvar * -2.0 / N_GROUP * np.sum(x_ - mean, axis=(2, 3, 4), keepdims=True)
dx_ = dx_hat_ * 1.0 / np.sqrt(var + eps) \\
+ dmean * 1.0 / N_GROUP \\
+ dvar * 2.0 / N_GROUP * (x_ - mean)
dx = dx_.reshape((N, C, H, W))-- おわり --
2019-CS224n-Assignment2
这次复习cs224n主要是先熟悉python和pytorch,方便之后进行论文复现等工作,同时也回顾一下模型和数学公式推导,找找感觉。
解答:理解词向量(23分)
我们先快速回顾一下word2vec算法,它的核心思想是“一个词的含义取决于它周围的词”。具体来说,我们有一个中心词(center word) c,和这个词 c 周围上下文构成的窗口,这个窗口内的除了 c 之外的词叫做外围词(outside words)。比如下图中,中心词是“banking”,窗口大小为2,所以上下文窗口是:“turning”、”into“、”crises“和”as“。

Skip-gram模型(word2vec的一种实现)目的是习得概率分布 $ P(O|C) $。这样一来,就能计算给定的一个词 o 和词 c 的概率 $ P(O=o|C=c) $(意为,在已知词 c 出现的情况下,词 o 出现的概率), c 是中心词,o 是外围词。
在word2vec中,这个条件概率分布是通过计算向量点积(dot-products),再应用naive-softmax函数得到的:

这里, u o u_o uo 向量代表外围词, v c v_c vc 向量代表中心词。为了包含这些向量,我们有两个矩阵 U \\boldsymbolU U 和 V \\boldsymbolV V 。 U \\boldsymbolU U 的列是外围词, V \\boldsymbolV V 的列是中心词,这两矩阵都有所有词 $w \\in Vocabulary $ 的表示 。
对于词 c 和词 o,损失函数为对数几率:

可以从交叉熵的角度看这个损失函数。真实值为 y \\boldsymboly y ,是一个独热向量,预测值 y ^ \\boldsymbol\\haty y^ 是由公式(1)计算得到。具体来说, y \\boldsymboly y 如果是第k个单词,那么它的第k维为1,其余维都是0,而 y ^ \\boldsymbol\\haty y^ 的第k维表示这是第k个词的概率大小。
问题(a) (3分)
证明公式(2)给出的naive-softmax的损失函数,和 y \\boldsymboly y 与 y ^ \\boldsymbol\\haty y^ 的交叉熵损失函数是一样的,均如下所示(答案控制在一行)

答:
因为除了 o o o 之外的词都不在窗口内,所以只有词 o o o 对损失函数有贡献
问题(b) (5分)
计算损失函数 J n a i v e − s o f t m a x ( v c , o , U ) \\boldsymbolJ_naive-softmax(v_c, o, \\boldsymbolU) Jnaive−softmax(vc,o,U) 对中心词 v c v_c vc 的偏导数,用 y \\boldsymboly y , y ^ \\boldsymbol\\haty y^ 和 U \\boldsymbolU U 来表示。
答:
为了方便表述,对于该外围词 o o o 我们设:
$ x_o = u_o^T v_c , , ,t_o =exp(x_o) , , ,s_o=\\sum_w \\in Vocab exp(x_w)$ , y o ^ = g o = t o s o \\haty_o = g _o=\\fract_os_o yo^=go=soto ,下面对 x o x_o xo 求导
∴ J = − l o g ( y o ^ ) = − l n ( g o ) J = -log(\\haty_o)=-ln(g_o) J=−log(yo^)=−ln(go) (这里的log蕴含意思是ln)
∵ t o ′ = t o = e x o t_o'= t_o = e^x_o to′=to=exo, s ′ = e x o s' = e^x_o s′=exo
∵ g o ′ = t o ′ s o − t o s o ′ s o 2 = g o ( 1 − g o ) g_o' =\\fract_o's_o -t_os'_os_o^2 = g_o (1-g_o) go′=so2to′so−toso′=go(1−go)
∴ $\\frac\\partialJ\\partialx_o = \\frac\\partialJ\\partialg_o · \\frac\\partialg_o\\partialx_o = \\haty_o - y_o $
则对 v c v_c vc 的导数为:
∂ J ∂ v c = ∂ J ∂ x o ⋅ ∂ x o ∂ v c = ( y o ^ − y o ) ⋅ u T \\frac\\partialJ\\partialv_c=\\frac\\partialJ\\partialx_o · \\frac\\partialx_o\\partialv_c = (\\haty_o - y_o) · u^T ∂vc∂J=∂xo∂J⋅∂vc∂xo=(yo^−yo)⋅uT,引入矩阵得:
$\\boldsymbolJ_native-softmax=(v_c, o, \\boldsymbolU) = (\\haty - y) · \\boldsymbolU $
问题© (5分)
计算损失函数 J n a i v e − s o f t m a x ( v c , o , U ) \\boldsymbolJ_naive-softmax(v_c, o, \\boldsymbolU) Jnaive−softmax(vc,o,U) 对上下文窗口内的词 w w w 的偏导数,考虑两种情况,即 w 是外围词 o o o,和 w 不是 o o o,用 y \\boldsymboly y , y ^ \\boldsymbol\\haty y^ 和 v c v_c vc 来表示。
答:
在问题(b)基础上,对 x w = u w T v c x_w=u_w^Tv_c xw=u