JAVA 用 List 实现堆
Posted lalala
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了JAVA 用 List 实现堆相关的知识,希望对你有一定的参考价值。
大顶堆:每个父节点都大于子节点
小顶堆:每个父节点都小于子节点
在堆中,每次加入元素或者移除元素,都要调整堆的位置,使其满足堆的定义。
常用于 topK 问题,k 个最大/最小元素,每次弹出大顶堆/小顶堆 堆顶元素即可。
以及堆排序问题,堆排序可以看成是将待排序的数组元素依次加入堆(每次加入都调整堆)构建一个初始大顶/小顶堆。再依次弹出堆顶元素(每次弹出都调整堆)。
堆是用完全二叉树实现的,而完全二叉树可以用数组来表示。
1. 若array[0,...,n-1]表示一颗完全二叉树的顺序存储模式,则双亲节点指针和孩子结点指针之间的内在关系如下:
任意一节点指针 i:父节点:i==0 ? null : (i-1)/2
左孩子:2*i + 1
右孩子:2*i + 2
2. 堆的定义:n个关键字序列array[0,...,n-1],当且仅当满足下列要求:(0 <= i <= (n-1)/2)
① array[i] <= array[2*i + 1] 且 array[i] <= array[2*i + 2]; 称为小根堆;
② array[i] >= array[2*i + 1] 且 array[i] >= array[2*i + 2]; 称为大根堆;
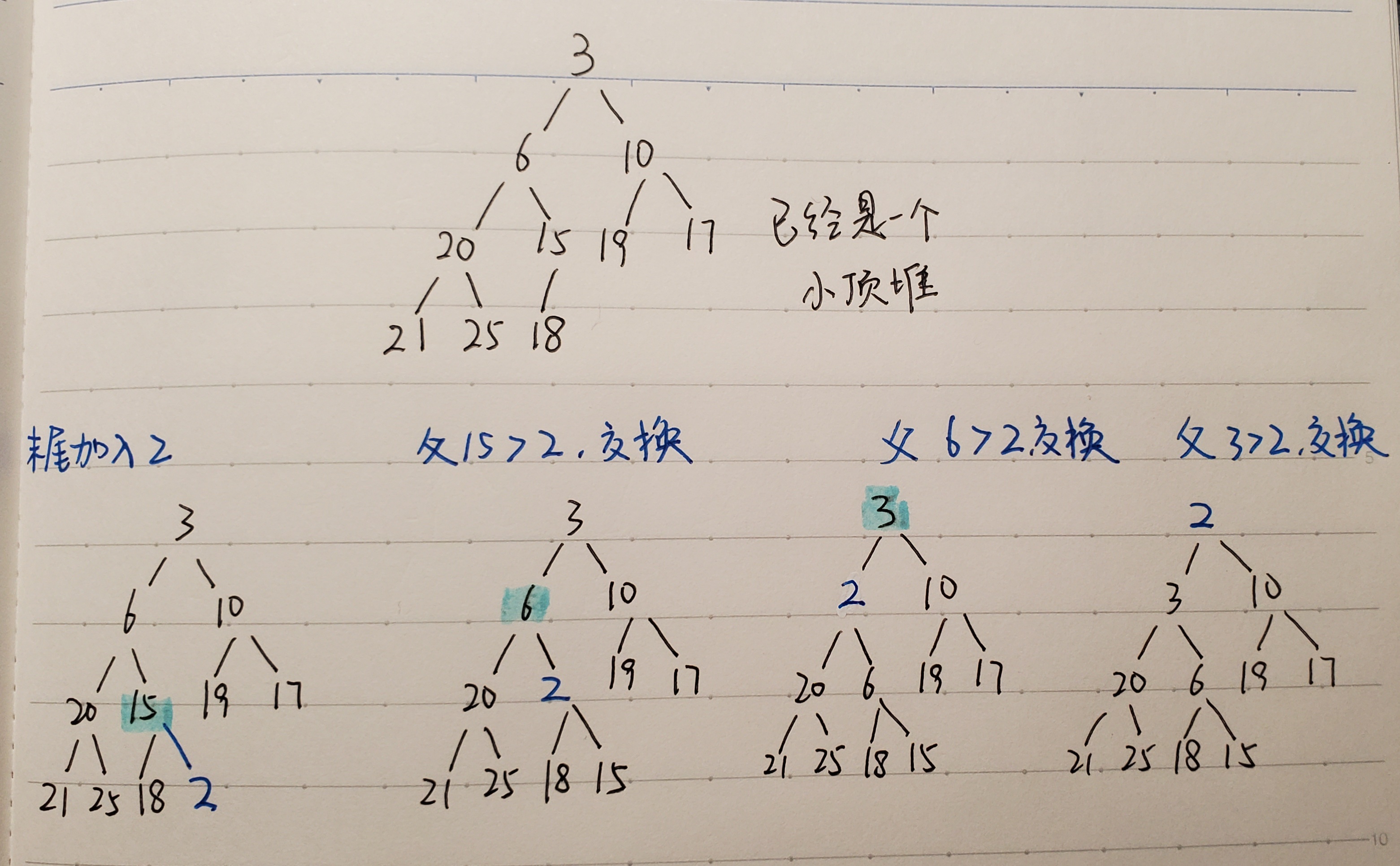
以下以小顶堆为例,说明两个基本问题
1、如何将元素加入堆?
前情:每次加入元素,都会调整堆,使其符合堆的定义。所以每次元素加入的一定是一个符合定义的堆。
每次将元素加入堆的末尾,从末尾逐步将这个元素调整到合适的位置。
每次调整都至少应该使得 【要调整的这个元素(新加入堆末尾)、其父节点、其兄弟节点】 三者满足小顶堆的定义:父节点比两个孩子节点都小
由于我们强调过前提是 元素加入的一定是一个符合定义的堆,所以 其父节点和其兄弟节点 一定满足堆的定义,即父节点一定比兄弟节点小
所以我们只需保证一个:就是其父节点比这个新加入的元素小,如果不满足,就要交换父节点和这个节点
交换后,这个元素的新位置、新的父节点、新的兄弟节点 三者可能仍然不满足小顶堆的定义,继续与新的父节点比较,进行调整
........
直到这个元素上浮到一个符合定义的位置:父节点比自己和兄弟节点都小,就完成了堆的调整。
/* 先加入到底部最后一个,再从下往上上升,每当判断父节点比自己大(小顶堆)则交换 */ public void offer(Integer e) // 先加入到底部,最后一个 list.add(e); if (list.isEmpty()) return; int thisIndex = list.size() - 1; int parentIndex = (thisIndex - 1) /2; // 每次都 offer 的 话,那么现在肯定是一个小顶堆,父节点比已有的左节点(有可能没有左节点)小 // 【所以先不用关注左节点,只关注父节点】 // 一直从底向上调整到父节点比自己小 while (parentIndex >= 0 && list.get(parentIndex) > list.get(thisIndex)) //小顶堆,如果父节点大于当前节点,则交换位置 swapListE(list, parentIndex, thisIndex); // 现在这个节点下标等于之前父节点的 thisIndex = parentIndex; // 新的父节点下标 parentIndex = (thisIndex - 1) /2; // 获取小顶堆顶端的元素 public Integer peek() if (list.isEmpty()) return null; return list.get(0);
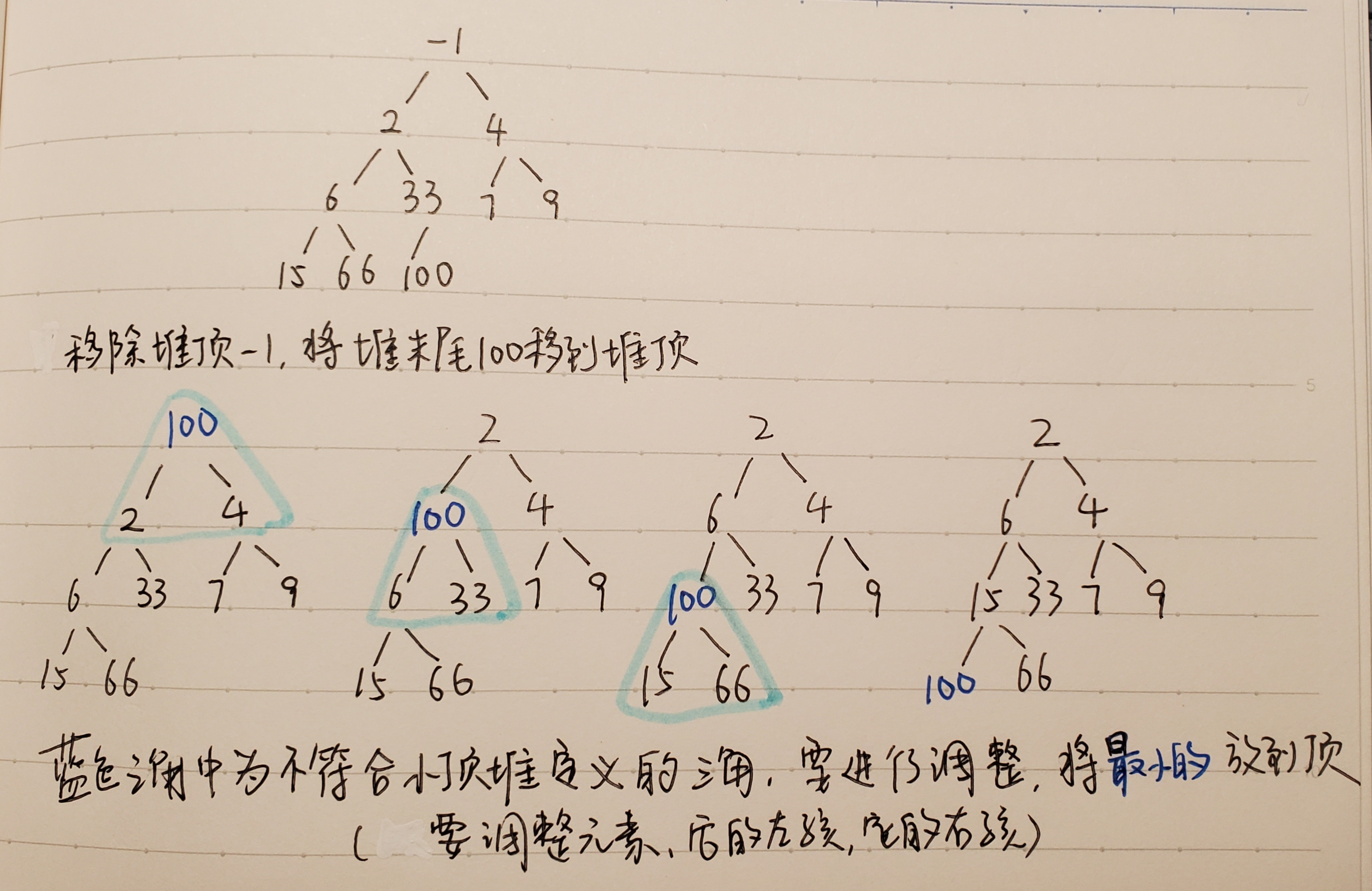
2、如何移除堆顶元素?
将堆顶元素移除,并将堆末尾元素放到堆顶,再调整堆,使新的堆顶到它合适的位置
同样,要使得至少 【要调整的这个元素(从堆末尾到堆顶的),它的左孩子,它的右孩子】 三者符合小顶堆的定义,这个元素要比它的左右孩子都小。如果不符合,就要进行调整
调整时,简单说就是将三者中最小的放到顶。细分有以下几种情况
1、当前元素没有左右孩子:符合堆的定义,不用调整
2、当前元素只有一个左孩子(完全二叉树不可能只有右孩子):比左孩子小,则符合堆的定义,不用调整;比左孩子大,则与左孩子进行交换
3、当前元素有左、右两个孩子:
a.比左右两孩子都小,符合堆的定义,不用调整
b.处于两个孩子中间,则与比自己小的那个交换
c.比两个孩子都大,则与两个孩子中较小的那个进行交换
交换后,这个元素的新位置、新的左孩子、新的右孩子 三者可能仍然不满足小顶堆的定义,继续与新的左右孩子比较,进行调整
........
直到这个元素下沉到一个符合定义的位置:父节点比自己和兄弟节点都小,就完成了堆的调整。
/* 弹出顶端,再把底部最后拉到最顶端,在从上往下依次下沉,每当判断孩子节点比自己小(小顶堆) */ public Integer poll() if (list.isEmpty()) return null; // 暂存顶部元素 Integer topE = list.get(0); if (list.size() == 1) list.remove(0); return topE; // 将底部元素交换到顶部 swapListE(list, 0, list.size() - 1); // 移除要弹出的曾经的顶部元素 list.remove(list.size() - 1); /* 要使得至少 【要调整的这个元素(从堆末尾到堆顶的),它的左孩子,它的右孩子】 三者符合小顶堆的定义 如果符合定义,则返回 -1 ,如果不符合定义,则返回要交换的那个元素的下标 */ int thisIndex = 0;int needSwapChirldrenIndex = getNeedSwapChirldrenIndex(list, thisIndex); while(needSwapChirldrenIndex != -1) swapListE(list, thisIndex, needSwapChirldrenIndex); thisIndex = needSwapChirldrenIndex; needSwapChirldrenIndex = getNeedSwapChirldrenIndex(list, thisIndex); return topE; /* 判断根节点和它的左右孩子是否满足小顶堆,满足则返回 -1,不满足则返回要交换的那个元素的下标,几种情况 1、当前元素没有左右孩子:不用交换,返回 -1 1、当前元素只有左孩子:比左孩子小不用交换返回-1;比左孩子大与左孩子交换,返回左孩 index 2、当前元素有左右两个孩子 a、比左右孩子都小,不用交换,返回 -1 b、处于两孩子中间,则与比自己小的那个交换 c、比两个孩子都大,则与两个孩子中较小的那个交换 */ // 该方法判断根节点和它的左右孩子是否满足小顶堆,满足则返回 -1,不满足则返回要交换的那个元素的下标 private int getNeedSwapChirldrenIndex(List<Integer> list, int rootIndex) Integer rootValue = list.get(rootIndex); int leftIndex = 2*rootIndex + 1; int rightIndex = 2*rootIndex + 2; Integer leftValue = null; Integer rightValue = null; if (leftIndex > 0 && leftIndex < list.size()) leftValue = list.get(leftIndex); if (rightIndex > 0 && rightIndex < list.size()) rightValue = list.get(rightIndex); // 返回 -1 , 表示符合大顶堆 // 左右孩子都没有,符合 if (leftValue == null && rightValue == null) return -1; // 只有左孩子 else if (rightValue == null) if (rootValue > leftValue) // 不符合,返回左孩子的下标,要与左孩子交换 return leftIndex; else // 符合,返回 -1 return -1; // 完全二叉树,没有 只有右孩子 的情况 else if (leftValue == null) return -1; // 左右孩子都有 else // 比两个孩子都小,不用交换 if (rootValue < leftValue && rootValue < rightValue) return -1; // 小于左孩子,大于右孩子。与右孩子交换 else if (rootValue < leftValue && rootValue > rightValue) return rightIndex; // 小于右孩子,大于左孩子。与左孩子交换 else if (rootValue < rightValue && rootValue > leftValue) return leftIndex; // 比左右孩子都大 else if (rootValue > rightValue && rootValue > leftValue) // 与两个孩子中较小的那个交换 if (leftValue < rightValue) return leftIndex; else return rightIndex; else return -1;
3、堆排序
可以看成是将待排序的数组元素依次加入堆(每次加入都调整堆)构建一个初始大顶/小顶堆。再依次弹出堆顶元素(每次弹出都调整堆),每次弹出最大/最小,相当于完成了排序。
private static void heapOrder(int[] arr) Heap heap = new Heap(); for (int e : arr) heap.offer(e); for (int i=0;i<arr.length;i++) arr[i] = heap.poll();
4、Java 优先级队列的用法
待补充
java数据结构----堆
1.堆:堆是一种树,由它实现的优先级队列的插入和删除的时间复杂度都是O(logn),用堆实现的优先级队列虽然和数组实现相比较删除慢了些,但插入的时间快的多了。当速度很重要且有很多插入操作时,可以选择堆来实现优先级队列。
2.java的堆和数据结构堆:java的堆是程序员用new能得到的计算机内存的可用部分。而数据结构的堆是一种特殊的二叉树。
3.堆是具有如下特点的二叉树:
3.1.它是完全二叉树,也就是说除了树的最后一层节点不需要是满的,其他的每一层从左到右都必须是满的。
3.1.1.完全二叉树图解: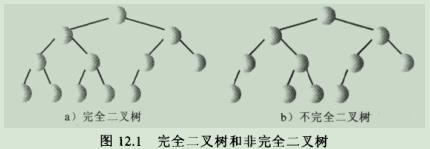
3.2.它常常用数组实现。
3.2.1.数组和堆的对应关系示意图:
3.3.堆中每一个节点都满足堆的条件,也就是说每一个关键字的值都大于或等于这个节点的子节点的关键字值。
堆是完全二叉树的事实说明了表示堆的数组中没有空项,即从0-->n-1的每个数据单元都有数据项。
4.堆在存储器中的表示是数组,堆只是一个概念上的表示。
5.堆的弱序:堆和二叉搜索树相比是弱序的,在二叉搜索树中,当前节点的值总是比左子节点的值大,却比它的右子节点的值小,因此按序遍历相对容易。而堆的组织规则弱,它只要求从根到叶子节点的每一条路径,节点都是按降序排列的。同一节点的左右子节点都没有规律。因此,堆不支持按序遍历,也不能在堆上便利的查找指定关键字,因为在查找的过程中,没有足够的信息决定选择通过节点的两个那一个走向下一层。它也不能在少于O(logn)的时间内删除一个指定的节点,因为没有办法找到这个节点。因此,堆的这种近乎无序的规则似乎毫无用处,不过对于快速移除最大节点的操作,以及快速插入新节点的操作,这种顺序已经足够了。这些操作是使用堆作为优先级队列所需要的全部操作。
6.移除操作:移除是指删掉关键字值最大的节点,即根节点。移除思路如下:
6.1.移走根,
6.2.把左后一个节点移到根的位置,
6.3.一直向下筛选这个节点,知道它在一个大于它的节点之下,小于它的节点之上为止。
6.4.过程图解: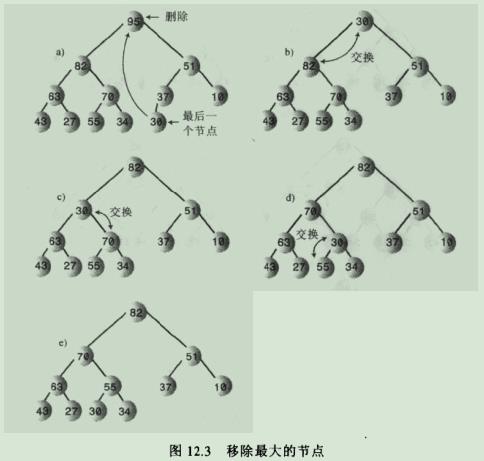
说明:在被筛选节点的每个暂时停留的位置,向下筛选的算法总是要检查那一个子节点更大,然后目标节点和较大的子节点交换位置,如果要把目标节点和较小的子节点交换,那么这个子节点就会变成大子节点的父节点,这就违背了堆的条件。
7.堆的插入:插入使用向上筛选,节点最后插入到数组最后第一个空着的单元中,数组容量大小增加1。
7.1.插入图解: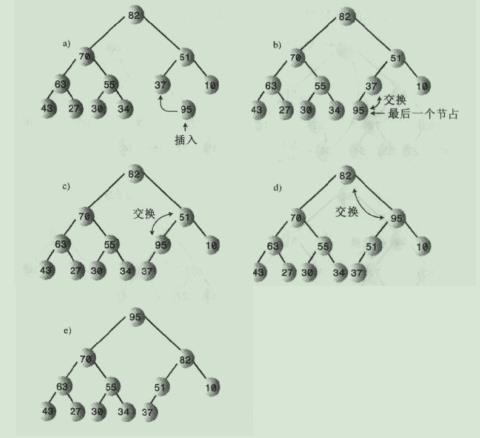
说明:向上筛选的算法比向下筛选的算法相对简单,因为它不需要比较两个子节点关键字值的大小,节点只有一个父节点。目标节点主要和它的父亲节点换位即可。
7.2.不是真的交换: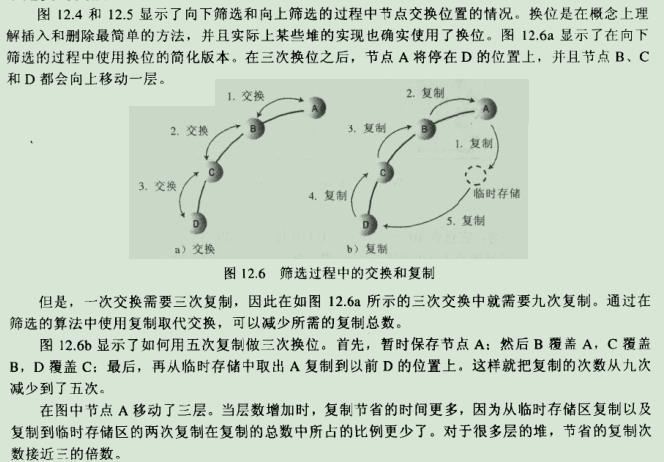
8.用数组表示一棵树时,如果数组中节点的索引位x,则
a.它的父节点的下标是:(x-1)/2;
b.它的左子节点的下标为2*x + 1;
c.它的右子节点的下标是2*x + 2;
9.堆的代码:
9.1.Node.java

1 package com.cn.heap; 2 /** 3 * 堆的节点类 4 * @author Administrator 5 * 6 */ 7 public class Node { 8 private int iData; 9 public Node(int id){ 10 iData = id; 11 } 12 public int getkey(){ 13 return iData; 14 } 15 public void setkey(int id){ 16 iData = id; 17 } 18 }
9.2.Heap.java

1 package com.cn.heap; 2 /** 3 * 堆的实现类 4 * @author Administrator 5 * 6 */ 7 public class Heap { 8 private Node[] heapArray; 9 private int maxSize; 10 private int currentSize; 11 public Heap(int mx){ 12 maxSize = mx; 13 heapArray = new Node[maxSize]; 14 currentSize = 0; 15 } 16 public boolean isEmpty(){ 17 return currentSize == 0 ; 18 } 19 public boolean insert(int key){ 20 if (currentSize == maxSize) 21 return false; 22 Node thenode = new Node(key); 23 heapArray[currentSize] = thenode; 24 trickleUp(currentSize ++); 25 return true; 26 } 27 public void trickleUp(int index){ 28 int parent = (index - 1) / 2; 29 Node bottom = heapArray[index]; 30 while (index > 0 && heapArray[parent].getkey() < bottom.getkey()){ 31 heapArray[index] = heapArray[parent]; 32 index = parent; 33 parent = (parent - 1) / 2; 34 } 35 heapArray[index] = bottom; 36 } 37 public Node remove(){ 38 Node root = heapArray[0]; 39 heapArray[0] = heapArray[-- currentSize]; 40 trickleDown(0); 41 return root; 42 } 43 public void trickleDown(int index){ 44 int largeChild; 45 Node top = heapArray[index]; 46 while (index < currentSize / 2){ 47 int leftChild = 2 * index + 1; 48 int rightChild = 2 * index + 2; 49 if (rightChild < currentSize && heapArray[leftChild].getkey() < heapArray[rightChild].getkey()) 50 largeChild = rightChild; 51 else 52 largeChild = leftChild; 53 if (top.getkey() >= heapArray[largeChild].getkey()) 54 break; 55 heapArray[index] = heapArray[largeChild]; 56 index = largeChild; 57 } 58 heapArray[index] = top; 59 } 60 public boolean change(int index,int newvalue){ 61 if (index < 0 || index >=currentSize) 62 return false; 63 int oldvalue = heapArray[index].getkey(); 64 heapArray[index].setkey(newvalue); 65 if (oldvalue < newvalue) 66 trickleUp(index); 67 else 68 trickleDown(index); 69 return true; 70 } 71 public void displayHeap(){ 72 System.out.print("heapArray:"); 73 for (int i = 0; i < currentSize; i++) { 74 if (heapArray[i] != null) 75 System.out.print(heapArray[i].getkey()+" "); 76 else 77 System.out.print("--"); 78 } 79 System.out.println(""); 80 int nBlanks = 32; 81 int itemsPerrow = 1; 82 int column = 0; 83 int j = 0; 84 String dots = "........................"; 85 System.out.println(dots + dots); 86 while (currentSize > 0){ 87 if (column == 0) 88 for (int i = 0; i < nBlanks; i++) { 89 System.out.print(" "); 90 } 91 System.out.print(heapArray[j].getkey()); 92 if (++ j == currentSize) 93 break; 94 if (++ column == itemsPerrow){ 95 nBlanks /= 2; 96 itemsPerrow *= 2; 97 column = 0; 98 System.out.println(); 99 } 100 else 101 for (int i = 0; i < nBlanks * 2 - 2; i++) 102 System.out.print(\' \'); 103 } 104 System.out.println("\\n"+dots + dots); 105 } 106 }
9.3.HTest.java

1 package com.cn.heap; 2 /** 3 * heap类的测试 4 * @author Administrator 5 * 6 */ 7 public class HTest { 8 public static void main(String[] args) { 9 Heap h = new Heap(10); 10 h.insert(10); 11 h.insert(30); 12 h.insert(20); 13 h.insert(18); 14 h.insert(12); 15 h.displayHeap(); 16 h.remove(); 17 h.displayHeap(); 18 } 19 }
10.堆的效率:上述操作的时间复杂度是:O(logn)。
11.堆排序实现思路:使用insert()向堆中插入所有无序的数据项,然后重复使用remove()方法,就可以按序移除所有数据项,它的效率和快速排序类似,都是O(NlogN),但快排稍微快些,因为堆插入时的向下筛选多出的比较所占用的时间。
11.1.Node.java

1 package com.cn.heap; 2 /** 3 * 堆的节点类 4 * @author Administrator 5 * 6 */ 7 public class Node { 8 private int iData; 9 public Node(int id){ 10 iData = id; 11 } 12 public int getkey(){ 13 return iData; 14 } 15 public void setkey(int id){ 16 iData = id; 17 } 18 }
11.2.Heap.java

1 package com.cn.heap; 2 /** 3 * 堆的实现类 4 * @author Administrator 5 * 6 */ 7 public class Heap { 8 private Node[] heapArray; 9 private int maxSize; 10 private int currentSize; 11 public Heap(int mx){ 12 maxSize = mx; 13 heapArray = new Node[maxSize]; 14 currentSize = 0; 15 } 16 public boolean isEmpty(){ 17 return currentSize == 0 ; 18 } 19 public boolean insert(int key){ 20 if (currentSize == maxSize) 21 return false; 22 Node thenode = new Node(key); 23 heapArray[currentSize] = thenode; 24 trickleUp(currentSize ++); 25 return true; 26 } 27 public void trickleUp(int index){ 28 int parent = (index - 1) / 2; 29 Node bottom = heapArray[index]; 30 while (index > 0 && heapArray[parent].getkey() < bottom.getkey()){ 31 heapArray[index] = heapArray[parent]; 32 index = parent; 33 parent = (parent - 1) / 2; 34 } 35 heapArray[index] = bottom; 36 } 37 public Node remove(){ 38 Node root = heapArray[0]; 39 heapArray[0] = heapArray[-- currentSize]; 40 trickleDown(0); 41 return root; 42 } 43 public void trickleDown(int index){ 44 int largeChild; 45 Node top = heapArray[index]; 46 while (index < currentSize / 2){ 47 int leftChild = 2 * index + 1; 48 int rightChild = 2 * index + 2; 49 if (rightChild < currentSize && heapArray[leftChild].getkey() < heapArray[rightChild].getkey()) 50 largeChild = rightChild; 51 else 52 largeChild = leftChild; 53 if (top.getkey() >= heapArray[largeChild].getkey()) 54 break; 55 heapArray[index] = heapArray[largeChild]; 56 index = largeChild; 57 } 58 heapArray[index] = top; 59 } 60 public boolean change(int index,int newvalue){ 61 if (index < 0 || index >=currentSize) 62 return false; 63 int oldvalue = heapArray[index].getkey(); 64 heapArray[index].setkey(newvalue); 65 if (oldvalue < newvalue) 66 trickleUp(index); 67 else 68 trickleDown(index); 69 return true; 70 } 71 public void displayHeap(){ 72 System.out.print("heapArray:"); 73 for (int i = 0; i < currentSize; i++) { 74 if (heapArray[i] != null) 75 System.out.print(heapArray[i].getkey()+" "); 76 else 77 System.out.print("--"); 78 } 79 System.out.println(""); 80 int nBlanks = 32; 81 int itemsPerrow = 1; 82 int column = 0; 83 int j = 0; 84 String dots = "........................"; 85 System.out.println(dots + dots); 86 while (currentSize > 0){ 87 if (column == 0) 88 for (int i = 0; i < nBlanks; i++) { 89 System.out.print(" "); 90 } 91 System.out.print(heapArray[j].getkey()); 92 if (++ j == currentSize) 93 break; 94 if (++ column == itemsPerrow){ 95 nBlanks /= 2; 96 itemsPerrow *= 2; 97 column = 0; 98 System.out.println(); 99 } 100 else 101 for (int i = 0; i < nBlanks * 2 - 2; i++) 102 System.out.print(\' \'); 103 } 104 System.out.println("\\n"+dots + dots); 105 } 106 public void displayArray(){ 107 for (int i = 0; i < maxSize; i++) 108 System.out.print(heapArray[i].getkey()+" "); 109 System.out.println(); 110 } 111 public void insertAt(int index,Node newnode){ 112 heapArray[index] = newnode; 113 } 114 public void incrementSize(){ 115 currentSize ++; 116 } 117 }
11.3.HeapSort.java

1 package com.cn.heap; 2 3 import java.util.Scanner; 4 5 /** 6 * 基于堆的排序----堆排序 7 * @author Administrator 8 * 9 */ 10 public class HeapSort { 11 public static void main(String[] args) { 12 int size,j; 13 Scanner in = new Scanner(System.in); 14 System.out.print("Enter number of items: "); 15 size = in.nextInt(); 16 Heap theheap = new Heap(size); 17 for (int i = 0; i < size; i++) { 18 int random = (int)(Math.random()*100); 19 Node node = new Node(random); 20 theheap.insertAt(i, node); 21 theheap.incrementSize(); 22 } 23 System.out.print("random: "); 24 theheap.displayArray(); 25 for (int i = size / 2 - 1; i >= 0; i --) { 26 theheap.trickleDown(i); 27 } 28 System.out.print("heap: "); 29 theheap.displayArray(); 30 theheap.displayHeap(); 31 for (int i = size - 1; i >= 0; i --) { 32 Node node = theheap.remove(); 33 theheap.insertAt(i,node); 34 } 35 System.out.print("sorted: "); 36 theheap.displayArray(); 37 } 38 }
以上是关于JAVA 用 List 实现堆的主要内容,如果未能解决你的问题,请参考以下文章
