数模预测模型那些

Posted 2023-04-12

01、线性回归
线性回归比较经典的模型之一，英国科学家Francis Galton在19世纪就使用了 "回归 "一词，并且仍然是使用数据表示线性关系最有效的模型之一。线性回归是世界范围内，许多计量经济学课程的主要内容。学习该线性模型将让你在解决回归问题有方向，并了解如何用数学知识来预测现象。

02、逻辑回归
虽然名为回归，但逻辑回归是掌握分类问题的最佳模型。学习逻辑回归有以下几点优势：
初步了解分类和多分类问题，这是机器学习任务的重要部分
理解函数转换，如Sigmoid函数的转换
了解梯度下降的其他函数的用法，以及如何对函数进行优化。
03、决策树
首先要研究的非线性算法应该是决策树。决策树是一种基于if-else规则的，相对简单且可解释的算法，它将让你很好地掌握非线性算法及其优缺点。决策树是所有基于树模型的基础，通过学习决策树，你还将准备学习其他技术，如XGBoost或LightGBM。而且，决策树同时适用于回归和分类问题，两者之间的差异最小，选择影响结果的最佳变量的基本原理大致相同，你只是换了一个标准来做。

04、随机森林
由于决策树对超参数和简单假设的敏感性，决策树的结果相当有限。当你深入了解后，你会明白决策树很容易过度拟合，从而得出的模型对未来缺乏概括性。随机森林的概念非常简单。有助于在不同的决策树之间实现多样化，从而提高算法的稳健性。就像决策树一样，你可以配置大量的超参数，以增强这种集成模型的性能。

参考技术A

数模预测模型具体有：

1、蒙特卡罗算法（该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟可以来检验自己模型的正确性，是比赛时必用的方法）

2、数据拟合、参数估计、插值等数据处理算法（比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具）

3、线性规划、整数规划、多元规划、二次规划等规划类问题（建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现）

4、图论算法（这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备）

5、动态规划、回溯搜索、分治算法、分支定界等计算机算法（这些算法是算法设计中比较常用的方法，很多场合可以用到竞赛中）

6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法（这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用）

7、网格算法和穷举法（网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具）

8、一些连续离散化方法（很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的）

9、数值分析算法（如果在比赛中采用高级语言进行编程的话，那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用）

10、图象处理算法（赛题中有一类问题与图形有关，即使与图形无关，论文中也应该要不乏图片的，这些图形如何展示以及如何处理就是需要解决的问题，通常使用Matlab进行处理）

关于损失函数那些事儿

一、说明

　　非原创，来源：磐创AI公众号 （略有修改）。

二、内容

损失函数（loss function）又叫做代价函数（cost function），是用来评估模型的预测值与真实值不一致的程度，也是神经网络中优化的目标函数，神经网络训练或者优化的过程就是最小化损失函数的过程，损失函数越小，说明模型的预测值就越接近真是值，模型的健壮性也就越好。

常见的损失函数有以下几种：

(1) 0-1损失函数(0-1 lossfunction):

0-1损失函数是最为简单的一种损失函数，多适用于分类问题中，如果预测值与目标值不相等，说明预测错误，输出值为1；如果预测值与目标值相同，说明预测正确，输出为0，言外之意没有损失。其数学公式可表示为：

 

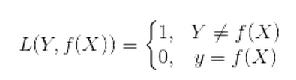
由于0-1损失函数过于理想化、严格化，且数学性质不是很好，难以优化，所以在实际问题中，我们经常会用以下的损失函数进行代替。

（2）感知损失函数（Perceptron Loss）：
感知损失函数是对0-1损失函数的改进，它并不会像0-1损失函数那样严格，哪怕预测值为0.99，真实值为1，都会认为是错误的；而是给一个误差区间，只要在误差区间内，就认为是正确的。其数学公式可表示为：

 

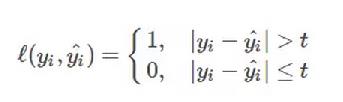
（3）平方损失函数（quadratic loss function）：

顾名思义，平方损失函数是指预测值与真实值差值的平方。损失越大，说明预测值与真实值的差值越大。平方损失函数多用于线性回归任务中，其数学公式为：          

 

接下来，我们延伸到样本个数为N的情况，此时的平方损失函数为：

 

 

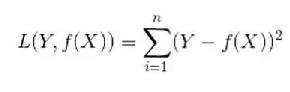
（4）Hinge损失函数（hinge loss function）：

Hinge损失函数通常适用于二分类的场景中，可以用来解决间隔最大化的问题，常应用于著名的SVM算法中。其数学公式为：

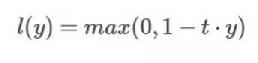
其中在上式中，t是目标值{-1，+1}，y为预测值的输出，取值范围在（-1，1）之间。

更多关于Hinge Loss参考：https://blog.csdn.net/luo123n/article/details/48878759 

 

（5）对数损失函数（Log Loss）：

对数损失函数也是常见的一种损失函数，常用于逻辑回归问题中，其标准形式为：

上式中，y为已知分类的类别，x为样本值，我们需要让概率p(y|x)达到最大值，也就是说我们要求一个参数值，使得输出的目前这组数据的概率值最大。因为概率P(Y|X)的取值范围为[0,1]，log(x)函数在区间[0,1]的取值为负数，所以为了保证损失值为正数要在log函数前加负号。

（6）交叉熵损失函数（cross-entropy loss function）：

交叉熵损失函数本质上也是一种对数损失函数，常用于多分类问题中。其数学公式为：

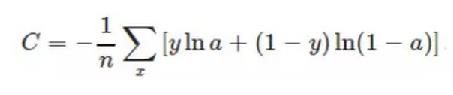
注意：公式中的x表示样本，y代表预测的输出，a为实际输出，n表示样本总数量。交叉熵损失函数常用于当sigmoid函数作为激活函数的情景，因为它可以完美解决平方损失函数权重更新过慢的问题