python5
Posted 林木森3
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python5相关的知识,希望对你有一定的参考价值。
import pandas as pd import matplotlib.pyplot as plt datafile =r"C:\\Users\\Minori\\Desktop\\python实训\\original_data.xls" # 输入的数据文件 data = pd.read_excel(datafile) # 读取数据 # 查看有无水流的分布 # 数据提取 lv_non = pd.value_counts(data[\'有无水流\'])[\'无\'] lv_move = pd.value_counts(data[\'有无水流\'])[\'有\'] # 绘制条形图 fig = plt.figure(figsize = (6 ,5)) # 设置画布大小 plt.rcParams[\'font.sans-serif\'] = \'SimHei\' # 设置中文显示 plt.rcParams[\'axes.unicode_minus\'] = False plt.bar([0,1], height=[lv_non,lv_move], width=0.4, alpha=0.8, color=\'skyblue\') plt.xticks([index for index in range(2)], [\'无\',\'有\']) plt.xlabel(\'水流状态\') plt.ylabel(\'记录数\') plt.title(\'不同水流状态记录数3127\') plt.show() plt.close() # 查看水流量分布 water = data[\'水流量\'] # 绘制水流量分布箱型图 fig = plt.figure(figsize = (5 ,8)) plt.boxplot(water, patch_artist=True, labels = [\'水流量\'], # 设置x轴标题 boxprops = \'facecolor\':\'lightblue\') # 设置填充颜色 plt.title(\'水流量分布箱线图3127\') # 显示y坐标轴的底线 plt.grid(axis=\'y\') plt.show()
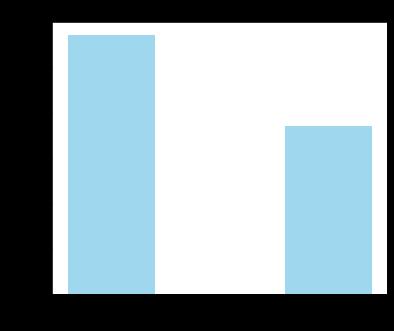
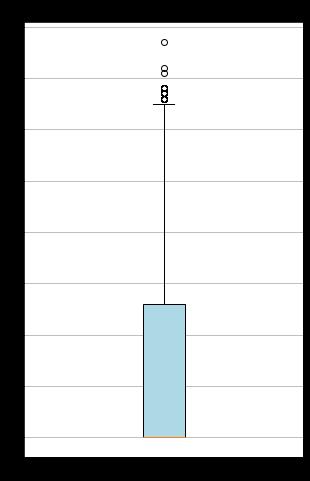
# ´代码10-2 import pandas as pd import numpy as np data = pd.read_excel(\'./original_data.xls\') print(\'初始状态的数据形状为:\', data.shape) # 删除热水器编号、有无水流、节能模式属性 data.drop(labels=["热水器编号","有无水流","节能模式"],axis=1,inplace=True) print(\'删除冗余属性后的数据形状为:\', data.shape) data.to_csv(\'./water_heart.csv\',index=False)

data = pd.read_csv(\'./water_heart.csv\') # 划分用水事件 threshold = pd.Timedelta(\'4 min\') # 阈值为4分钟 data[\'发生时间\'] = pd.to_datetime(data[\'发生时间\'], format = \'%Y%m%d%H%M%S\') # 转换时间格式 data = data[data[\'水流量\'] > 0] # 只要流量大于0的记录 sjKs = data[\'发生时间\'].diff() > threshold # 相邻时间向前差分,比较是否大于阈值 sjKs.iloc[0] = True # 令第一个时间为第一个用水事件的开始事件 sjJs = sjKs.iloc[1:] # 向后差分的结果 sjJs = pd.concat([sjJs,pd.Series(True)]) # 令最后一个时间作为最后一个用水事件的结束时间 # 创建数据框,并定义用水事件序列 sj = pd.DataFrame(np.arange(1,sum(sjKs)+1),columns = ["事件序号"]) sj["事件起始编号"] = data.index[sjKs == 1]+1 # 定义用水事件的起始编号 sj["事件终止编号"] = data.index[sjJs == 1]+1 # 定义用水事件的终止编号 print(\'当阈值为4分钟的时候事件数目为:\',sj.shape[0]) sj.to_csv(\'./sj.csv\',index = False)
结果为:当阈值为4分钟的时候事件数目为: 172
n = 4 # 使用以后四个点的平均斜率 threshold = pd.Timedelta(minutes=5) # 专家阈值 data[\'发生时间\'] = pd.to_datetime(data[\'发生时间\'], format=\'%Y%m%d%H%M%S\') data = data[data[\'水流量\'] > 0] # 只要流量大于0的记录 # 自定义函数:输入划分时间的时间阈值,得到划分的事件数 def event_num(ts): d = data[\'发生时间\'].diff() > ts # 相邻时间作差分,比较是否大于阈值 return d.sum() + 1 # 这样直接返回事件数 dt = [pd.Timedelta(minutes=i) for i in np.arange(1, 9, 0.25)] h = pd.DataFrame(dt, columns=[\'阈值\']) # 转换数据框,定义阈值列 h[\'事件数\'] = h[\'阈值\'].apply(event_num) # 计算每个阈值对应的事件数 h[\'斜率\'] = h[\'事件数\'].diff()/0.25 # 计算每两个相邻点对应的斜率 h[\'斜率指标\']= h[\'斜率\'].abs().rolling(4).mean() # 往前取n个斜率绝对值平均作为斜率指标 ts = h[\'阈值\'][h[\'斜率指标\'].idxmin() - n] # 用idxmin返回最小值的Index,由于rolling_mean()计算的是前n个斜率的绝对值平均 # 所以结果要进行平移(-n) if ts > threshold: ts = pd.Timedelta(minutes=4) print(\'计算出的单次用水时长的阈值为:\',ts)
结果为:计算出的单次用水时长的阈值为: 0 days 00:04:00
data = pd.read_excel(\'.\\water_hearter.xlsx\') # 读取热水器使用数据记录 sj = pd.read_csv(\'./sj.csv\') # 读取用水事件记录 # 转换时间格式 data["发生时间"] = pd.to_datetime(data["发生时间"],format="%Y%m%d%H%M%S") # 构造特征:总用水时长 timeDel = pd.Timedelta("0.5 sec") sj["事件开始时间"] = data.iloc[sj["事件起始编号"]-1,0].values- timeDel sj["事件结束时间"] = data.iloc[sj["事件终止编号"]-1,0].values + timeDel sj[\'洗浴时间点\'] = [i.hour for i in sj["事件开始时间"]] sj["总用水时长"] = np.int64(sj["事件结束时间"] - sj["事件开始时间"])/1000000000 + 1 # 构造用水停顿事件 # 构造特征“停顿开始时间”、“停顿结束时间” # 停顿开始时间指从有水流到无水流,停顿结束时间指从无水流到有水流 for i in range(len(data)-1): if (data.loc[i,"水流量"] != 0) & (data.loc[i + 1,"水流量"] == 0) : data.loc[i + 1,"停顿开始时间"] = data.loc[i +1, "发生时间"] - timeDel if (data.loc[i,"水流量"] == 0) & (data.loc[i + 1,"水流量"] != 0) : data.loc[i,"停顿结束时间"] = data.loc[i , "发生时间"] + timeDel # 提取停顿开始时间与结束时间所对应行号,放在数据框Stop中 indStopStart = data.index[data["停顿开始时间"].notnull()]+1 indStopEnd = data.index[data["停顿结束时间"].notnull()]+1 Stop = pd.DataFrame(data="停顿开始编号":indStopStart[:-1], "停顿结束编号":indStopEnd[1:]) # 计算停顿时长,并放在数据框stop中,停顿时长=停顿结束时间-停顿结束时间 Stop["停顿时长"] = np.int64(data.loc[indStopEnd[1:]-1,"停顿结束时间"].values- data.loc[indStopStart[:-1]-1,"停顿开始时间"].values)/1000000000 # 将每次停顿与事件匹配,停顿的开始时间要大于事件的开始时间, # 且停顿的结束时间要小于事件的结束时间 for i in range(len(sj)): Stop.loc[(Stop["停顿开始编号"] > sj.loc[i,"事件起始编号"]) & (Stop["停顿结束编号"] < sj.loc[i,"事件终止编号"]),"停顿归属事件"]=i+1 # 删除停顿次数为0的事件 Stop = Stop[Stop["停顿归属事件"].notnull()] # 构造特征 用水事件停顿总时长、停顿次数、停顿平均时长、 # 用水时长,用水/总时长 stopAgg = Stop.groupby("停顿归属事件").agg("停顿时长":sum,"停顿开始编号":len) sj.loc[stopAgg.index - 1,"总停顿时长"] = stopAgg.loc[:,"停顿时长"].values sj.loc[stopAgg.index-1,"停顿次数"] = stopAgg.loc[:,"停顿开始编号"].values sj.fillna(0,inplace=True) # 对缺失值用0插补 stopNo0 = sj["停顿次数"] != 0 # 判断用水事件是否存在停顿 sj.loc[stopNo0,"平均停顿时长"] = sj.loc[stopNo0,"总停顿时长"]/sj.loc[stopNo0,"停顿次数"] sj.fillna(0,inplace=True) # 对缺失值用0插补 sj["用水时长"] = sj["总用水时长"] - sj["总停顿时长"] # 定义特征用水时长 sj["用水/总时长"] = sj["用水时长"] / sj["总用水时长"] # 定义特征 用水/总时长 print(\'3127水事件用水时长与频率特征构造完成后数据的特征为:\\n\',sj.columns) print(\'3127用水事件用水时长与频率特征构造完成后数据的前5行5列特征为:\\n\', sj.iloc[:5,:5])
data["水流量"] = data["水流量"] / 60 # 原单位L/min,现转换为L/sec sj["总用水量"] = 0 # 给总用水量赋一个初始值0 for i in range(len(sj)): Start = sj.loc[i,"事件起始编号"]-1 End = sj.loc[i,"事件终止编号"]-1 if Start != End: for j in range(Start,End): if data.loc[j,"水流量"] != 0: sj.loc[i,"总用水量"] = (data.loc[j + 1,"发生时间"] - data.loc[j,"发生时间"]).seconds* \\ data.loc[j,"水流量"] + sj.loc[i,"总用水量"] sj.loc[i,"总用水量"] = sj.loc[i,"总用水量"] + data.loc[End,"水流量"] * 2 else: sj.loc[i,"总用水量"] = data.loc[Start,"水流量"] * 2 sj["平均水流量"] = sj["总用水量"] / sj["用水时长"] # 定义特征 平均水流量 # 构造特征:水流量波动 # 水流量波动=∑(((单次水流的值-平均水流量)^2)*持续时间)/用水时长 sj["水流量波动"] = 0 # 给水流量波动赋一个初始值0 for i in range(len(sj)): Start = sj.loc[i,"事件起始编号"] - 1 End = sj.loc[i,"事件终止编号"] - 1 for j in range(Start,End + 1): if data.loc[j,"水流量"] != 0: slbd = (data.loc[j,"水流量"] - sj.loc[i,"平均水流量"])**2 slsj = (data.loc[j + 1,"发生时间"] - data.loc[j,"发生时间"]).seconds sj.loc[i,"水流量波动"] = slbd * slsj + sj.loc[i,"水流量波动"] sj.loc[i,"水流量波动"] = sj.loc[i,"水流量波动"] / sj.loc[i,"用水时长"] # 构造特征:停顿时长波动 # 停顿时长波动=∑(((单次停顿时长-平均停顿时长)^2)*持续时间)/总停顿时长 sj["停顿时长波动"] = 0 # 给停顿时长波动赋一个初始值0 for i in range(len(sj)): if sj.loc[i,"停顿次数"] > 1: # 当停顿次数为0或1时,停顿时长波动值为0,故排除 for j in Stop.loc[Stop["停顿归属事件"] == (i+1),"停顿时长"].values: sj.loc[i,"停顿时长波动"] = ((j - sj.loc[i,"平均停顿时长"])**2) * j + \\ sj.loc[i,"停顿时长波动"] sj.loc[i,"停顿时长波动"] = sj.loc[i,"停顿时长波动"] / sj.loc[i,"总停顿时长"] print(\'3127用水量和波动特征构造完成后数据的特征为:\\n\',sj.columns) print(\'3127用水量和波动特征构造完成后数据的前5行5列特征为:\\n\',sj.iloc[:5,:5])
sj_bool = (sj[\'用水时长\'] >100) & (sj[\'总用水时长\'] > 120) & (sj[\'总用水量\'] > 5) sj_final = sj.loc[sj_bool,:] sj_final.to_excel(\'./sj_final.xlsx\',index=False) print(\'3127筛选出候选洗浴事件前的数据形状为:\',sj.shape) print(\'3127筛选出候选洗浴事件后的数据形状为:\',sj_final.shape)
import pandas as pd from sklearn.preprocessing import StandardScaler from sklearn.neural_network import MLPClassifier import joblib # 读取数据 Xtrain = pd.read_excel(\'./sj_final.xlsx\') ytrain = pd.read_excel(\'./water_heater_log.xlsx\') test = pd.read_excel(\'./test_data.xlsx\') # 训练集测试集区分。 x_train, x_test, y_train, y_test = Xtrain.iloc[:,5:],test.iloc[:,4:-1],\\ ytrain.iloc[:,-1],test.iloc[:,-1] # 标准化 stdScaler = StandardScaler().fit(x_train) x_stdtrain = stdScaler.transform(x_train) x_stdtest = stdScaler.transform(x_test) # 建立模型 bpnn = MLPClassifier(hidden_layer_sizes = (17,10), max_iter = 200, solver = \'lbfgs\',random_state=50) bpnn.fit(x_stdtrain, y_train) pre_y = bpnn.predict(x_stdtest) print(pre_y) # 保存模型 joblib.dump(bpnn,\'./water_heater_nnet.m\') print(\'3127构建的模型为:\\n\',bpnn)
import seaborn as sns from sklearn.metrics import accuracy_score, confusion_matrix import matplotlib.pyplot as plt C2=confusion_matrix(y_test, pre_y) # 注意到Scikit-Learn使用predict方法直接给出预测结果。 print(C2) #打印出来看看 # 2.2 根据混淆矩阵画热力图 sns.set() f,ax=plt.subplots(figsize=(5, 5)) sns.heatmap(C2, annot=True, fmt=".3g",ax=ax) # 画热力图,注意:默认fmt=".2g",此时图中的数据"144"会显示成"1.4e+02" ax.set_title(\'3127 confusion matrix\') # 标题 ax.set_xlabel(\'predict\') # x轴 ax.set_ylabel(\'true\') # y轴
from sklearn.metrics import classification_report from sklearn.metrics import roc_curve import joblib import matplotlib.pyplot as plt bpnn = joblib.load(\'./water_heater_nnet.m\') # 加载模型 y_pred = bpnn.predict(x_stdtest) # 返回预测结果 print(\'神经网络预测结果评价报告:\\n\',classification_report(y_test,y_pred)) # 绘制roc曲线图 plt.rcParams[\'font.sans-serif\'] = \'SimHei\' # 显示中文 plt.rcParams[\'axes.unicode_minus\'] = False # 显示负号 fpr, tpr, thresholds = roc_curve(y_pred,y_test) # 求出TPR和FPR plt.figure(figsize=(6,4)) # 创建画布 plt.plot(fpr,tpr) # 绘制曲线 plt.plot([0, 1], [0, 1], color=\'navy\', lw=2, linestyle=\'--\') # 辅助对角线 plt.title(\'3127用户用水事件识别ROC曲线\') # 标题 plt.xlabel(\'FPR\') # x轴标签 plt.ylabel(\'TPR\') # y轴标签 plt.savefig(\'./用户用水事件识别ROC曲线.png\') # 保存图片 plt.show() # 显示图形
Python 线程池模块,Python 多线程
Python 线程池模块,Python 多线程
相关知识
Python - Python操作mysql 数据库
Python - Python 简单爬取网页内容
Python - Python 操作文件
Python - Python函数
Python - Python3 列表
以上是关于python5的主要内容,如果未能解决你的问题,请参考以下文章