2023-04-09 有向图及相关算法
Posted 空無一悟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2023-04-09 有向图及相关算法相关的知识,希望对你有一定的参考价值。
有向图及相关算法
1 有向图的实现
有向图的的应用场景
- 社交网络中的关注
- 互联网连接
- 程序模块的引用
- 任务调度
- 学习计划
- 食物链
- 论文引用
- 无向图是特殊的有向图,即每条边都是双向的
改进Graph和WeightedGraph类使之支持有向图
2 有向图算法
有些问题,在有向图中不存在,或者我们通常不考虑
- floodfill
- 最小生成树
- 桥和割点
- 二分图检测
有些问题,在无向图和有向图中是一样的
- DFS的代码迁移到有向图完全不用改,测试代码
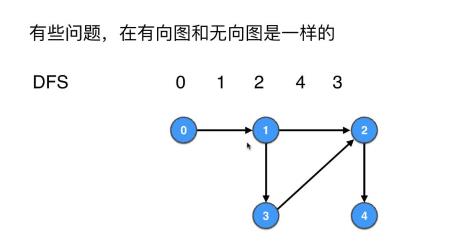
- BFS的代码迁移到有向图完全不用改,测试代码
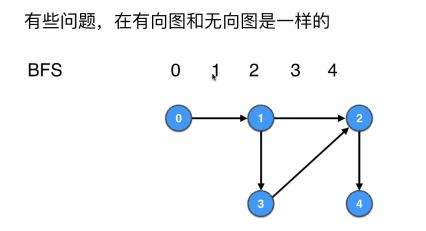
- BFS用来求无向无权图最短路径的代码用来求
有向无权图也完全不用改
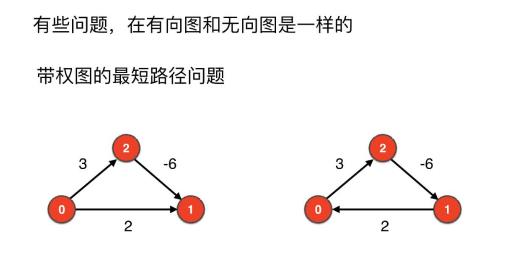
有向有权图的最短路径
无向有权图有负权边一定有负权环;有向有权图有负权边不一定有负权环。所以最短路径问题针对有负权边的无向有权图没有意义,但是对有负权边的有向有权图可能是有意义地。
上面图片中,左右两边都是有向有权图,左边的图不存在负权环,右边的图就存在负权环,所以有向有权图中有负权边不一定有负权环
3 有向图环检测和DAG
原理
无向图中的环的判定方法在有向图中不适用,通过在遍历过程中添加标记即可,递归回退时取消对应顶点的标记
实现
有向图环检测的现实意义
现实中很多场景都是追求
有向无环图(Directed Acyclic Graph即DAG)的
- 程序模块的循环引用检测
- 任务调度冲突检测
- 学习计划
4 有向图的度:入度和出度
举例
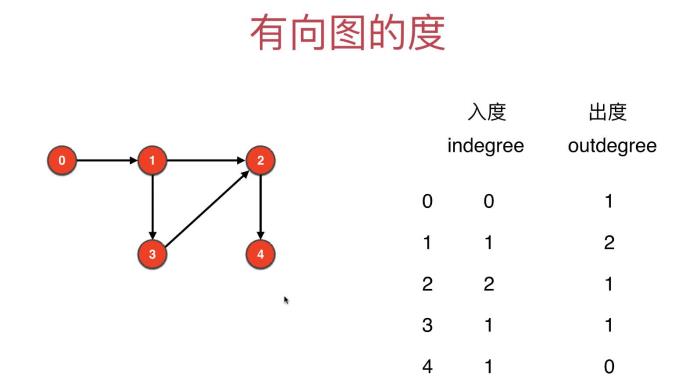
对Graph类的修改和测试
5 有向图求解欧拉回路
和无向图进行比较
| 对比项 | 无向图 | 有向图 |
|---|---|---|
| 存在欧拉回路的充要条件 | 每个点的度数为偶数 | 每个点的入度等于出度 |
寻找有向图欧拉回路的代码
寻找欧拉路径的充要条件
主要是无向图和有向图的对比
| 对比项 | 无向图 | 有向图 |
|---|---|---|
| 存在欧拉路径的充要条件 | 除了两个点(起始点和终止点)两个点的度数为奇数,其余每个点的度数为偶数 | 除了两个点(起始点和终止点),其余每个点的入度等于出度。这两个点,起始点出度比入度大1,终止点入度比出度大1 |
6~7 拓扑排序--仅针对有向图
拓扑排序的定义和应用价值
- 定义:在一个有向图中,对所有的节点进行排序,要求没有一个节点指向它前面的节点,最终的排序结果就是拓扑排序
- 价值:当现实中存在图状约束时,要你给出一个约束下可行的图遍历方便,这个时候拓扑排序就用上了~比如选课、选旅游路线等
原理
删除入度为0的顶点,然后删除这个和顶点连接的边,更新剩下顶点的入度;然后再删除剩下顶点中入度为0的顶点,删除这个顶点和这个顶点连接的边,更新剩下顶点的入度....一直到图中没顶点,拓扑排序就完成了,按照删除顺序得到的顶点列表就是拓扑排序结果。
过程模拟(不短寻找、删除和更新入度为0的顶点)
- 1.初始化计算得到各个顶点的入度inDegrees数组

- 2.删除此时图中入度为0的顶点即顶点0,并删除和顶点0相连的边
0->1,更新删除边影响的其他顶点的入度,即把顶点1的入度更新为0
- 3.删除此时图中入度为0的顶点即顶点1,并删除和顶点1相连的边
1->2、1->3,更新删除边影响的其他顶点的入度,即把顶点2的入度更新为1、顶点3的入度更新为0
- 4.删除此时图中入度为0的顶点即顶点3,并删除和顶点3相连的边
3->2,更新删除边影响的其他顶点的入度,即把顶点2的入度更新为0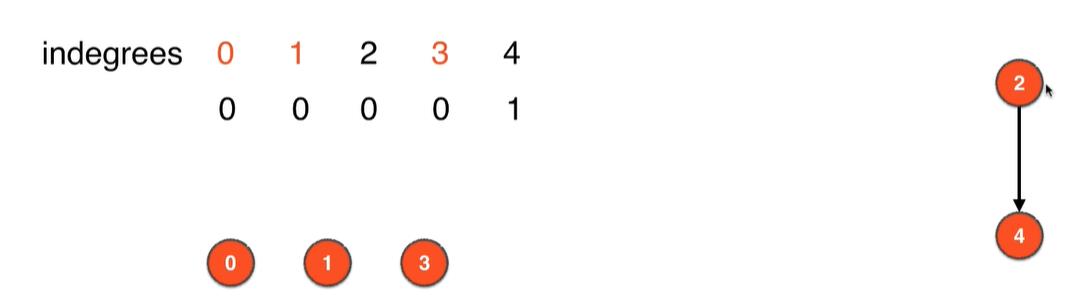
- 5.删除此时图中入度为0的顶点即顶点2,并删除和顶点2相连的边
2->4,更新删除边影响的其他顶点的入度,即把顶点4的入度更新为0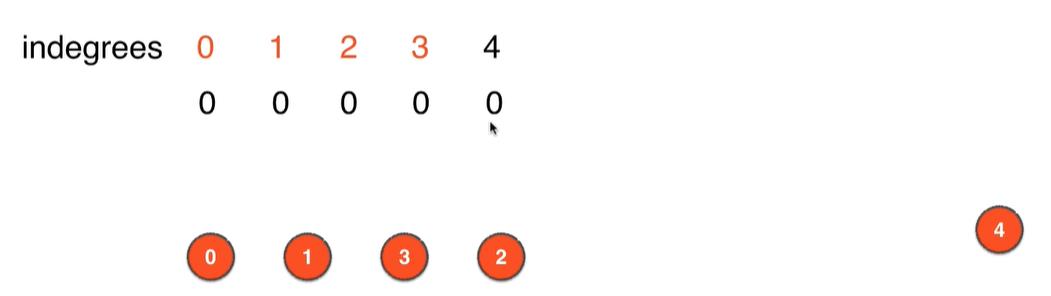
- 6.删除此时图中入度为0的顶点即顶点4,此时图中已经没有顶点,拓扑排序完成,上面节点删除的顺序即拓扑排序的结果,即[0, 1, 3, 2, 4]
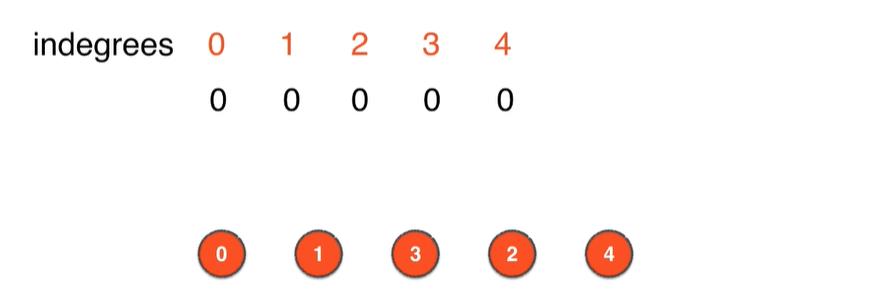
代码实现侧层面的优化
- 删除边和点不一定要真删除,可以深度clone后只更新入度即可~
- 使用队列记录当前入度为0的顶点,每次更新入度值时一般会把一个以上的更新后入度为0的顶点放入一个队列,每次从队列中取出一个点作为拓扑排序的下一个定点
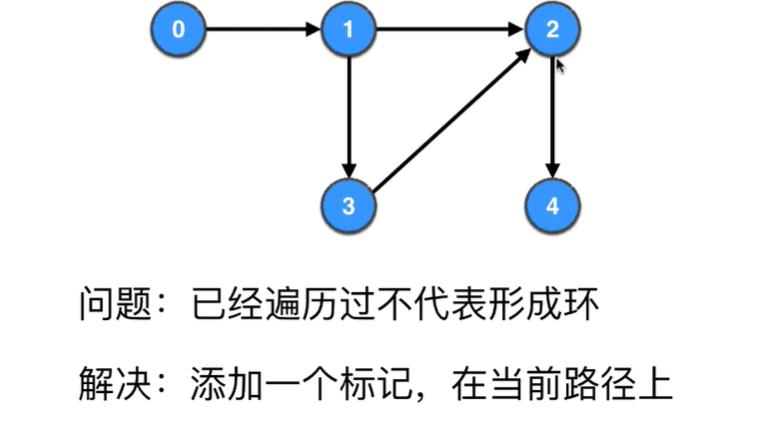
拓扑排序可能无解
如下图,相当于1、2、3有循环依赖的关系虽然此时拓扑排序无解,但是正好可以用于有向图的环检测。只有`有向无环图即DAG`才有拓扑排序
代码实现
LeetCode上的相关题目
8~9 拓扑排序的另一种方法,方便后续学习有向图的强联通分量
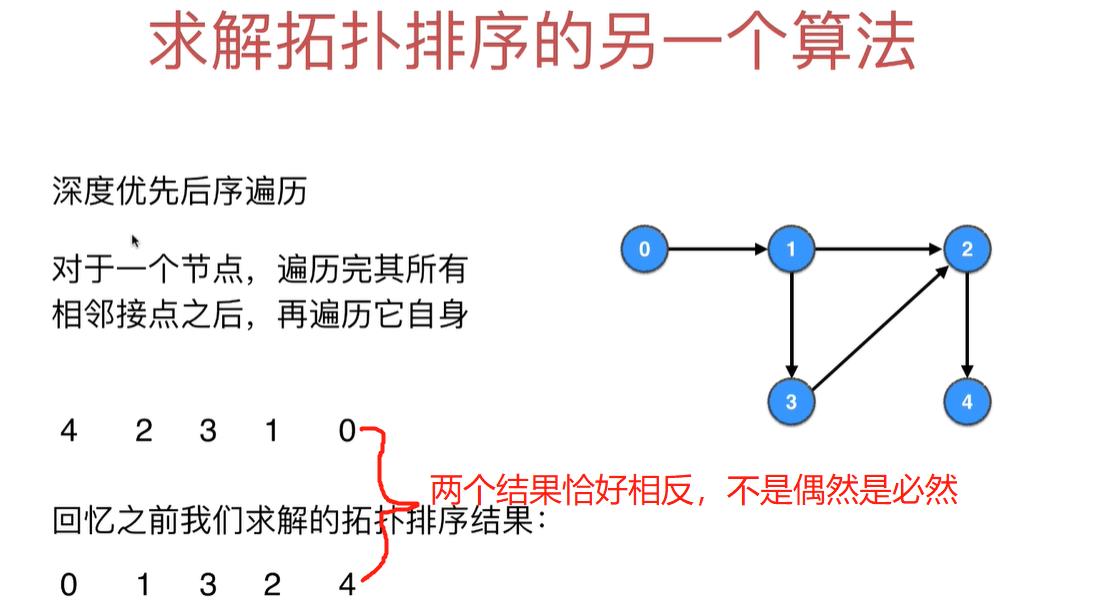
用到了图的DFS的后序遍历,自己复习下
重要结论:深度优先后续遍历的逆序就是拓扑排序的结果
缺点是不能做环检测,所以我们给这个算法的图必须是有向无环图
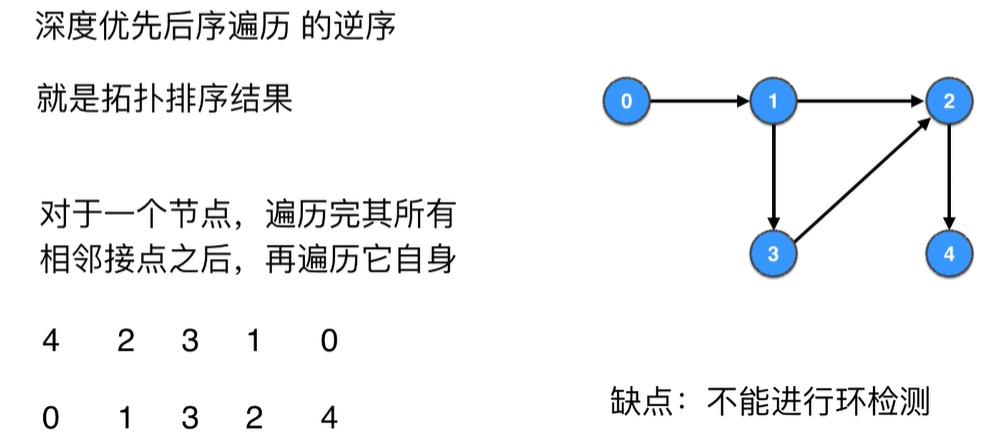
代码实现和测试
太简单,直接调用前面的图的DFS的后序遍历代码了
10~12 有向图的强联通分量
有向图因为有方向,相似的的图对无向图是连通图,对有向图就不是
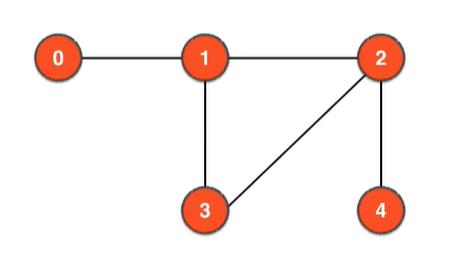
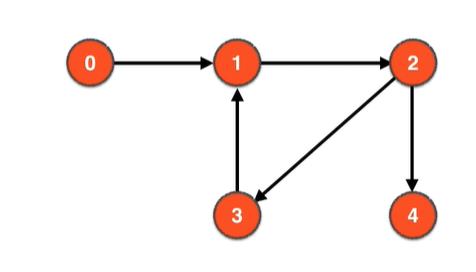
有向图的强联通分量
在一个有向图中,任何两点都可达的联通分量就叫强联通分量。如下图中的1、2、3组成强联通分量
将所有强联通分量看做一个点,得到的图一定是DAG(有向无环图)
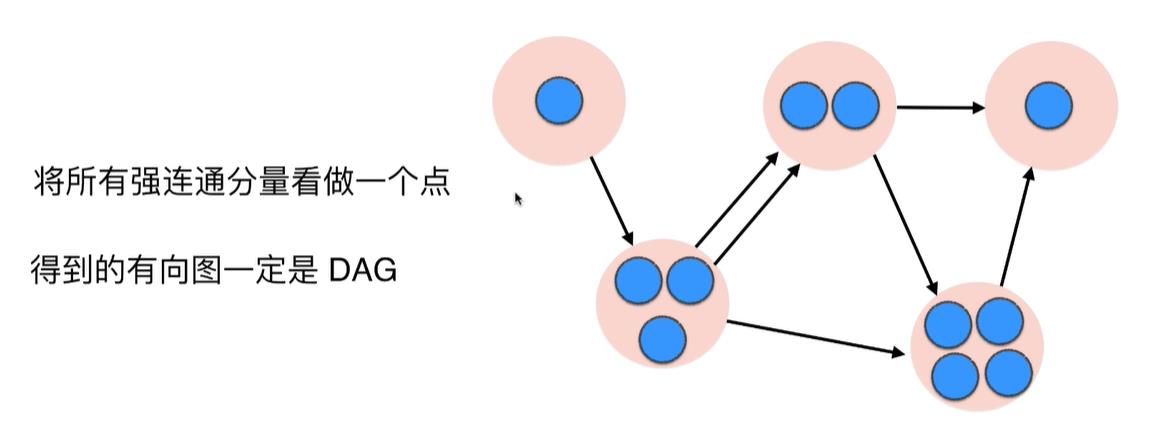
证明:反证法,如果有几个强联通分量看做的点组成了环,那么这个环还可以一个强联通分量,和我们最初的假设"所有的强联通分量各自看做一个点"矛盾。
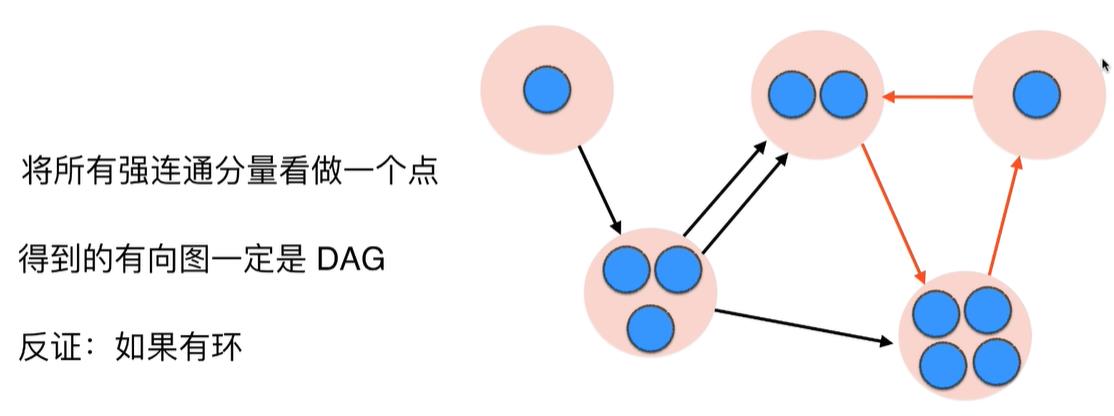
求强联通分量各自含有的点和一共有的强联通分量个数
DFS一旦走入一个强联通分量就出不来(因为每个强联通分量一定是个环,DFS只会在环里绕圈)~~可以作为找到一个强联通分量的标志
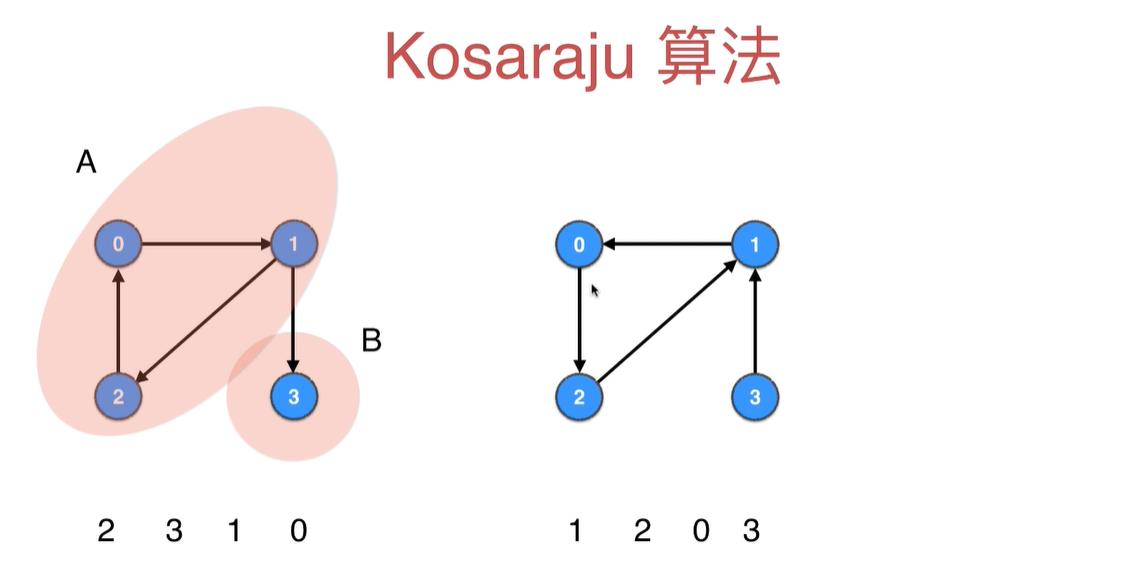
11~12 Kosaraju算法
为了解决DFS后序遍历不是我们想要的强联通分量各自分开的结果
我们上来先把原有的图每条边进行反向处理(v->w)变成(w->v),在进行DFS后序遍历的结果就是我们想要地了
Kosaraju算法阐述
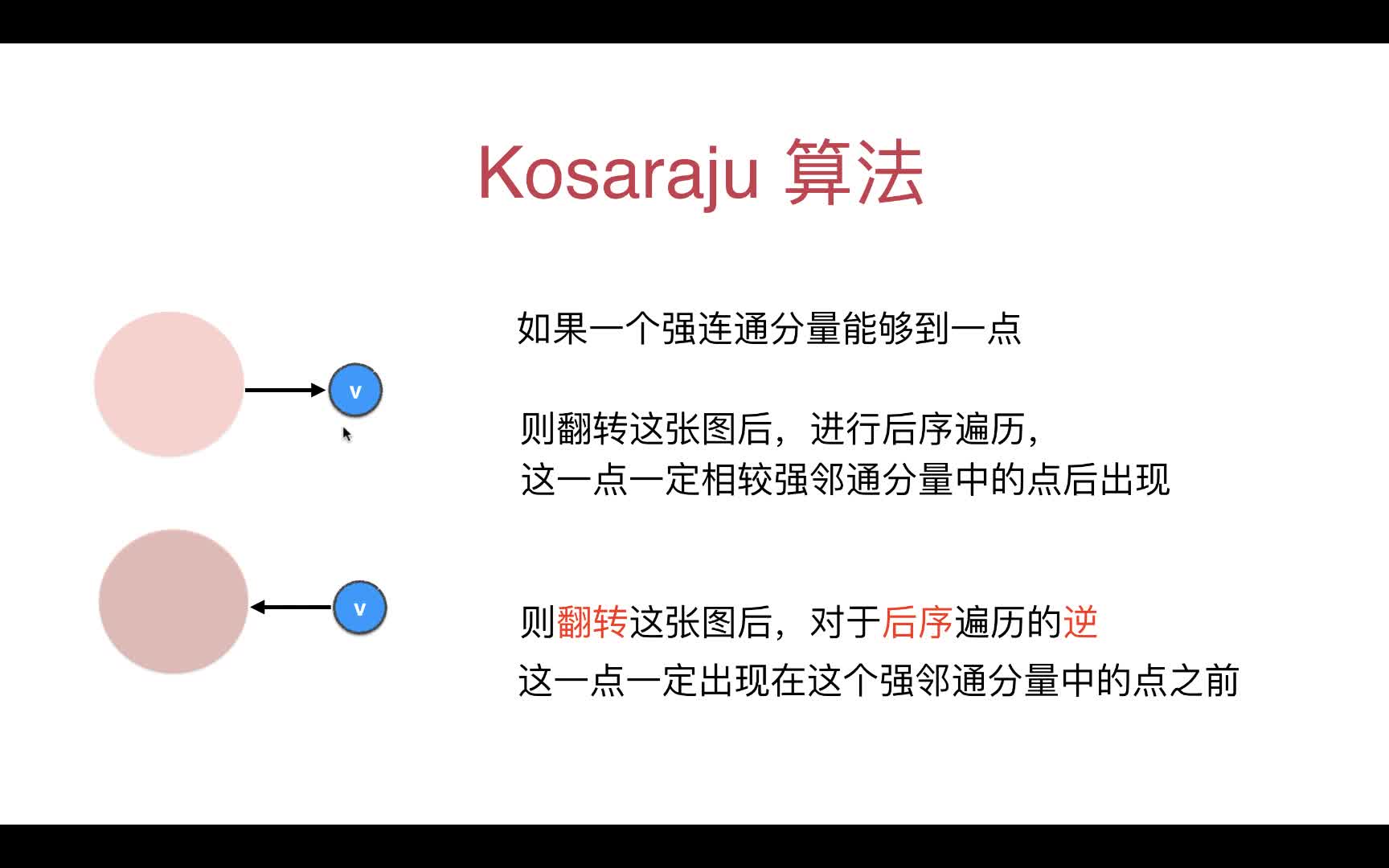
举例如下:
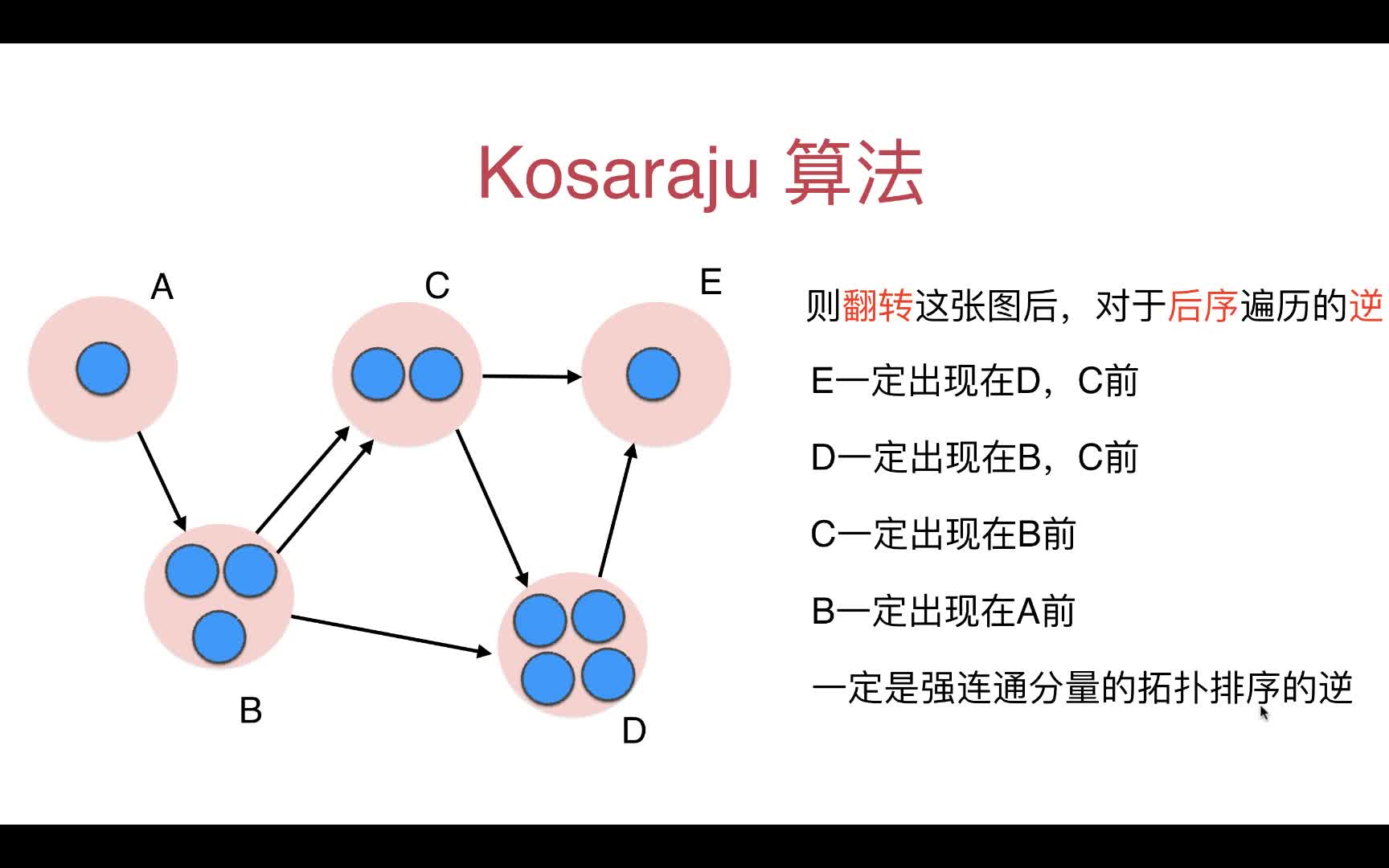
代码实现:略
后面有需要再搞吧
13 有向图算法总结
在无向图中存在,但是在有向图中不存在或者我们通常不考虑地
- floodfill
- 最小生成树
- 桥和割点
- 二分图检测
在有向图和无向图中完全一样的算法
- DFS、BFS
- 最短路径:Dijkstra
- 最短路径:Bellman-Ford
- 最短路径:Floyd
有向图和无向图不一样的算法
- 有向图的环检测
- 有向图的度
- 欧拉回路、欧拉路径
有向图特有的问题
- 拓扑排序:TopoSort
- 入度+队列实现
- 顺便做环检测
- 时间复杂度O(V+E)
- 强联通分量
- Kosaraju算法,简单说就是反图的DFS后续的逆序做CC
- 时间复杂度是O(V+E)
算法笔记图结构及图的 DFS 和 BFS 介绍
前言: 该篇文章将介绍如何应付面试中的图结构,并且还简单介绍了 BFS 和 DFS
文章目录
1. 图的基本介绍
基本概念:
- 图由点的集合和边的集合构成
- 虽然存在有向图和无向图的概念,但实际上都可以用有向图来表达
- 边上可能带有权值
图的结构:
- 邻接表法
- 邻接矩阵法
- 还有其它众多的方式
如何搞定图的面试题: 图的算法都不难,但是写代码时会很复杂,coding 代价比较高,因此可以通过以下的方式来应付图的面试题
- 先用自己最熟练的方式,实现图结构的表达
- 在自己熟悉的结构上,实现所有常用图的算法作为模板
- 把面试题提供的图结构转化为自己熟悉的图结构,再调用模板或改写即可(做一个适配器)
2. 图的实现
实现代码:
-
点结构的实现
import java.util.ArrayList; // 点结构的描述 public class Node // 该点的值 public int value; // 该点的入度数 public int in; // 该点的出度数 public int out; // 该点的相邻点(指该点指向的点) public ArrayList<Node> nexts; // 该点的相邻边(指该点指向的边) public ArrayList<Node> edges; public Node(int value) this.value = value; in = 0; out = 0; nexts = new ArrayList<>(); edges = new ArrayList<>(); -
边结构的实现
// 边结构的描述 public class Edge // 边的权重 public int weight; // 入边节点 public Node from; // 出边节点 public Node to; public Edge(int weight, Node from, Node to) this.weight = weight; this.from = from; this.to = to; -
图结构的实现
import java.util.HashMap; import java.util.HashSet; // 图的描述 public class Graph // 点的集合,Integer 表示节点的值,先有值,再创建节点 public HashMap<Integer, Node> nodes; // 边的集合 public HashSet<Edge> edges; public Graph() nodes = new HashMap<>(); edges = new HashSet<>();
常见面试题的图结构:
- 用一个二维数组表示,每个一维数组里面有三个值
- 第一个值表示边的权重
- 第二个值表示边的出发节点
- 第三个值表示边的目的节点
假设现有一个数组表示是这样的:3, 0, 7, 5, 1, 2, 6, 2, 7,它符合上面图的结构,那么它用图表示如下

当我们面试遇见这种结构的图时,就可以使用我们上述已经定义好的图的结构来表示,因此我们只需要再做一个适配的过程
适配代码:
public class Create
public static Graph createGraph(int[][] matrix)
Graph graph=new Graph();
for(int i=0;i<matrix.length;i++)
// 边的权重
int weight=matrix[i][0];
// 出发节点的值
int from=matrix[i][1];
// 目的节点的值
int to=matrix[i][2];
// 如果该图中还没有包含该节点,则将节点入图
if(!graph.nodes.containsKey(from))
graph.nodes.put(from, new Node(from));
if(!graph.nodes.containsKey(to))
graph.nodes.put(to, new Node(to));
Node fromNode=graph.nodes.get(from);
Node toNode=graph.nodes.get(to);
Edge edge=new Edge(weight,fromNode,toNode);
fromNode.out++;
toNode.in++;
fromNode.nexts.add(toNode);
fromNode.edges.add(edge);
graph.edges.add(edge);
return graph;
3. BFS
BFS 方式:
从图中弹出最高层的节点,用一个集合 Set 注册该节点,然后将该节点入队列。当我们从队列中将它弹出时,将它的相邻节点(指向的节点)进行入队列,但是首先需要判断相邻节点是否在集合中注册,如果注册了,就不做处理;如果未注册,就进行注册,并将该节点进行入队列。然后重复刚刚的操作,对每层进行遍历
方法模板:
import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;
public class BFS
// BFS 需要有一个头节点
public static void bfs(Node start)
if (start == null)
return;
Queue<Node> queue = new LinkedList<>();
HashSet<Node> set = new HashSet<>();
queue.add(start);
set.add(start);
while (!queue.isEmpty())
Node node = queue.poll();
System.out.println(node.value);
for (Node cur : node.nexts)
if (!set.contains(cur))
set.add(cur);
queue.add(cur);
4. DFS
DFS 方式:
一条路走到底为止,但是不能形成环路,当到底为止后,就返回上一个节点,如果该节点没有其它路,就继续往上。当某个节点还有其它路,先判断新的节点是否已经打印果过,打印过就继续往上,直到找到新的节点且未打印过。当最终返回头节点,则深度遍历结束。其中使用集合 Set 来标记该节点是否走过或打印过,使用栈来存储当前遍历路线的节点
方法模板:
import java.util.HashSet;
import java.util.Stack;
public class DFS
public static void dfs(Node node)
if (node == null)
return;
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
stack.add(node);
set.add(node);
// 在入栈时就进行打印
System.out.println(node.value);
while (!stack.isEmpty())
Node cur = stack.pop();
for (Node next : cur.nexts)
if (!set.contains(next))
stack.add(cur);
stack.add(next);
set.add(next);
System.out.println(next.value);
break;
以上是关于2023-04-09 有向图及相关算法的主要内容,如果未能解决你的问题,请参考以下文章