谨慎看待统计中的P值、置信区间和统计功效
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了谨慎看待统计中的P值、置信区间和统计功效相关的知识,希望对你有一定的参考价值。
参考技术A 假设测试一种新感冒药,新药可以确保一天之内去除所有的感冒症状,如何验证新药效果?为了验证新药效果,设计实验来检验药效,实验如下:
找到20位感冒患者,分两组,其中一组服用新药,另一组服用安慰剂。记录他们的感冒时长,找到两组患者的平均感冒时长。
实验中的问题:
我们知道,并不是所有的感冒都持续同样的时间。有可能服药的组都是较短的感冒患者,而服用安慰剂的组都是较长时间的感冒患者,那么如何证明药物有效,而不是运气?
利用统计的假设检验解决此问题的方法
若知道典型的感冒分布(也就是多少感冒是短期、长期感冒已经平均感冒时长),可以设计实验检验假设,通过实验,给出其中一组随机样本患者的感冒时长比平均时长更长或更短的概率。
假设检验方法(显著性检验):即使药物完全无效,那么实验产生以上观测结果的可能性多大? 这个可能性就是P值 。
若只对一个人实验,感冒康复速度是快还是慢是不足为奇的。但是1000万个患者进行测试,而所有患者都是短期感冒,这种情况就不太可能是巧合了,更有可能是药物的效果。
分组对照试验,假设药物效果没有真实差异的情况下,差异等于甚至大于实际观测值的概率。
如:给100个患者服药,发现他们平均感冒时长比对照组少一天,这时P就是在药物无效的假设下,只少1天有可能是巧合,可能的猜测是,P依赖于效果大小,也和样本数量相关。
P值不是衡量正确性或重要性的,而是衡量“意外”,P越小,实验结果是运气的可能性越大。
如何用P来解释分组之间是否有差异?
若 P < 0.05,认为分组间有差异。(也称为统计显著性)
**注意:0.05是人为经验,实际使用中要谨慎。**
应用P值时,假设各组之间没有区别。这是显著性检验的一个反直觉的特征:如果想要证明有效,那就证明数据不支持无效。因此,P值可以扩展到任何一种用数学表示某个要推翻的假设情形。
1. 统计显著性不意味着任何实际意义的显著性。统计显著性有可能是噪声,或者真实有效的,需要更多的数据才能确定。
2. 没有数学工具可以判断假设是真是假:也可考虑假设与数据是否一致。如果数据太少或者不清楚,那么结论也就不对了。
两种不同的实验设计可以产生相同的观测数据,但不有不同的P值,因为观测数据是不同的。
实验1:若连续12个布尔问题,正确回答了9个。
检验假设:是否随机猜对了这些问题?
利用二项分布,计算得P = 0.073, P > 0.05,很有可能是随机猜的答案。
实验2:若有无限个问题,直到答错3个。现在计算在15、20、175、231个题目后没有答错3个的概率。
检验假设:是否随机猜对了这些问题?
计算得 P = 0.033,P < 0.05,于是得出依靠猜测答题的可能性不高。
** 注意:两个实验收集到相同数据,但是却有不一样的结论。 **
控制假设性检验的2类错误至关重要
1. 将无效认为有效。由于我们过于激进。
2. 将有效认为无效。由于我们过于保守。
给出一种规范的 决策过程 来确保第一类错误(将无效认为有效)的可能性只在预先确定的比率下发生。这个比率成为显著性水平α,实验者可以依据经验和期望的基础上设置合适的α。
为了比较那种α设置的最好,可以检测在给定α的条件下,哪一种实验过程犯第二类错误的比率最低。
实际做法
1. 定义一个原假设,比如假设药物无效;同时定义一个备选假设,如有效。
2. 构建实验比较2种假设,并且决定在原假设正确的时候我们期望的结果。
3. 如果P < α,拒绝原假设。** 注意:P值的大小,除了拒绝原假设外,无法用来表示任何其他结论。 **
仅仅通过1次实验不能得到第一类错误率。它是由检验过程决定的,而不是由一次实验的结果得出的。当用一个检验过程获得一个长期的第一类错误率α,不管结果怎样,都不能确定每次实验都有一个真实的P值和对应的第一类错误率。
P值不是测度意外的唯一方法,置信区间也可以,同时可以提供更多的信息。
如果想检验效应是否显著区别于0,可以建立一个95%的置信区间来检验这个区间是否包含0。在此过程中,可额外的知道估计的精确度。
如果置信区间太宽,则需要更多的数据。
置信区间的表示大于P值显著性检验的效果。如果能做置信区间,最好做。
一个狭窄的包含0的置信区间:表明效应可能比较小。
一个较宽的包含0的置信区间:表明测量值并不十分精确,不足以做出结论。
要理解置信区间,首先要理解总体和样本的关系。假设一锅汤是总体,我们为了知道汤的味道,用勺子打了一小勺,这一小勺即是样本。一小勺能否正确反映出整锅汤的味道往往取决于汤是否均匀搅拌,放在统计学里则是有没有随机抽样。
同样用一个例子理解置信区间。假设我们想知道某一个中学男生的平均身高,有两种方法:
1. 暴力方法:找出该中学的所有男生,记录他们的身高,求平均值。这种方法虽然准确,单成本巨大,实际上无法操作。
2. 统计方法:随机抽100个男生作为样本,由这100个男生的身高平均值(估计值)来估算该中学男生的平均身高(真实值)。
用统计方法时,最容易想到是拿这100个男生的身高平均值作为该中学所有男生的身高平均值。但是用一个固定数值来作为推断结果很容易出错。况且抽样样本不同,所得到的平均身高肯定也会不同。这时候,统计学家们想到了一个狡猾的办法,就是用一个数值区间来表示推断结果。一个区间内包含真实值的概率当然大大增加。这里这个区间即为置信区间。但是因为抽样不同,我们获得的置信区间也会不一样。假设我们抽样了100次(每一次抽100个男生),那么我们可以获得100个不同的置信区间。95%置信区间表示的是,这100个置信区间中,有95个以上的区间包含了该中学男生的平均身高的真实值。
容易产生的误区: 95%置信区间表示真实值有95%的概率落到当前置信区间之内。这个说法是不准确的,真实值要么在区间内,要么不在区间之内。95%的置信区间表示,多次抽样所得到的多个置信区间里,包含真实值的区间占比。
由于数据不足,容易犯1类错误或者2类错误。收集多少数据合适呢? 统计功效用来解决这个问题。它能将某种强度的效应从纯粹的运气因素里区分并识别出来的概率。
** 注意:人为的将统计功效设为80%,又是人为经验,实际中要谨慎。 **
假设检验的功效是指产生统计显著性效果(P < 0.05)的概率。对于一个均匀硬币,抛100次,40-60次正面向上的概率为95%,因此,若检验一枚不均匀的硬币,检验功效是指这枚硬币正面向上的次数落在区间(40,60)以外的概率。
有3种因素影响统计功效:
1. 偏差大小:硬币越是不均匀,越容易检测出来。
2. 样本容量:如果足够大,就算细微的偏差也能检测出来。
3. 测量误差:如果不是硬币,而是医学药物就很难获得指标测量。
** 注意:把 P < 0.05当做检验假设的标准,均匀硬币可以,非均匀硬币一样有可能(小的样本容量可能性就越高) **
1. 设计实验是,先计算统计功效,以此来决定所需样本的大小。
2. 如果想精确的度量某种效应,不要单纯的使用显著性检验,更好的做法是设计置信度使用,获得置信区间。
3. 统计上不显著并非意味着0。即使结果是不显著的,该结果也代表基于所收集的数据所得的估计。“不显著”与“不存在”并不等价。
4. 持怀疑态度看统计功效的结论,这些结论可能夸大。
5. 比较规模不同的组时,计算置信区间。置信区间可以反应估计的精确度:规模较大的组置信区间较窄,估计更精确。
收集不到足够的样本量,从而将单个样本的考察次数增加,这样是不行的。
如:收集2000名高血压病患者,比较新药,分为2组,每组1000人,过了统计功效的数目。是可信的。但是实际中找不到2000个人,于是找了100个人,每个人做了10次血压测量,就错了。
** 注意:实验设计中,牢记消除数据相关性 **
如果不能消除相关性,可以采用以下几种方法近似处理:
1. 对有相关性的数据进行平均处理。
2. 单独分析有相关性的数据。
3. 调整P值和置信区间。
1. 确保统计分析回答了要研究的问题。与之前数据高度相关的重复测量数据,并不能证明结论可以推广到更一般的群体。这些数据只是增加了样本的确定性。
2. 使用分层模型和集群标准误这样的统计方法,可以处理数据间的相依性。
3. 设计实验时最好消除变量间的相关性,如不能消除相关性,最好记录混杂因素,在统计上处理。
一个统计意义不显著的结果,并不意味着两者之间没有差异。但是,一个统计意义显著的结果也不意味着一定存在差异。
P值实在假设无效的情况下,检验统计量取当前及更加极端值的概率,而不是有效的可靠性。
判断有效的时候,先考虑基础概率,而不是特殊案例。
1. P < 0.05 并不等于结果错误的可能性为5%。
2. 如果进行多重假设检验,或者寻找多个变量间的相关性,应用Bonferroni修正或者Benjamini-Hochberg修正,控制过多的假阳性。
3. 如果某一领域经常进行多重假设检验,就需要学习专门的技术来处理数据。
4. 使用基础概率的先验估值计算某一给定的结果是假阳性的概率。
[概率论与数理统计]笔记:5.3 置信区间
 记录置信区间的相关概念,以及关于正态总体参数的置信区间的公式总结。
记录置信区间的相关概念,以及关于正态总体参数的置信区间的公式总结。
5.3 置信区间
前言
点估计无法提供其估计的误差,而区间估计可以。
案例:“某人的月薪比2k多,比20k少”,这就是一个区间估计。
区间估计的好坏有两个衡量指标:
- 区间长度
- 真实值落在该区间的概率
我们希望区间长度足够小,而真实值落在该区间的概率又足够大。
事实上,这两个指标是矛盾的,如果概率很大,会导致区间变大;如果区间长度变小,落在区间内的概率就会变小。
定义
- \\(\\theta\\)是要估计的参数。
- \\((\\underline\\theta,\\overline\\theta)\\)是置信区间,其中\\(\\underline\\theta\\)是置信下限,\\(\\overline\\theta\\)是置信上限。
- \\(1-\\alpha\\)是置信水平,或者叫置信度。
做题的时候一般是题目告知置信度,然后需要求解置信上下限。
表述
\\((\\underline\\theta,\\overline\\theta)\\)能套住\\(\\theta\\)的概率是\\(1-\\alpha\\)。
这里需要区分两种表述:
- \\((\\underline\\theta,\\overline\\theta)\\)能套住\\(\\theta\\)的概率是\\(1-\\alpha\\)。
- \\(\\theta\\) 落在 \\((\\underline\\theta,\\overline\\theta)\\)的概率是\\(1-\\alpha\\)。
需要明确的是,\\(\\theta\\)虽然是未知的,但是是确定的。\\(\\theta\\)准确地固定在数轴上的一个位置,只是我们不知道在哪里。我们使用区间\\((\\underline\\theta,\\overline\\theta)\\)来做多次试验,每次试验的区间是随机的不同的,因此\\(\\theta\\)有时会被区间套住,有时候不会。
因此,我们使用的表述是套住,而不是落在。后者是针对不确定的值时候的表述。
枢轴变量
定义
为了求解置信区间,需要构造枢轴变量
其中\\(\\theta\\)是未知参数,\\(T\\)是已知的,\\(I\\) 的分布已知且与\\(\\theta\\)无关。
对于给定的\\(1-\\alpha\\),确定\\(F\\)的上\\(\\frac\\alpha2\\)分位数,记为\\(u_\\frac\\alpha2\\);确定\\(F\\)的上\\((1-\\frac\\alpha2)\\)分位数,记为\\(u_1-\\frac\\alpha2\\),那么就会有
图解
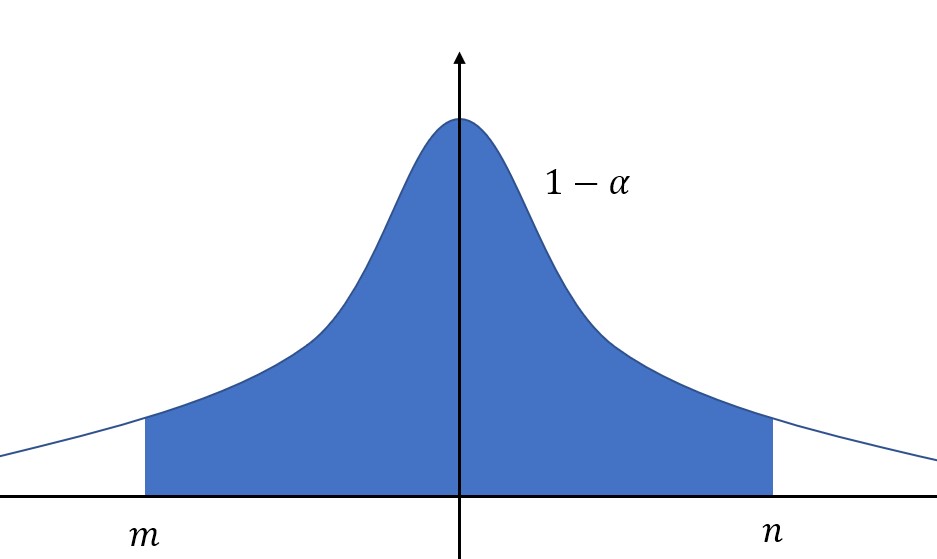
对于给定的置信度,也就是概率\\(1-\\alpha\\),我们的目的是求解区间上下限,也就是图中的\\(m\\)和\\(n\\)。
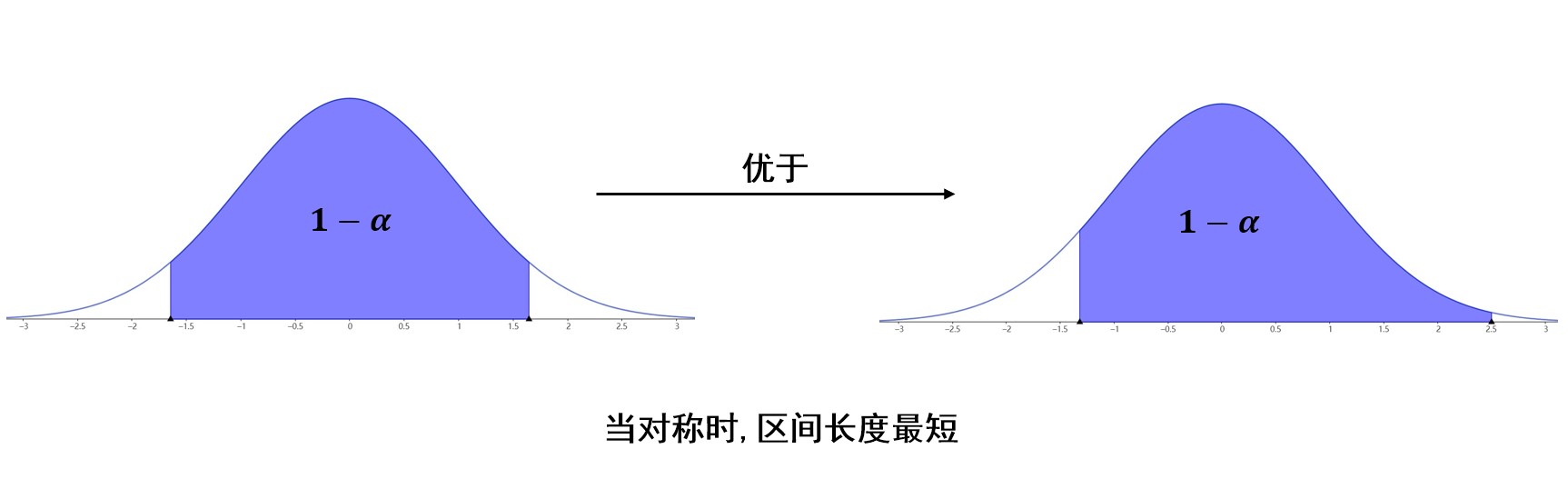
值得注意的是,我们希望区间长度小一些,如果研究的分布是正态分布,或者密度函数类似于上图,那么在置信度一定的情况下,即图中蓝色区域面积一定,只要选定区间位于中间,关于\\(y\\)轴对称,那么区间长度就是最小的。(因为峰值在中间)
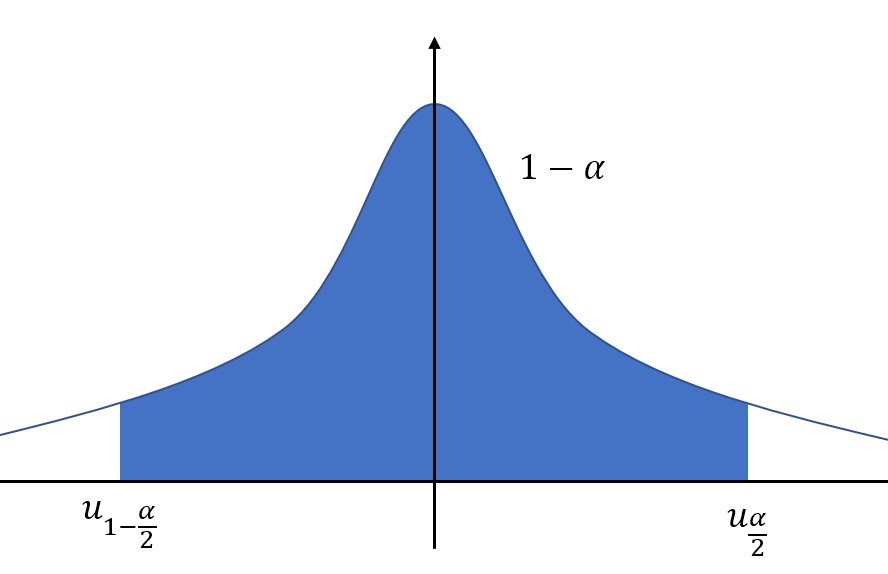
当置信区间位于中间时,置信度为\\(1-\\alpha\\),那么左右两个置信上下限就可以通过上侧分位数表示了。
中间的阴影面积为\\(1-\\alpha\\),那么左右两侧的空白面积就分别是\\(\\frac\\alpha2\\)。
置信上限使用上侧分位数表示就是:\\(u_\\frac\\alpha2\\).
置信下限使用上侧分位数表示就是:\\(u_1-\\frac\\alpha2\\).
总结
构造枢轴变量的目的是为了求解置信区间,将枢轴变量构造成我们熟悉的分布,比如正态分布,\\(t\\)分布,\\(F\\)分布。然后就可以利用这些分布的性质列出不等式,然后求解出我们要估计的参数的区间。
需要注意的是,枢轴变量只能包含一个未知的参数,即我们要估计的参数\\(\\theta\\),只有这样才能进行不等式化简。
正态总体参数的置信区间
均值\\(\\mu\\)的置信区间
情况1:方差\\(\\sigma^2\\)已知
总体方差\\(\\sigma^2\\)已知,估计\\(\\mu\\),此时\\(\\mu\\)是未知参数。
构造枢轴量:
相关知识点:
以上是关于谨慎看待统计中的P值、置信区间和统计功效的主要内容,如果未能解决你的问题,请参考以下文章