CS231N assignment 1 _ SVM 学习笔记 & 解析
Posted 360MEMZ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CS231N assignment 1 _ SVM 学习笔记 & 解析相关的知识,希望对你有一定的参考价值。
SVM的相关概念
首先如课程所说, 本质上线性分类器就是对一个图片向量到打分向量的映射,所以就是ωx+b=S.

对于最基本的二分类SVM, 其利用超平面划分了点集,结果非黑即白, 但是现在我们利用的W可以认为是好几个超平面在一起,得到的不再是一个结果,而是打分向量,如果只需要打分判断正确类别就行,是SVM的思路, 而需要正确类别得分尽可能高, 则需要softmax. 课程内说, 虽然二者科研上区别不是很大, 但是我们要记住这个结论.
SVM的一个样本的损失函数定义为: S就是前面的每个类别打分
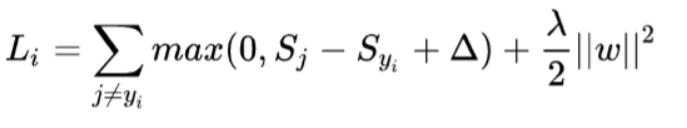
前面的max项实际上就是现在的SVM相比于二分类SVM多出来的项目, 但是意义却很不一样, 前者是分类的错误损失, 后者是我们希望ω尽可能简单做的惩罚系数, 这里是L2范数, 课程提到了L1系数, L2可以防止结果ω对于个别元素的权重过大, 而L1可以使得ω相对稀疏.
上面的Δ取值一般取做1,因为Δ增大减小, 实际上可以通过ω的缩放来实现.
直观理解和预处理的技巧
这里的直观理解真的觉得很妙. 对于CIFAR中, ω尺寸为10*3072, 而图像为3072*1(这里将图像视为列向量), 这样ω就很像是10个图像向量转置形成的矩阵了. 所以我们可以将ω的10行看作是图像的模板:

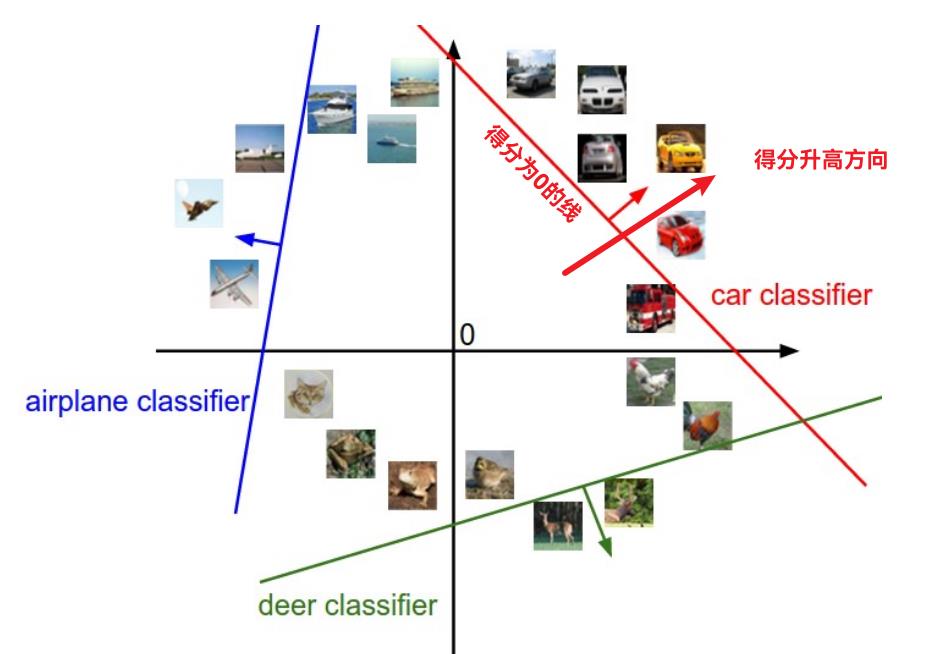
此外, ω也可以视作图像空间的超平面, 这个平面上该项打分为0, 在某个方向得分越高. 这个和二分类SVM很像, 但是因为这里类别增多了, 所以一项打分增大不能反应其他项的情况.
下面是实际训练的一些注意事项. 为了让偏置项不必考虑, 我们给图片最后一项加上常数1, 并将b加入到ω内, 这样ω尺寸变为10*3073.
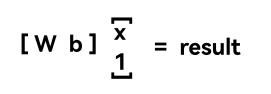
我们还需要正则化图像, 也就是减去平均值, 这样图像取值关于0对称, 防止所有项的打分都非常高. 总之, 机器学习中归一化非常重要.
在jupyter文档中, 我们用np.mean算出了平均图像:
于是将数据集全部减去这个平均图像, 此外这里我们的图像是行向量, 因此用hstack函数加上1这个元素.得到的shape如下:

SVM的损失函数代码和梯度求解
可以看到, 我们的数据被封为了四个集合, 即训练集, 测试集, 验证集, 开发集. 我们首先利用数量较小的开发集, 来确认我们数学的代码是无误的, 以及测试性能等. 首先assignment给出了允许用循环的代码, 认真阅读就知道这里损失函数就是上面公式的直接翻译. 对于求导, 我们写出L的表达式并征对每个类别的ω分量分别求出表达式计算, 针对每个类别分别求导. 表达式不复杂, 所以也比较好理解.(注意这里仅仅是一个样本的说明,实际上需要相加)

理解了这个代码,也就理解双重循环内部的操作了:
if margin > 0: # max结果不为0
loss += margin # 损失函数加上这项
dW[:, y[i]] += -X[i] # 当前样本序号的结果减去Xi
dW[:, j] += X[i] # 当前计算分量结果加上Xi随后我们这样操作.
loss /= num_train # 求平均损失函数,防止数量过大则dW太大
dW /= num_train
loss += reg * np.sum(W * W) # 正则化项
dW += 2 * reg * W此外jupyter还给出了数值方法求解梯度的方式,这是一种常见的debug的方式,因为我们得到的梯度是一个3073维度的列向量, 所以我们不需要对ωj整个考虑,只需要随机改变ωi某个元素的值,考察梯度变化即可.
ix = tuple([randrange(m) for m in x.shape]) # 随机生成一些idx
oldval = x[ix]
x[ix] = oldval + h # increment by h
fxph = f(x) # evaluate f(x + h)
x[ix] = oldval - h # increment by h
fxmh = f(x) # evaluate f(x - h)
x[ix] = oldval # reset
grad_numerical = (fxph - fxmh) / (2 * h) # 计算双边梯度的近似值可以看到结果相差很小.
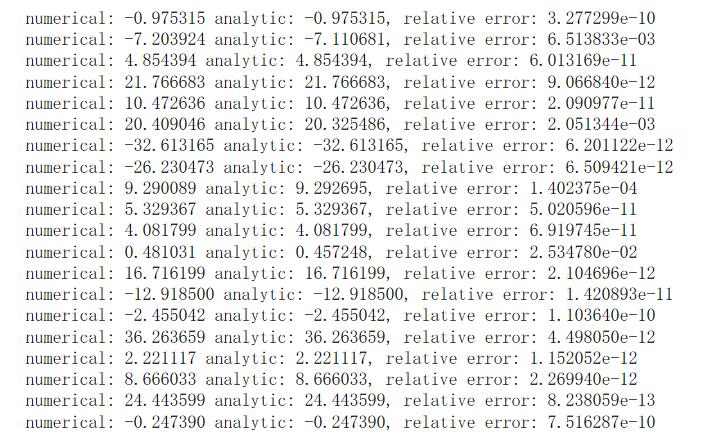
svm_loss_vectorized函数
不过还是和前面一样, 对于大量元素而言, 能用矩阵就不要用循环. 我们知道, 原本的循环就是每个开发集的元素遍历一次是第一层循环, 而在内部对每个分类的loss求和也是一个循环. 实际上求和只需要转化为矩阵的sum就可以了. 我们可以直接通过xω(不是ωx, 虽然ωx也是一种可行选项,但请注意矩阵规模)得到结果为(500,10)的打分, 随后我们的问题是怎么对每一行都通过sum转化成损失. 这里就需要用到numpy强大的切片功能, 切片不仅仅可以对整个区域切片, 还可以对数个区域一次切片. 例如:
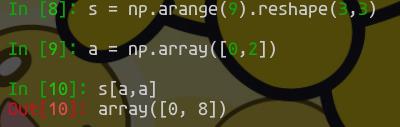
所以, 我们首先需要提取出真实类别的得分,且真实的类别应该设置为0(如果不考虑进去那就是1, 其实不这么做而是整体减去 1*开发集个数 也不是不行). 我们已经知道类别结果存在y内, 为长度500的行向量, 可以直接输入内. 所以我们通过这句话可以完成切片:
real_score = scores[np.arange(num_train), y].reshape(num_train, 1) # arange生成从0-499的数组,而y是类别信息,抽出来就是每个样本的真实类别得分行向量这样, 我们可以利用广播机制直接计算和将真实类别置0:
loss = np.maximum(0, scores - current_score + 1) # 直接广播得到每个的损失
loss[np.arange(num_train), y] = 0 # 对应位置设置为0
loss = np.sum(loss)求解dW: 因为dW的每一列实质上就是加上x向量, 只是有些需要加,有些不需要, 所以还是需要请出内积. 我们思考一下组织形式:
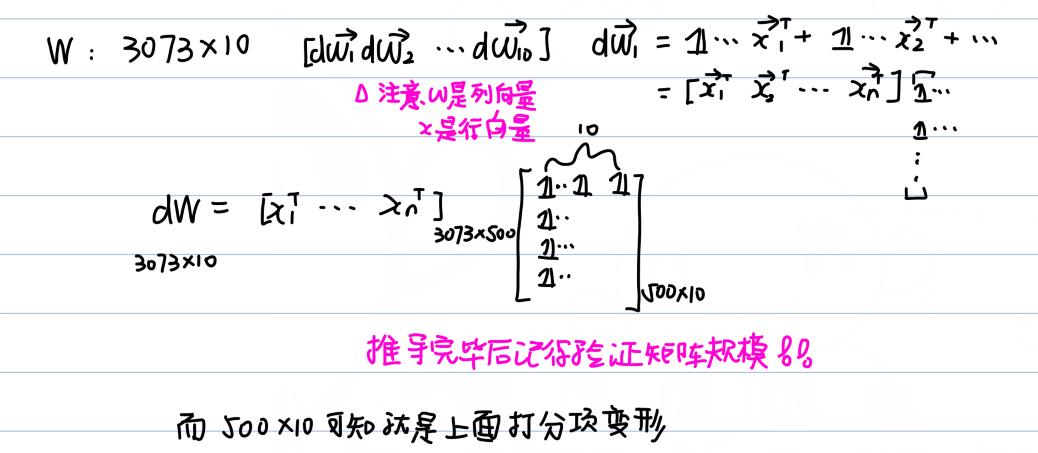
我们知道, 对于其他分类项就是看max符号,符合就是1,否则就是0,而真实项则是统计符合的个数并取负值. 为此, 我们创建一个空500*10矩阵(可以直接用np.zeros_like)函数,毕竟和结果得分规模一致嘛. 我们对需要的地方设置为1, 这是就需要用到np.where函数返回符合条件的索引, 随后设置对应地方为1,对应代码就是:
dW_X = np.zeros_like(scores)
idx = np.where(scores - current_score + 1 > 0)
dW_X[idx] = 1
# 也可以直接dW_X += (scores - current_score + 1 > 0), 因为逻辑矩阵中真为1而按照前面类似方式我们找到需要的符合条件类别的位置:
dW_X[np.arange(num_train), y] = -1 * (np.sum(scores - current_score + 1 > 0, axis=1) - 1) # 注意此时真实类别结果也是1,所以需要减1这样整个代码也就不困难了. 注意别忘了正则化项, 这个和循环版本是完全一致的!
最终效率有高达30倍的差距:
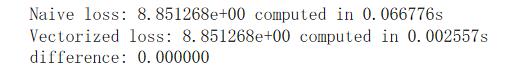
SGD优化器
SGD就是单纯的梯度下降, 也就是我们熟知的 W -= lr * dW的格式. 相比前面真的简单了不少. 注意我们需要随机选择batch_size个元素.
代码如下:
idx = np.random.choice(range(num_train),batch_size,replace=True) # 从0~(num_train-1)选取一些元素,replace表示允许元素重复被选中
X_batch = X[idx,:]
y_batch = y[idx]
# ...
self.W = self.W - learning_rate * grad
# predict函数
scores = X.dot(self.W)
y_pred = np.argmax(scores, axis=1)这样就能开始训练了. 原始训练代码内记录了每次训练的损失.我们可以绘制图像:

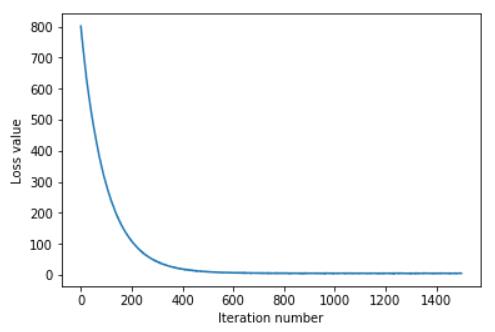
从中可以看出,训练集的loss不断下降, 但是到达750个epoch左右就没有明显下降了,甚至还可能小幅回升, 这时就有可能是过拟合,或者是在最低点附近来回摆动.

最终准确度达到了38%, 相比于KNN的28%左右有了明显进步,但还是很一般.
不同的超参数(lr和reg)
这里只需要对不同的lr和reg组合训练,检查一次正确率就可以. 仍然选取迭代次数为1500:
num_iters = 1500
for lr in learning_rates:
for r in regularization_strengths:
svm = LinearSVM()
loss_hist = svm.train(X_train,y_train,learning_rate=lr,reg=r,num_iters=num_iters,verbose=False) # 关闭输出
y_train_pred = svm.predict(X_train)
acc_train = np.mean(y_train == y_train_pred)
y_val_pred = svm.predict(X_val)
acc_val = np.mean(y_val == y_val_pred)
# 更新准确率
if best_val < acc_val:
best_val = acc_val
best_svm = svm
# 完成记录
results[(lr,r)] = (acc_train,acc_val)
pass默认的lr和reg有种用力过猛的感觉,一下lr这么大,很容易走过头而偏离越来越远,最后远离最优结果,我的评价是:不如瞎猜.

我参考了其他博客的参数选取,得到了这样的结果:

可以看出,在本例下,适当大的lr和较小的reg得到的更好的结果(注意:只是相对),但是没有本质区别.
结果可视化
最终得到的可视化结果和可见上的差不多一致.这里可视化本质上就是将w的每一分类对应重新映射到[0,255]区间内.

问题和解答

回答: 产生严重不匹配的原因是max在0附近的非线性特性,在这种情况下, 就会产生差异

回答: 这个图片的意思就是说, 训练集里面图片多数具备这个形状和颜色, 也就是如果图片像素颜色和模板图像接近, 那么这个类别的打分会比较高.(注意不代表其他类别打分低)
markdown js_cc_01_assignment
以上是关于CS231N assignment 1 _ SVM 学习笔记 & 解析的主要内容,如果未能解决你的问题,请参考以下文章