2023-04-07 无向有权图之最小生成树问题

Posted 2023-04-08 空無一悟

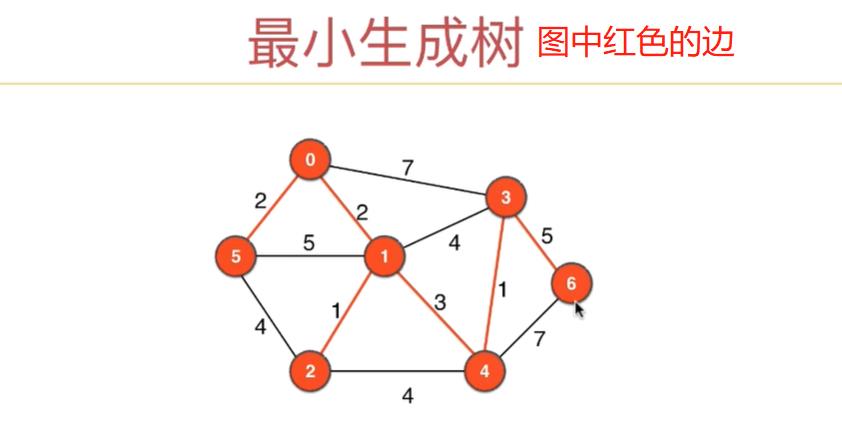
无向有权图之最小生成树问题

前10章我们讲解地都是无向无权图，本章我们将讲解无向有权图，以及无向有权图的经典问题：最小生成树问题(MST:Minimum Spanning Tree)

1~2 无向有权图的实现

主要是用TreeMap代替了无向无权图的TreeSet

本节用到的图

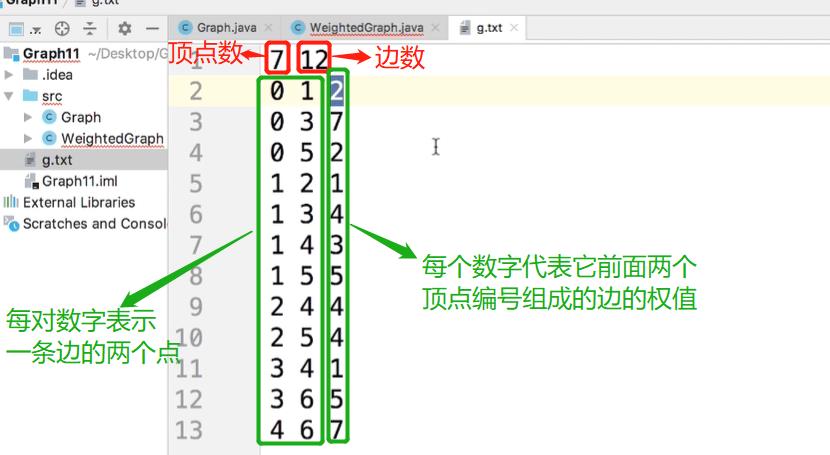
上面的graph.txt对应的图如下：

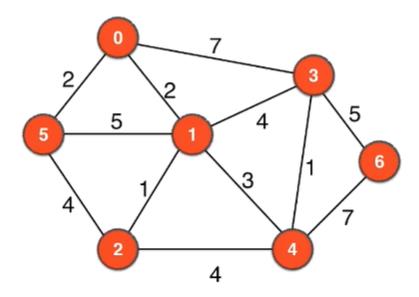
最终的代码

• 无向带权图的基本表示
• 读取无向带权图
• 测试类

3 最小生成树和Kruskal算法

什么是生成树

用n-1条边把含有n个顶点的图连接起来就形成了图的生成树,一个图一般都有很多个不同的生成树

的两个生成树如下：

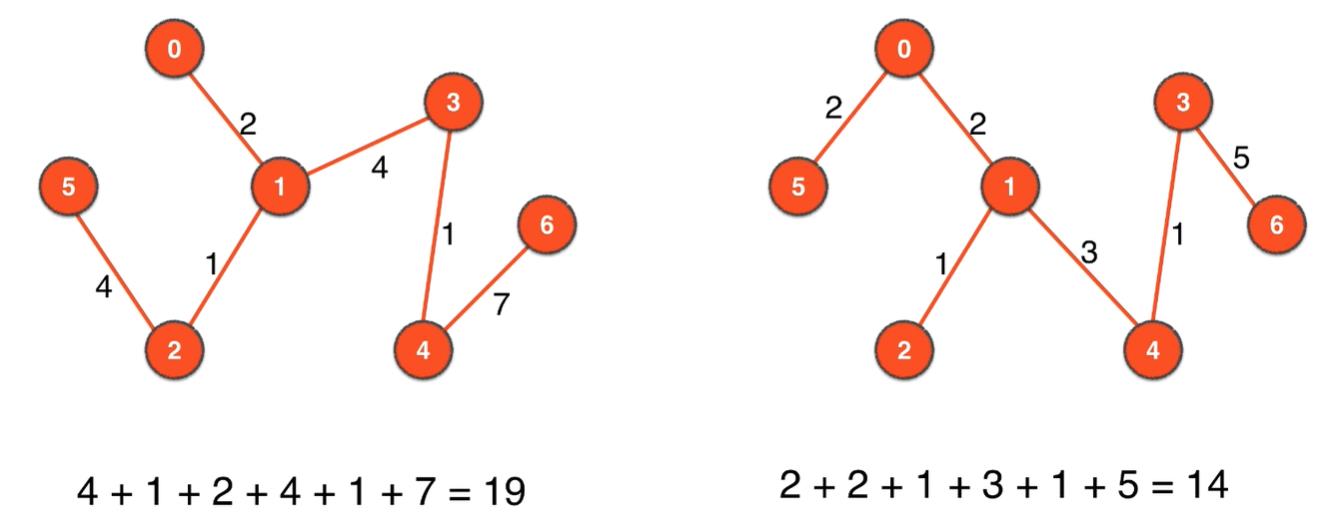
什么是最小生成树

在有权图中，不同的n-1条边形成的不同生成树其权总和一般也就不同，权值总和最小的就叫最小生成树

最小生成树的用途

• 布线设计
• 网络设计
• 电路设计
• 保证图联通且费用最低

求最小生成树的思想

把所有的边进行排序，基于贪心思想使用权值小的边，一旦选到的边使得图中有环就舍弃这条边，如此下去一直到选够n-1条边，这n-1条边组成的生成树就是最小生成树

上面的过程就是求最小生成树的Kruskal算法

4 Kruskal算法正确性的理论保证：切分定理

切分

把图中的顶点分为两部分，就称为一个切分

如下面几个图都不同的颜色均组成一个切分

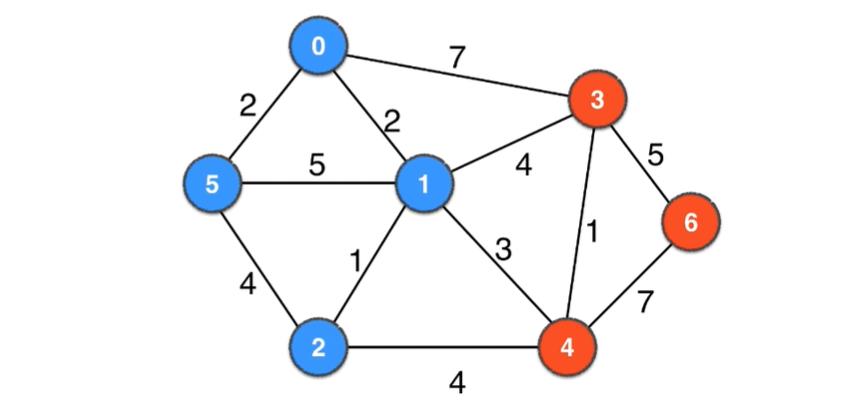
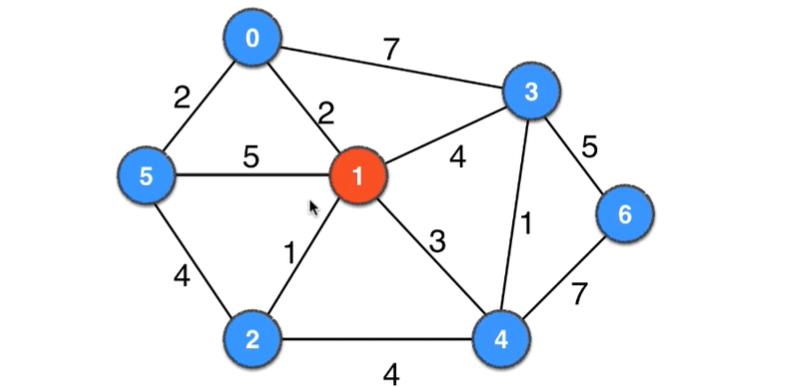
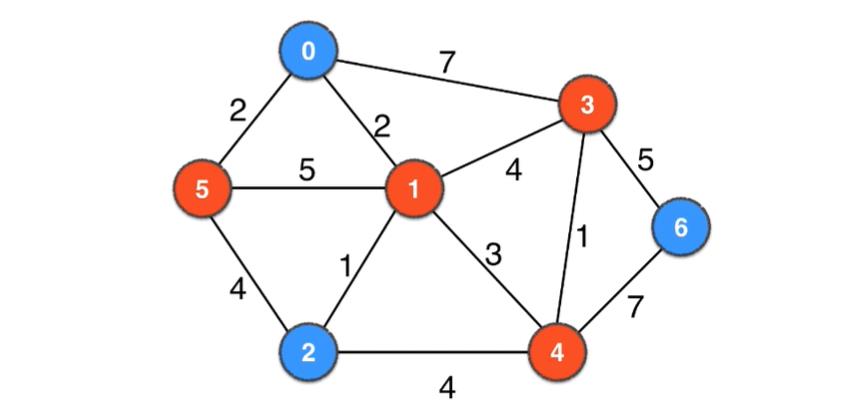
横切边

如果一个边的两个端点，属于切分不同的两边，则这个边被称为横切边

下面是图的一种切分的横切边

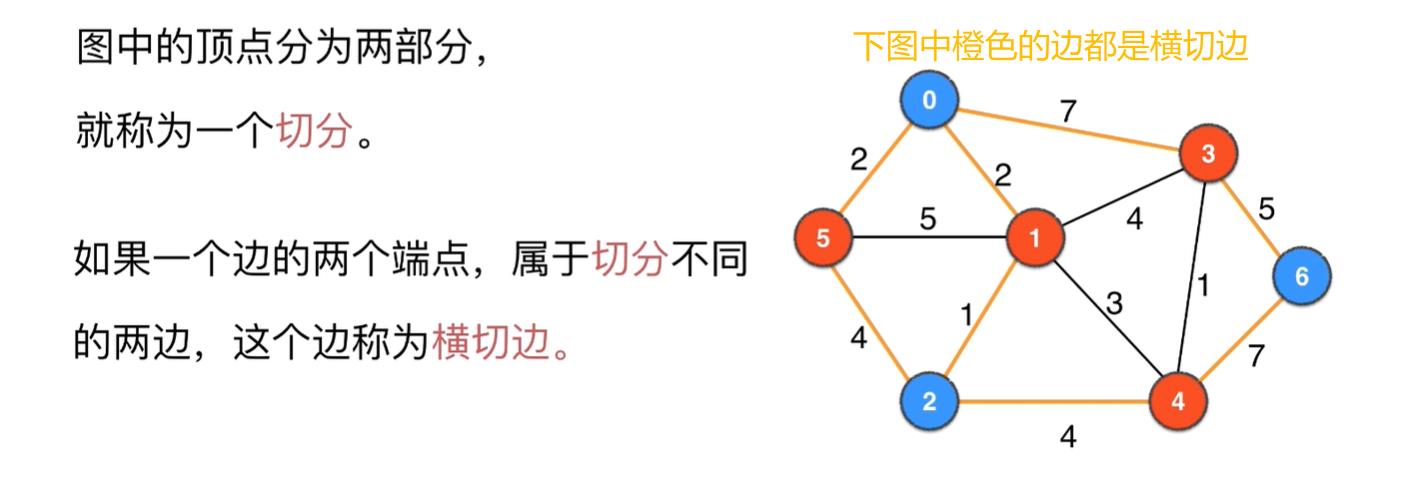
下面是图的另一个切分的横切边：

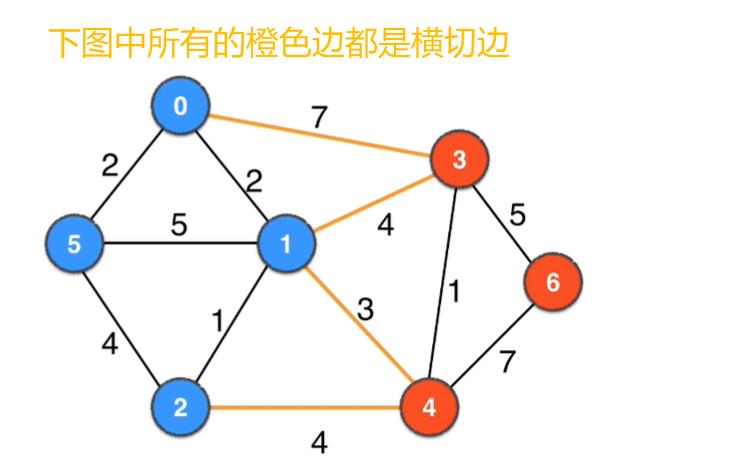
切分定理

横切边中的最短边，一定属于最小生成树

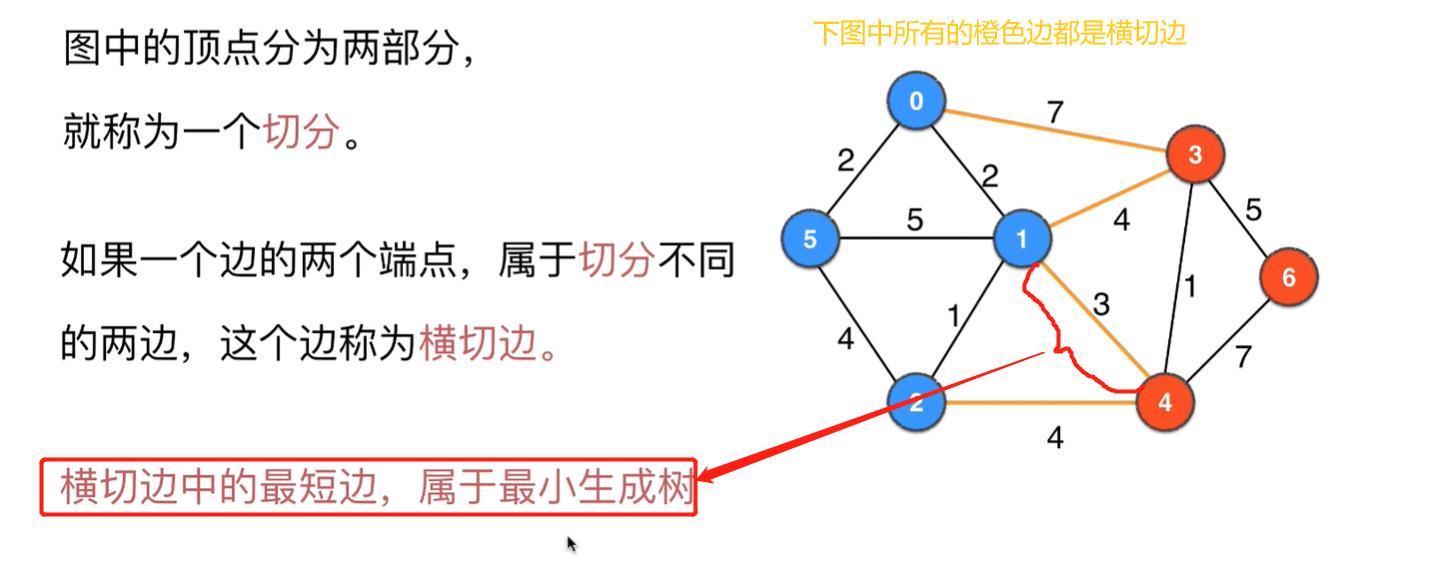
反证法证明：如下图，a、b、c是蓝红切分的所有横切边，红蓝里面的顶点和边加上a组成了最小生成树，a是a、b、c中权值最小的，假设a不是最小生成树的一条边，那么b、c中的一条可以代替a称为最小生成树的一部分(必须从横切边中选取一条才能使得蓝红两部分是联通地)，但是b、c中任何一条加入，新的生成树的权值综合肯定大于替换a之前的，所以得证a一定是最小生成树的一条边

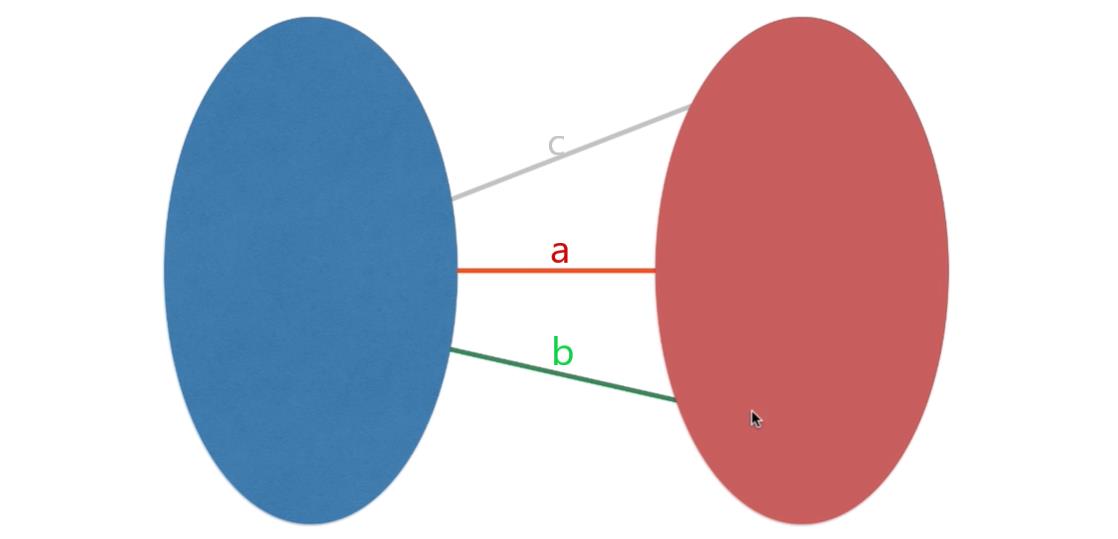
具体的例子可以见下图：

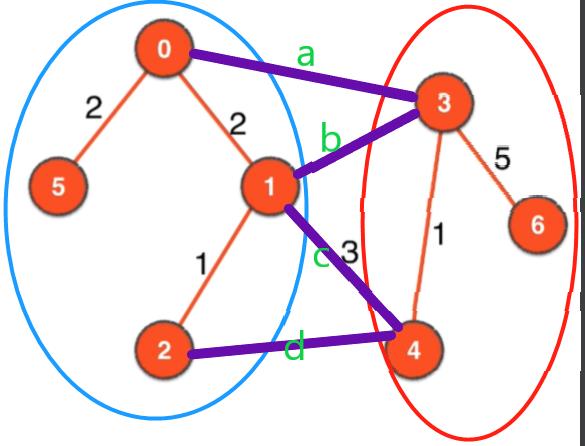
Kruskal算法与切分定理的关系

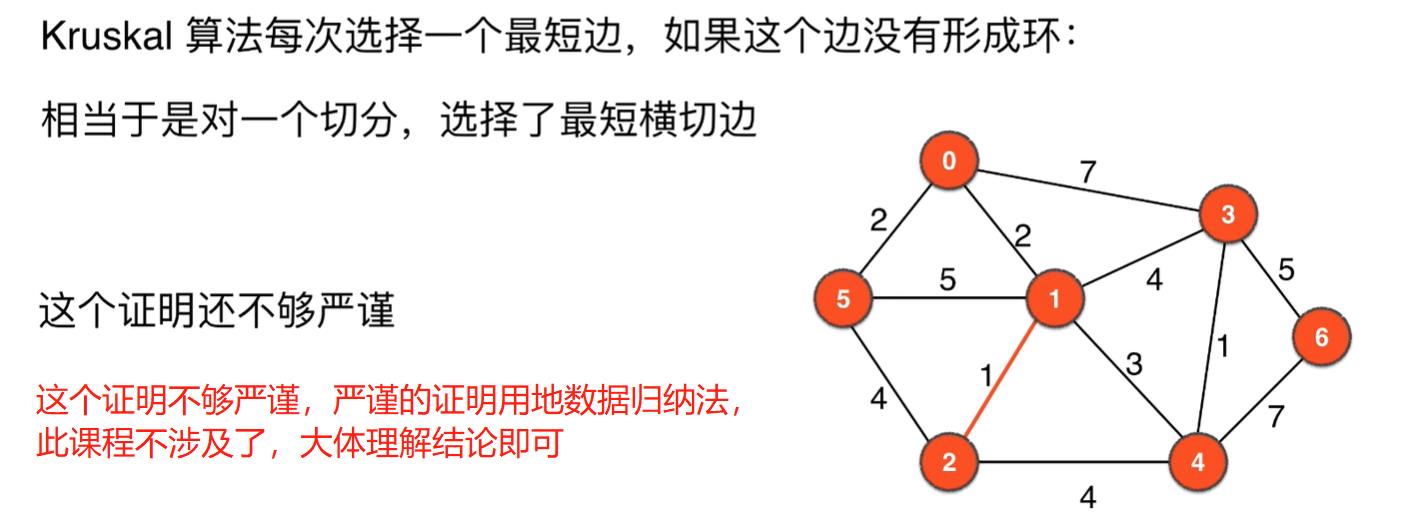
Kruskal算法每次选择一个最短边，如果这个边没有形成环：相当于是对一个切分，选择了最短横切边

5~6 Kruskal算法实现

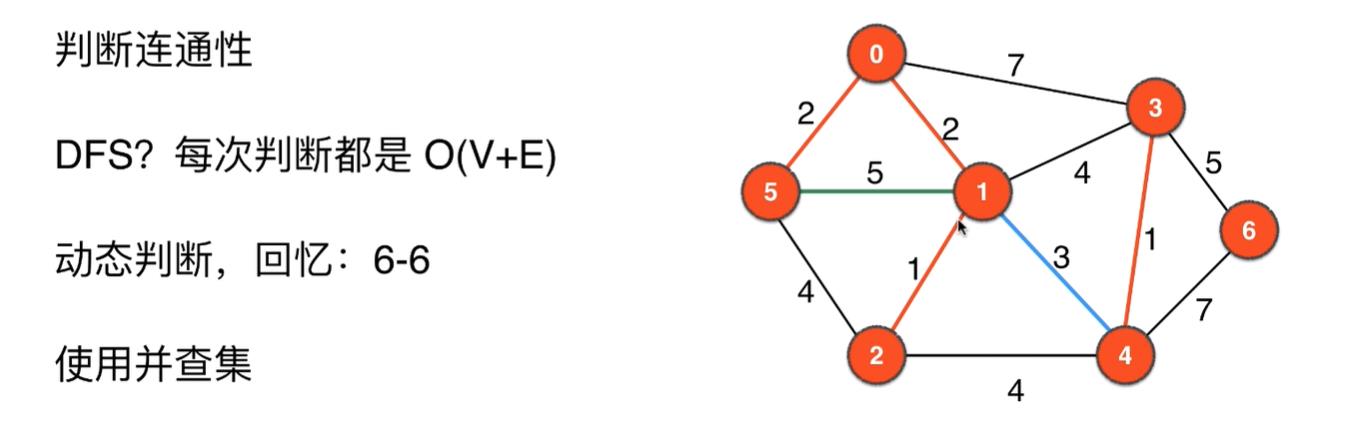
如何快算判断已有的边中是否有环

• DFS 每次判断的事件复杂度都是O(V+E)，而且对动态变化的图性能不高
• 使用并查集：事件复杂度是O(E)，而且支持动态变化的图很好。

所以我们使用并查集来实现已有边中是否有环的快速判断，思想如下：
之前已经加入地边都放到到一个并查集中，一个联通分量内的两个点在并查集中是true，如果我们要加入地边的两个端点在并查集中为true，那么这条边加入一定会生成环。
简而言之，kruskal算法新加入的边的两个顶点在并查集中必须为false，否则不能加入

并查集相关的只是可以参考

• 数据结构精讲Java版 第11章 并查集
• 并查集代码实现参考

Kruskal算法实现

• 算法实现
• 测试代码

测试图如下：

Kruskal求最小生成的时间复杂度是O(ElogE)级别的

时间开销主要是在Collections.sort(edges);上

7~9 Prim算法

回顾切分定理

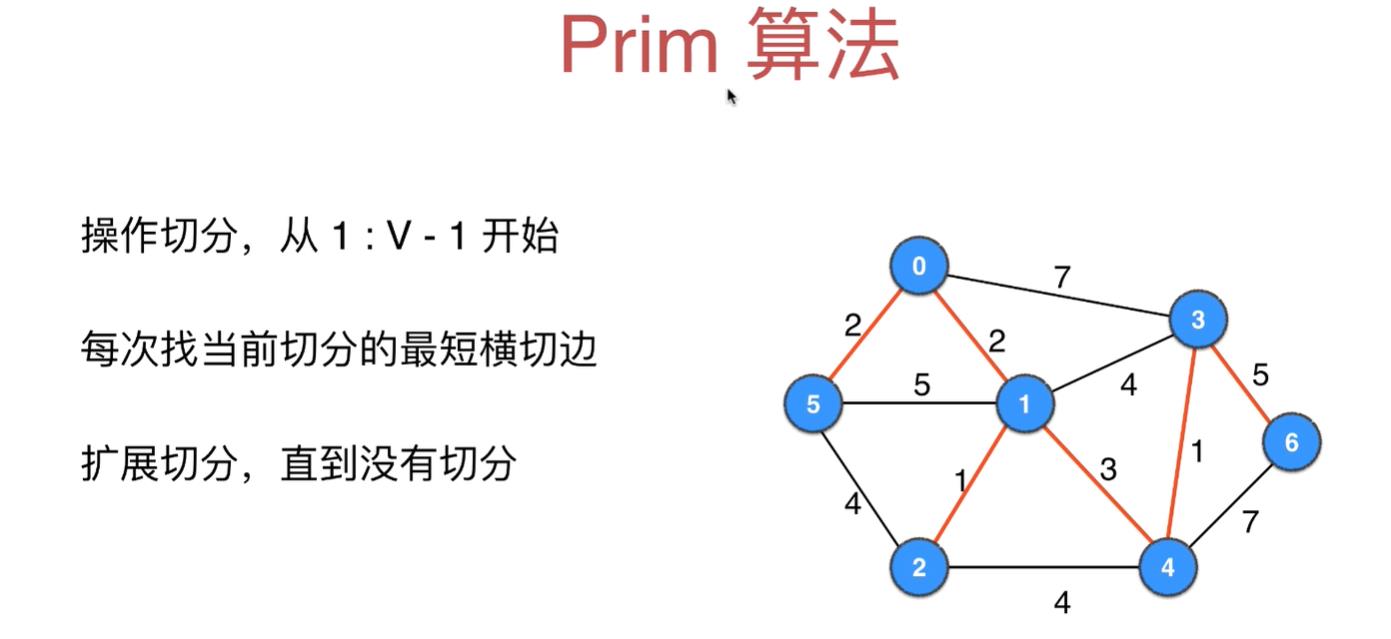
Prim算法的原理和过程模拟

按照顶点个数从(1, v-1)、(2, v-2)、.....不断划分切分，对每种切分都找最短横切边，最后横切边加入到mst列表中，就形成了最小生成树

详细过程模拟如下(@Todo)：

Prim算法的事件复杂度：O(VE)

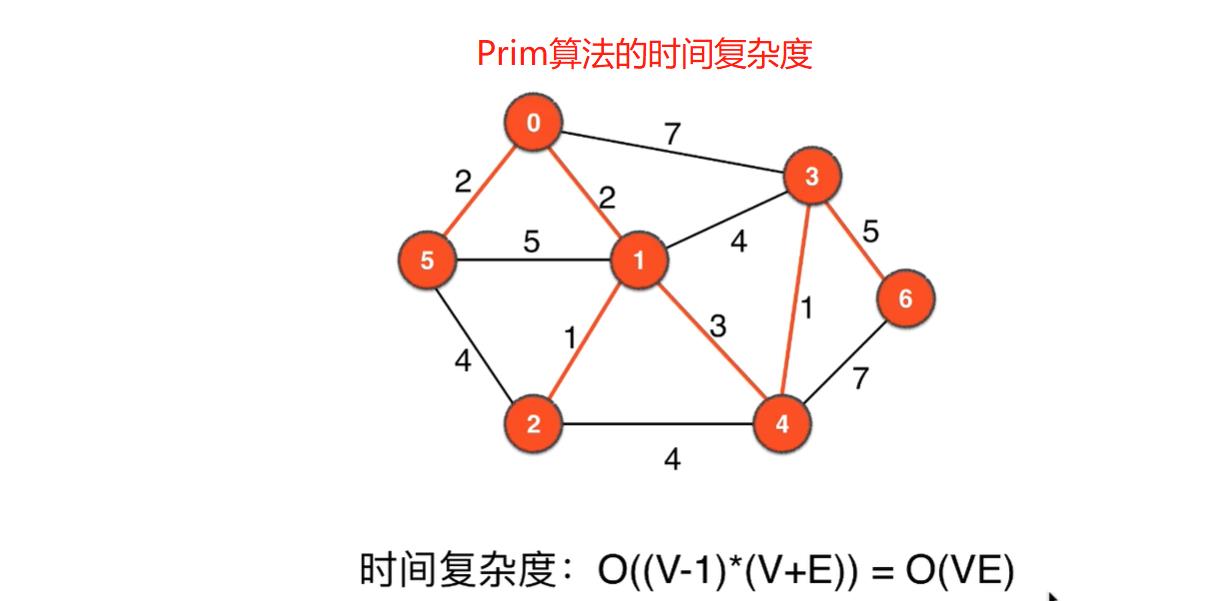
Prim算法优化

基于优先队列(最小堆)快速找到最小的横切边。优化后的算法时间复杂度和Kruskal一样是O(ElogE)

• 未优化的代码
• 优化后的代码
• 测试代码

10 本章总结

知识点

• 带权图
• 最小生成树问题
• 切分定理
• Kruskal求最小生成树
• Prim求最小生成树

Kruskal和Prim算法的代码实现关键

更多最小生成树的算法

给定有权无向图的邻接矩阵如下，求其最小生成树的总权重，代码。

#include<bits/stdc++.h>
using  namespace std;
#define INF 0x3f3f3f3f
const int maxn = 117;
int m[maxn][maxn];
int vis[maxn], low[maxn];
/*
对于这道题目来将，m就是临接矩阵，vis是访问标记数组，low是最短距离数组
*/
int n;
int prim()
{
    vis[1] = 1;
    int sum = 0;
    int pos, minn;
    pos = 1;
    for(int i = 1; i <= n; i++)
    {
        low[i] = m[pos][i];
    }
    /*
    先把第一个点放到树里，然后找到剩下的点到这个点的距离
    */
    for(int i = 1; i < n; i++)//循环遍历 n-1 次数，把点全部加入！
    {
        minn = INF;
        for(int j = 1; j <= n; j++)
        {
            if(!vis[j] && minn > low[j]) //没有进树的节点，并且这个节点到树里面 点距离最近，拉进来
            {
                minn = low[j];
                pos = j;
            }
        }
        sum += minn;
        vis[pos] = 1;
        for(int j = 1; j <= n; j++)
        {
            if(!vis[j] && low[j] > m[pos][j])//用新加入的点，更新low值
            {
                low[j] = m[pos][j];
            }
        }
    }
    return sum;
}
void init()
{
    memset(vis,0,sizeof(vis));
    memset(low,0,sizeof(low));
    for(int i = 1; i <= n ;i++ )
    for(int j = 1; j <= n; j++)
        m[i][j] = INF;
}
void in_map()
{
    printf("输入邻接矩阵阶：\n");
    scanf("%d",&n);
    printf("输入邻接矩阵，无穷用 -1代表！\n");
    int t;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        scanf("%d",&t);
        m[i][j] = (t==-1?INF:t);
    }
}
int main()
{
    init();
    in_map();
    printf("%d",prim());
}