153. 寻找旋转排序数组中的最小值
Posted slowlydance2me
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了153. 寻找旋转排序数组中的最小值相关的知识,希望对你有一定的参考价值。
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
func findMin(nums []int) int left, right := -1, len(nums)-1 // 开区间 (-1, n-1) for left+1 < right // 开区间不为空 mid := left + (right-left)/2 if nums[mid] < nums[len(nums)-1] // 蓝色 right = mid else // 红色 left = mid return nums[right]
本文来自博客园,作者:slowlydance2me,转载请注明原文链接:https://www.cnblogs.com/slowlydance2me/p/17296231.html
二分法08:寻找旋转排序数组中的最小值
寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
思路与算法 : 二分查找
一个不包含重复元素的升序数组在经过旋转之后,可以得到下面可视化的折线图:

在二分查找的每一步中,左边界为 l o w \\it low low,右边界为 h i g h \\it high high,区间的中点为 p i v o t \\it pivot pivot,最小值就在该区间内。我们将中轴元素 nums [ pivot ] \\textit{nums}[\\textit{pivot}] nums[pivot] 与右边界元素 nums [ high ] \\textit{nums}[\\textit{high}] nums[high] 进行比较,可能会有以下的三种情况:
第一种情况是 nums [ pivot ] < nums [ high ] \\textit{nums}[\\textit{pivot}] < \\textit{nums}[\\textit{high}] nums[pivot]<nums[high]。如下图所示,这说明 nums [ pivot ] \\textit{nums}[\\textit{pivot}] nums[pivot] 是最小值右侧的元素,因此我们可以忽略二分查找区间的右半部分。
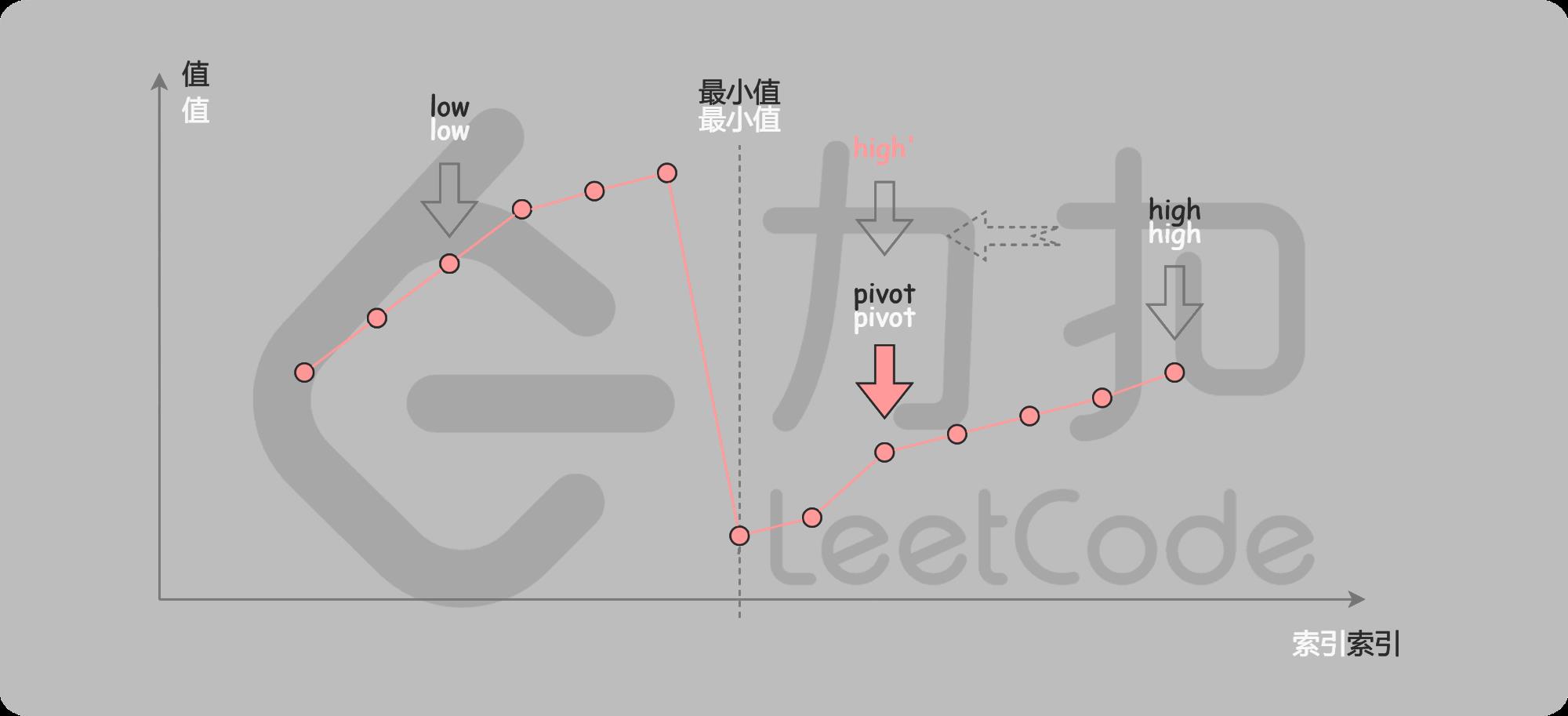
第二种情况是 nums [ pivot ] > nums [ high ] \\textit{nums}[\\textit{pivot}] > \\textit{nums}[\\textit{high}] nums[pivot]>nums[high]。如下图所示,这说明 nums [ pivot ] \\textit{nums}[\\textit{pivot}] nums[pivot] 是最小值左侧的元素,因此我们可以忽略二分查找区间的左半部分。
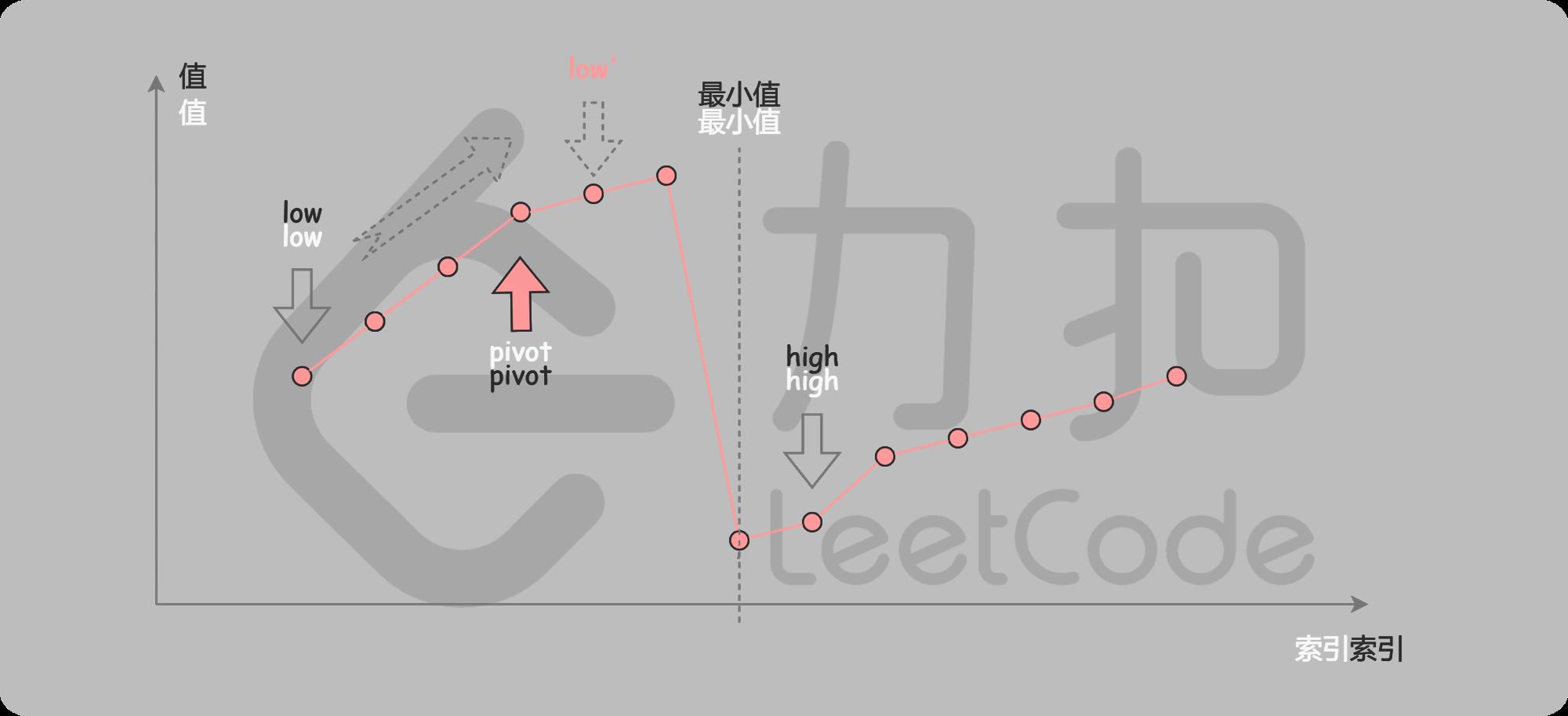
由于数组不包含重复元素,并且只要当前的区间长度不为 1, p i v o t \\it pivot pivot就不会与 h i g h \\it high high 重合;而如果当前的区间长度为 1 ,这说明我们已经可以结束二分查找了。因此不会存在 nums [ pivot ] = nums [ high ] \\textit{nums}[\\textit{pivot}] = \\textit{nums}[\\textit{high}] nums[pivot]=nums[high] 的情况。
当二分查找结束时,我们就得到了最小值所在的位置。
class Solution(object):
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
left = 0; right = len(nums) - 1
while left < right:
mid = left + (right-left) //2
if (nums[mid] < nums[right]): #中值 < 右值,最小值在左半边,收缩右边界
right = mid # 因为中值 < 右值,中值也可能是最小值,右边界只能取到mid处
else: # 中值 > 右值,最小值在右半边,收缩左边界
left = mid+1 # 因为中值 > 右值,中值肯定不是最小值,左边界可以跨过mid
return nums[left] # 循环结束,left == right,最小值输出nums[left]或nums[right]均可
参考
力扣(LeetCode) (leetcode-cn.com)]
《画解剑指 Offer 》
以上是关于153. 寻找旋转排序数组中的最小值的主要内容,如果未能解决你的问题,请参考以下文章