求图的深度优先遍历程序 c语言版
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求图的深度优先遍历程序 c语言版相关的知识,希望对你有一定的参考价值。
求一个图的遍历程序 深度或者广度的都行 要C语言版的 最好附截图 谢谢啊
邻接表表示的图:#include"stdio.h"#include"stdlib.h"#define MaxVertexNum 50 //定义最大顶点数typedef struct node //边表结点
int adjvex; //邻接点域
struct node *next; //链域
EdgeNode;
typedef struct vnode //顶点表结点
char vertex; //顶点域
EdgeNode *firstedge; //边表头指针
VertexNode;
typedef VertexNode AdjList[MaxVertexNum]; //AdjList是邻接表类型
typedef struct
AdjList adjlist; //邻接表
int n,e; //图中当前顶点数和边数
ALGraph; //图类型//=========建立图的邻接表=======
void CreatALGraph(ALGraph *G)
int i,j,k;
char a;
EdgeNode *s; //定义边表结点
printf("Input VertexNum(n) and EdgesNum(e): ");
scanf("%d,%d",&G->n,&G->e); //读入顶点数和边数
fflush(stdin); //清空内存缓冲
printf("Input Vertex string:");
for(i=0;i<G->n;i++) //建立边表
scanf("%c",&a);
G->adjlist[i].vertex=a; //读入顶点信息
G->adjlist[i].firstedge=NULL; //边表置为空表
printf("Input edges,Creat Adjacency List\n");
for(k=0;k<G->e;k++) //建立边表
scanf("%d%d",&i,&j); //读入边(Vi,Vj)的顶点对序号
s=(EdgeNode *)malloc(sizeof(EdgeNode)); //生成边表结点
s->adjvex=j; //邻接点序号为j
s->next=G->adjlist[i].firstedge;
G->adjlist[i].firstedge=s; //将新结点*S插入顶点Vi的边表头部
s=(EdgeNode *)malloc(sizeof(EdgeNode));
s->adjvex=i; //邻接点序号为i
s->next=G->adjlist[j].firstedge;
G->adjlist[j].firstedge=s; //将新结点*S插入顶点Vj的边表头部
//=========定义标志向量,为全局变量=======
typedef enumFALSE,TRUE Boolean;
Boolean visited[MaxVertexNum];
//========DFS:深度优先遍历的递归算法======
void DFSM(ALGraph *G,int i)
//以Vi为出发点对邻接链表表示的图G进行DFS搜索
EdgeNode *p;
printf("%c",G->adjlist[i].vertex); //访问顶点Vi
visited[i]=TRUE; //标记Vi已访问
p=G->adjlist[i].firstedge; //取Vi边表的头指针
while(p) //依次搜索Vi的邻接点Vj,这里j=p->adjvex
if(! visited[p->adjvex]) //若Vj尚未被访问
DFSM(G,p->adjvex); //则以Vj为出发点向纵深搜索
p=p->next; //找Vi的下一个邻接点
void DFS(ALGraph *G)
int i;
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<G->n;i++)
if(!visited[i]) //Vi未访问过
DFSM(G,i); //以Vi为源点开始DFS搜索
//==========BFS:广度优先遍历=========
void BFS(ALGraph *G,int k)
//以Vk为源点对用邻接链表表示的图G进行广度优先搜索
int i,f=0,r=0; EdgeNode *p;
int cq[MaxVertexNum]; //定义FIFO队列
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<=G->n;i++)
cq[i]=-1; //初始化标志向量
printf("%c",G->adjlist[k].vertex); //访问源点Vk
visited[k]=TRUE;
cq[r]=k; //Vk已访问,将其入队。注意,实际上是将其序号入队
while(cq[f]!=-1) // 队列非空则执行
i=cq[f]; f=f+1; //Vi出队
p=G->adjlist[i].firstedge; //取Vi的边表头指针
while(p) //依次搜索Vi的邻接点Vj(令p->adjvex=j)
if(!visited[p->adjvex]) //若Vj未访问过
printf("%c",G->adjlist[p->adjvex].vertex); //访问Vj
visited[p->adjvex]=TRUE;
r=r+1; cq[r]=p->adjvex; //访问过的Vj入队
p=p->next; //找Vi的下一个邻接点
//endwhile
//==========主函数===========
void main()
//int i;
ALGraph *G;
G=(ALGraph *)malloc(sizeof(ALGraph));
CreatALGraph(G);
printf("Print Graph DFS: ");
DFS(G);
printf("\n");
printf("Print Graph BFS: ");
BFS(G,3);
printf("\n");
邻接矩阵表示的图:
#include"stdio.h"
#include"stdlib.h"
#define MaxVertexNum 100 //定义最大顶点数
typedef struct
char vexs[MaxVertexNum]; //顶点表
int edges[MaxVertexNum][MaxVertexNum]; //邻接矩阵,可看作边表
int n,e; //图中的顶点数n和边数e
MGraph; //用邻接矩阵表示的图的类型
//=========建立邻接矩阵=======
void CreatMGraph(MGraph *G)
int i,j,k;
char a;
printf("Input VertexNum(n) and EdgesNum(e): ");
scanf("%d,%d",&G->n,&G->e); //输入顶点数和边数
scanf("%c",&a);
printf("Input Vertex string:");
for(i=0;i<G->n;i++)
scanf("%c",&a);
G->vexs[i]=a; //读入顶点信息,建立顶点表
for(i=0;i<G->n;i++)
for(j=0;j<G->n;j++)
G->edges[i][j]=0; //初始化邻接矩阵
printf("Input edges,Creat Adjacency Matrix\n");
for(k=0;k<G->e;k++) //读入e条边,建立邻接矩阵
scanf("%d%d",&i,&j); //输入边(Vi,Vj)的顶点序号
G->edges[i][j]=1;
G->edges[j][i]=1; //若为无向图,矩阵为对称矩阵;若建立有向图,去掉该条语句
//=========定义标志向量,为全局变量=======
typedef enumFALSE,TRUE Boolean;
Boolean visited[MaxVertexNum];
//========DFS:深度优先遍历的递归算法======
void DFSM(MGraph *G,int i)
//以Vi为出发点对邻接矩阵表示的图G进行DFS搜索,邻接矩阵是0,1矩阵
int j;
printf("%c",G->vexs[i]); //访问顶点Vi
visited[i]=TRUE; //置已访问标志
for(j=0;j<G->n;j++) //依次搜索Vi的邻接点
if(G->edges[i][j]==1 && ! visited[j])
DFSM(G,j); //(Vi,Vj)∈E,且Vj未访问过,故Vj为新出发点
void DFS(MGraph *G)
int i;
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<G->n;i++)
if(!visited[i]) //Vi未访问过
DFSM(G,i); //以Vi为源点开始DFS搜索
//===========BFS:广度优先遍历=======
void BFS(MGraph *G,int k)
//以Vk为源点对用邻接矩阵表示的图G进行广度优先搜索
int i,j,f=0,r=0;
int cq[MaxVertexNum]; //定义队列
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<G->n;i++)
cq[i]=-1; //队列初始化
printf("%c",G->vexs[k]); //访问源点Vk
visited[k]=TRUE;
cq[r]=k; //Vk已访问,将其入队。注意,实际上是将其序号入队
while(cq[f]!=-1) //队非空则执行
i=cq[f]; f=f+1; //Vf出队
for(j=0;j<G->n;j++) //依次Vi的邻接点Vj
if(!visited[j] && G->edges[i][j]==1) //Vj未访问
printf("%c",G->vexs[j]); //访问Vj
visited[j]=TRUE;
r=r+1; cq[r]=j; //访问过Vj入队
//==========main=====
void main()
//int i;
MGraph *G;
G=(MGraph *)malloc(sizeof(MGraph)); //为图G申请内存空间
CreatMGraph(G); //建立邻接矩阵
printf("Print Graph DFS: ");
DFS(G); //深度优先遍历
printf("\n");
printf("Print Graph BFS: ");
BFS(G,3); //以序号为3的顶点开始广度优先遍历
printf("\n");
参考技术A BFS的基本思想是:首先访问初始点v并将其标志为已经访问。接着通过邻接关系将邻接点入队。然后每访问过一个顶点则出队。按照顺序,访问每一个顶点的所有未被访问过的顶点直到所有的顶点均被访问过。广度优先遍历类似与层次遍历。其特点是尽可能先对横向进行搜索,从指定的出发点,按照该点的路径长度由短到长的顺序访问图中各顶点。下面给出bfs函数代码:void bfs(Graph *g,int vi)
int i,v;
int Q[max],front=0,rear=0;//循环队列
Edgenode *p;
for(i=0;i<g->n;i++)
visited[i]=0; //队列赋初值
visited[vi]=1; //访问初始顶点
printf("--%c--",g->v[vi].c);
rear=(rear+1)% max;
Q[rear]=vi;//初始顶点入队列
while(front!=rear) //队列不为空的时候循环
front=(front+1)%max;
v=Q[front]; //出队列
p=g->v[v].first;//查找v的第一个邻接点
while(p!=NULL)//查找v的所有邻接点
if(visited[p->b]==0)//未访问过则访问之
visited[p->b]=1;
printf("--%c--",g->v[p->b].c);//访问该点并入队
rear=(rear+1)%max;
Q[rear]=p->b;
p=p->next; //查找v的下一邻接点
请仔细理解其中队列的使用。 完整程序:#include<stdio.h>
#define max 6
typedef struct node
int b;
struct node* next;
adjnode; //定义边表节点
typedef struct vertex
int c;
adjnode *first;
vertexnode; //定义顶点
typedef struct graph
vertexnode v[max];
int vertex,edge;
adjgraph; //定义图的结构
int visited[max];
void creatg(adjgraph *g) //初始化创建图
int i,j,e,f;
adjnode *p,*q;
for(i=0;i<5;i++) //这里的4就是vertex的值可以用g->vertex换过来
g->v[i].c=getchar(); g->v[i].first=NULL; //图的顶点赋值这里就是赋的0123
for(j=0;j<5;j++) //这里的5就是edge的值也可换
printf("Please input 邻接边:\n");
scanf("\n%d,%d",&e,&f); //输入邻接边
p=(adjnode *)malloc(sizeof(adjnode));
p->b=f;
p->next=g->v[e].first; //插入领接边的表是从中间插着接的。注意了!
g->v[e].first=p; //注意这两个指针的使用。比较巧妙
q=(adjnode *)malloc(sizeof(adjnode)); //一个图只要输入相应的边即可
q->b=e; //这两个接点将两个顶点的邻接表
q->next=g->v[f].first; //的节点都接上了。注意体会
g->v[f].first=q;
void dispg(adjgraph *g) //输出图,打印出邻接表
int i,j;
adjnode *p;
for(i=0;i<4;i++) //打印4个节点的情况
printf("%c",g->v[i].c);
p=g->v[i].first;
while(p!=NULL)
printf("->%d",p->b);<br> p=p->next;
printf("\n");
void bfs(adjgraph *g,int vi)
int i,v;
int Q[max],front=0,rear=0;//循环队列
adjnode *p;
for(i=0;i<g->vertex;i++)
visited[i]=0; //队列赋初值
visited[vi]=1; //访问初始顶点
printf("--%c--",g->v[vi].c);
rear=(rear+1)% max;
Q[rear]=vi;//初始顶点入队列
while(front!=rear) //队列不为空的时候循环
front=(front+1)%max;
v=Q[front]; //出队列
p=g->v[v].first;//查找v的第一个邻接点
while(p!=NULL)//查找v的所有邻接点
if(visited[p->b]==0)//未访问过则访问之
visited[p->b]=1;
printf("--%c--",g->v[p->b].c);//访问该点并入队
rear=(rear+1)%max;
Q[rear]=p->b;
p=p->next; //查找v的下一邻接点
int main()
adjgraph *g;
g=(adjgraph *)malloc(sizeof(adjgraph));
creatg(g);
dispg(g);
bfs(g,0);
system("pause");
参考技术B #include "stdio.h"
#include "malloc.h"
#define MAX 20int visited[MAX];typedef struct ArcNode
int adjvex;
struct ArcNode *nextarc;
ArcNode;typedef int Vertex;typedef struct VNode
Vertex data;
struct ArcNode *firstarc;
VNode;typedef VNode AdjList[MAX];typedef struct
AdjList adjlist;
int vexnum,arcnum;
ALGraph; CreateDG(ALGraph *G) /*创建邻接表*/
int i,k,j,v1,v2;
ArcNode *p;
printf("shu ru tu de ding dian shu ,hu du:" );
scanf("%d,%d",&G->vexnum,&G->arcnum);
printf("\n");
for(i=0;i<G->vexnum;++i)
G->adjlist[i].firstarc=NULL;
for(k=0;k<G->arcnum;++k)
printf("shu ru di%dtiao de hu wei he hu tou:",k);
scanf("%d,%d",&v1,&v2);
i=v1;j=v2;
p=(ArcNode *)malloc(sizeof(ArcNode));
p->adjvex=j;
p->nextarc=G->adjlist[i].firstarc;
G->adjlist[i].firstarc=p;
DispAdj(ALGraph *G) /*输出邻接表*/
int i;
ArcNode *q;
for(i=0;i<G->vexnum;++i)
q=G->adjlist[i].firstarc;
printf("%d",i);
while(q!=NULL)
printf("->%d",q->adjvex);
q=q->nextarc;
printf("\n");
DFS(ALGraph *G,int v) /*深度优先搜索周游*/
ArcNode *p;
visited[v]=1;
printf("%d ",v);
for(p=G->adjlist[v].firstarc;p!=NULL;)
if(!visited[p->adjvex])
DFS(G,p->adjvex);
p=p->nextarc;
BFS(ALGraph *G,int v) /*广度优先搜索周游*/
int queue[MAX],front=0,rear=0;
int w,i;
ArcNode *u;
for(i=0;i<G->vexnum;++i) visited[i]=0;
visited[v]=1;
printf("%d ",v);
rear=(rear+1)%MAX;
queue[rear]=v;
while(front!=rear)
front=(front+1)%MAX;
w=queue[front];
for(u=G->adjlist[w].firstarc;u!=NULL;)
if(!visited[u->adjvex])
visited[u->adjvex]=1;
printf("%d ",u->adjvex);
rear=(rear+1)%MAX;
queue[rear]=u->adjvex;
u=u->nextarc;
printf("\n");
main() /*主函数*/
int i,j,k;
ALGraph *G;
printf("\n");
G=(ALGraph *)malloc(sizeof(ALGraph));
CreateDG(G);
printf("tu de ling jie biao wei:\n");
DispAdj(G);
printf("\n");
printf("cong ding dian 0 kai shi de shen du sou suo:\n");
DFS(G,0);
printf("\n");
printf("cong ding dian 0 kai shi de guangdu du sou suo:\n");
BFS(G,0);
printf("\n");
getch();
超详细C语言版数据结构:图的深度优先遍历(推荐收藏)
文章目录
一、邻接矩阵存储图的深度优先遍历过程分析
对图1这样的无向图,要写成邻接矩阵,则就是下面的式子:

一般要计算这样的问题,画成表格来处理是相当方便的事情,实际中计算机处理问题,也根本不知道所谓矩阵是什么,所以画成表格很容易帮助我们完成后面的编程任务。在我们前面介绍的内容中,有不少是借助着表格完成计算任务的,如Huffman树。
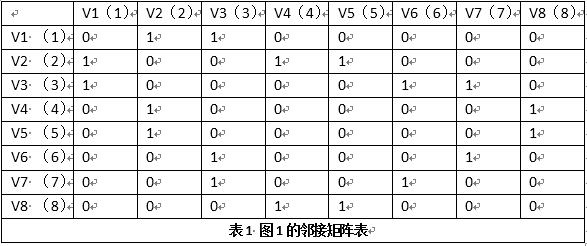
为了记录那些顶点是已经走过的,还要设计一个表来标记已经走过的顶点,在开始,我们假设未走过的是0,走过的是1,于是有:

深度优先遍历过程如下:
(1)从第1行开始,寻找和V1相连的第1个顶点,首先在Visited表中标记V1被访问到,就是:

在该行,我们找到的第一个连接顶点是V2,找到V2顶点后,记录:V1->V2,意味着我们已经抵达V2,注意修改邻接矩阵表;

(2)然后则转向V2顶点所在的行,意味着我们已经抵达V2,再次在Visited表中标记V2顶点已经被访问,就是:

然后,寻找连接V2的、并且是未被访问过的第一个顶点,就是V4:记录V2->V4;

(3)然后则转向V4顶点所在的行,意味着我们已经抵达V4,再次在Visited表中标记V4顶点已经被访问,就是:

然后则转向V4顶点所在的行,寻找连接V4的、并且是未被访问过的第一个顶点,就是V8:记录V4->V8;

(4)然后则转向V8顶点所在的行,意味着我们已经抵达V8,再次在Visited表中标记V8顶点已经被访问,就是:

然后则转向V8顶点所在的行,寻找连接V8的、并且是未被访问过的第一个顶点,就是V5:记录V8->V5;

(5)然后则转向V5顶点所在的行,意味着我们已经抵达V5,再次在Visited表中标记V5顶点已经被访问,就是:

寻找连接V5的、并且是未被访问过的第一个顶点,此处未找到,注意V2、V8顶点已经在Visited表中标记已访问过。

(5)这个地方一定注意:V5上找不到未访问过的顶点,说明此路到此就算走死了。
此时看Visited表:其中还有顶点没有抵达过,于是要按原路返回,所谓原路就是从表12、表10、表9走过的路线返回、然后逐个查找这些顶点上有无未抵达过的顶点。过程如下:再次从V5返回到V8,查找V8上有无未抵达过的顶点,结果是无;
再次从V8返回到V4,查找V4上有无未抵达过的顶点,结果是无;
再次从V4返回到V2,查找V2上有无未抵达过的顶点,结果是无;
再次从V2返回到V1,查找V1上有无未抵达的顶点,结果是V3,于是重复第(1)步,首先标记V3访问到:
标记V1->V3,标记Visited表V3被访问:

到V3,就是这样的情况:

(6)到达V3后,寻找第一个未被访问过的顶点:V6,首先标记Visited表,说明已经抵达V6,就是:

再从V6开始找下一个顶点就是V7:
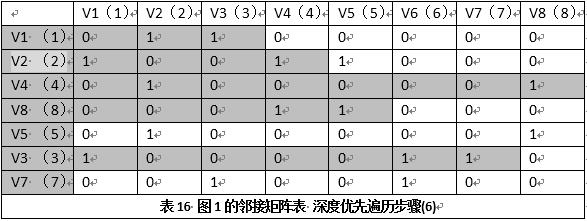
(7)在Visited表中标注V7已经访问到,就是:

至此,图1的深度优先遍历完成。
二、结果分析
从上面的过程可以看出:仅仅就顶点访问到的次序而言,图1的深度优先遍历结果是:
V1->V2->V4->V8->V5->V3->6->V7
但实际执行过程中我们可以发现:所谓图的遍历、其结果应该是一个树:

在C语言中,显示这个结果并不容易,所以大多教材中并不会给出这样的结果。
三、C语言编程实现图的深度优先遍历
图1只有8个顶点,可在实际中,一个图的顶点个数是不确定的,在编程中要保存顶点数据、邻接矩阵,首先就要考虑动态数组;其次,为了方便邻接矩阵的输入和修改,最好是把数据保存在文本文件中。在我们的教材中、程序使用了键盘输入的方式,而在实际操作中、在图的顶点个数比较多的情况下,手工无差错输入很多数据、几乎是无法办到的事情,为此,我们在文件p176G719.txt中保存了图1的邻接矩阵数据。这个文件的名称含义是:教材176页图7.19的顶点名称和邻接矩阵数据。有了这样的数据文件,在记事本程序中可以很方便的修改和补充数据。这个文件的内容如下:
8
V1
V2
V3
V4
V5
V6
V7
V8
0 1 1 0 0 0 0 0
1 0 0 1 1 0 0 0
1 0 0 0 0 1 1 0
0 1 0 0 0 0 0 1
0 1 0 0 0 0 0 1
0 0 1 0 0 0 1 0
0 0 1 0 0 1 0 0
0 0 0 1 1 0 0 0
这个文件第一行是8,说明这个图有8个顶点,随后在第2行到第9行,则是图的顶点名称,第10行到末尾,则是该图的邻接矩阵。
根据不同的图,在记事本程序中完成这样的数据是非常简单的事情,哪怕错了再修改也是很容易做到。
1 设计图的存储结构以及数据文件读取
图的存储、无论哪种方法,都是由两部分组成的,一个是顶点名称集合,一个是顶点关系集合,在邻接矩阵方式中,顶点名称是一个字符串数组,而顶点关系则是一个矩阵、这个矩阵在C语言中是一个二维数组。于是图的结构可以是:
struct Graph
int A[100][100]; //邻接矩阵
char V[100][20]; //顶点名称矩阵,100行,每个名称字符串不超过20字节
int num; //顶点个数
int Visited[100]; //访问记录表
;
但这样的定义很死板,它假设程序最大是100个顶点,实际我们的教材中就是这么定义的。但幸好我们前面已经知道该怎么处理二维数组,于是这里我们可以动态申请内存,以保证在很多顶点的情况也能使用,对二维数组,则上述定义变为:
struct Graph
int **pA; //邻接矩阵指针
char **pV; //顶点名称指针
int num; //顶点个数
int *Visited;//访问记录表指针
;
对这样数组的构造,参见第5部分:数组,好在我们前面有过介绍。
回忆一下,如有数组:
int A[3][3]=1,2,3,4,5,6,7,8,9;
则A[0]、A[1]、A[2]则代表每一行的地址,一般称为行首地址,比如这三行行首地址分别是[100]、[200]、[300],这三个地址数据分别存储在地址[2000]、[2001]、[2002]的存储空间里,则地址[2000]就是这个数组A的含义,就是所谓行首地址数组的首地址。
反过来,如:
int *p[3];
p[0]=A[0];p[1]=A[1];p[2]=A[2];
上面的式子里,如p[0]地址为[3000]、[3001]、[3002],其中的内容保存的是100、200、300,这样就相当于保存了A数组的行首地址,所以p就是个二维数组行首指针数组,只不过它仅仅是三行的二维数组。如把p[0]的地址给另外一个指针变量pA,则pA就是:
int **pA;
假如这个变量的地址在[5000],给这个变量赋值:
pA=&p[0];
于是地址[5000]中将存储3000,这里pA和A的含义是一致的。实际数组A本身就是地址[5000],如有以下语句:
X=A[1][2];
就是从A的地址[5000] 、读到内容3000、再从3001读到200、再从200后取第1个数,过程如下图3所示:

针对n个顶点,则初始化一个图的函数就是:
#define VLENGTH 20 //定义每个顶点名称不超过20字节
struct Graph *GraphInit(int n)
int i;
struct Graph *g;
if(n<=0) return NULL;
g=(struct Graph *)malloc(sizeof(struct Graph));
g->num=n;
g->pA=(int **)malloc(sizeof(int )*n);
g->pV=(char **)malloc(sizeof(char)*n);
for(i=0;i<n;i++)
g->pA[i]=(int *)malloc(sizeof(int)*n);
g->pV[i]=(char *)malloc(sizeof(char)*VLENGTH);
g->Visited=(int *)malloc(sizeof(int )*n);
for(i=0;i<n;i++)
g->Visited[i]=0;
return g;
注意第9行,是为行首地址数组申请内存;
注意第13行,是为每行数据申请存储空间;
注意第14行,前面定义每个顶点的名称是VLENGTH长度,这里是20字节。
由于C语言的指针可以用下标法读写内容,所以完全可以把pA、pV当做普通的二维数组来处理,此处不再叙述。
2 从文件中读数据到邻接矩阵和顶点名称矩阵
这个过程在链表的处理中已经介绍过了,只不过数据格式有差异而已。针对我们前面介绍的数据格式,读数据文件并构造图的函数如下:
struct Graph * GraphCreat(char FileName[20])
int i,j,n;
FILE *fp,*fopen();
struct Graph *G;
fp=fopen(FileName,"r");
if(fp==NULL) return NULL;
fscanf(fp,"%d",&n);
G=GraphInit(n);
for(i=0;i<n;i++)
fscanf(fp,"%s",G->pV[i]);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
fscanf(fp,"%d",&G->pA[i][j]);
fclose(fp);
return G;
第8行首先读文件中顶点个数,然后根据顶点个数、使用GraphInit()申请内存并构造这个图的存储空间,然后在第10行读n个顶点名称、在第12行按二维数组的组织读邻接矩阵。最后,返回G就是包含有顶点名称、邻接矩阵的图的存储空间。
有了这两个函数后,就可以编写main()来测试它们,就是:
main()
int i,j;
struct Graph *G;
G=GraphCreat("p176G719.txt");
//打印顶点名称
for(i=0;i<G->num;i++)
printf("%s ",G->pV[i]);
printf("\\n");
//打印邻接矩阵
for(i=0;i<G->num;i++)
for(j=0;j<G->num;j++)
printf("%d ",G->pA[i][j]);
printf("\\n");
这个程序第5行,你可以修改成用scanf()来读到一个文件名称字符串,然后,就可以使用任何格式符合要求的数据文件了。
G0.C中还包含有GraphFirstAdj()、GraphNextAdj()、GraphDestory()三个函数,这些函数的意义你能看懂么?
2 深度优先遍历的编程实现
从前面算法分析过程可知:对一个图的深度优先遍历,实际就是从第n个顶点开始、标记该顶点已被访问,然后查找该顶点上第一个和它相连、并且未被访问到的顶点、比如是第i个顶点,再去第i个顶点,如此繁琐的说这些,实际就是:
void DFS(struct Graph *G,int n)
int i;
if(G==NULL) return;
if(n<0||n>G->num) return;
G->Visited[n]=1;
printf("%s ",G->pV[n]);
for(i=0;i<G->num;i++)
if(G->pA[n][i]!=0&&G->Visited[i]!=1) DFS(G,i);
第6行是标记该顶点被访问;
第9行就是:查找第n个顶点上、未被访问到的顶点,如找到该顶点、且顶点编号是i,则再次DSF(G,i);
有了这个函数后,构造main()开始从第0个顶点遍历图1,就是:
main()
int i,j;
struct Graph *G;
G=GraphCreat("p176G719.txt");
for(i=0;i<G->num;i++)
printf("%s ",G->pV[i]);
printf("\\n");
for(i=0;i<G->num;i++)
for(j=0;j<G->num;j++)
printf("%d ",G->pA[i][j]);
printf("\\n");
DFS(G,0);
printf("\\n");
进一步测试该函数,按图1的数据仔细分析下它的执行过程,如有图的连接分量不为1,则会在第一个连接分量遍历完成后终止。如下图4,在G1.C中是无法全部遍历完成的。这个图的文件在G4.TXT,修改表23中第5行,从G4.TXT中读数据,则会发现这个程序仅仅遍历了A、B、C、D,而没有到达过E、F、G这三个顶点。

为确保多个分量的图都能顺利遍历完成,则该函数退出后还需要判断是有顶点是否确保全部遍历完成、并确保每次遍历开始的时候、其访问数组Visited[]中全部是0,就是:
void DFSTraverse(struct Graph *G)
int i;
if(G==NULL) return;
for(i=0;i<G->num;i++)
G->Visited[i]=0;
for(i=0;i<G->num;i++)
if(G->Visited[i]==0) DFS(G,i);
表24中函数,很容易修改成计算图的连接分量的函数,这个工作就由同学们自己完成。如果你遇到困难无法完成,参见G3.C
略加修改main()函数,补充:
DFSTraverse(G);
即可完成图4的深度优先遍历。到此,C语言的深度优先遍历到此结束。
四、图的遍历及其应用
1 图的关节点
图的关节点、在图上或许仅仅是个理论或者方法,但对GIS而言,却绝对是个重要意义的理论、尽管目前还没见到这类应用。
求解图的关节点、是典型的深度优先遍历应用,首先我们从教材中找到G5的图,其邻接矩阵如下:

从A点开始、进入A点后由邻接矩阵右端向左遍历,其结果就是:ALMJBHKGIDECF
仔细根据上述结果、可以得到图5这样的深度遍历生成树。
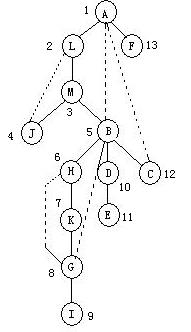
注意图5:每个结点上标注的数字是在深度优先遍历上抵达的次序。
对这个邻接矩阵,我们从右向左做了深度优先遍历,这代表着一个方向,然后,我们要从左到右、在遍历的时候、逐个结点寻找与当前结点相连的最小次序结点(这里一直没想好个比较恰当的措辞来描述这个概念),而这个结点、则构成了所谓的回边路径,如图5中虚线所指的线路,如J-L、B-A等线路。这种线路很关键:它的物理意义是:你可以通过B直接抵达A、或者C直接抵达A、G直接抵达B等等,这些回边路径,则立刻喻示着你炸毁K点、对I点则没什么影响。
从右向左深度优先遍历,这里的现实意义就是说:从其他各个顶点回到A的情况。
相连最小次序结点序号,通常用Low[ ]数组来表示,比如J结点,这个值就是2,它代表着J可以抵达第2个遍历到的结点L,这就是所谓的回边路径。同理,对于C,这个值是1,它代表着在C点,可以直接到A。
如果当前结点下标是v,而在Visited[v]代表这个结点深度遍历中的次序,w代表v顶点在生成树上的孩子结点下标,k代表v的祖先结点下标,则:
Low[v]=minVisited[v],Low[w],Visited[k]
当然,这个式子很简洁,要真正计算出来Low[ ]的值、显然要在程序上说了算。而要在编程中体现这些,还要首先是能手工计算出这个值来。
2 关节点的计算
首先我们设计表格如下:

(1) 顶点A,步骤1
对于A,它就是来自步骤1,就是A,于是Low为1。
(2) 顶点L,步骤2
现在,根据遍历的次序,我们抵达L这个顶点,注意L的邻接矩阵:

从表27可知:深度优先遍历经过的顶点里有A、J、M,其中只有A是深度优先遍历访问过的顶点、所以最小次序号是1,也就是A是L能直接抵达的回边路径上的顶点,所以,表26就是以下结果:


(3) 顶点M,步骤3
现在,我们根据表28抵达顶点M,这个顶点的邻接矩阵表如下:

这个地方可以看到:M可以和B、J、L相连,但B、J尚未被访问过,而M又从L而来,所以此时M的回边就是L的回边,于是有:

(4) 顶点J,步骤4
根据遍历的次序,我们进入顶点J,此时邻接矩阵如下:

对于顶点J,这里可知与L、M相连,从表30知道L是步骤2到达、M是步骤3到达,取步骤次序最小、即为2,它意味着在顶点J上可以抵达深度遍历次序为2的顶点、就是L,于是有:

从这个表第4步,我们回头看图5,就相当于J与L之间的连接虚线。在L、M之间找最小连接次序的意义是:把M炸掉、J依然能回到L。
(5) 顶点B,步骤5
依然要看邻接矩阵,B顶点是:

在这里,我们发现B与A、C、D、G、H、M相连,其中:A、M是深度优先遍历已经遍历过得顶点,找最小次序的、就是A,也就是第一步就抵达的顶点,所以有:

(6) 顶点H,步骤6
再次看邻接矩阵表,H顶点就是:

可以发现H与B、G、K连接,其中B是深度优先遍历访问过的顶点,注意到B的是在第5步访问的,所以有:

对于顶点H,该顶点是由邻接矩阵这种硬性连接造成的回边路径只能是5、就是说它只能通过B回到A,这就非常麻烦,立刻喻示着B是一个关节点。
(7) 顶点K,步骤7
同样要仔细看邻接矩阵,K就是:

我们看到K与G、H相连,但这两个顶点目前都没有被深度优先遍历访问到,此时的情况、立刻说明从邻接矩阵中无法得到Low,同表28的顶点M情况一致,就是说从H顶点来,而H顶点又来自B,所以K的Low也是5。

这现实意义也很明确:如果把B炸毁了、K就是受害者,当然H也是。
(8) 顶点G,步骤8
还是看G的邻接矩阵:

在这个表中可知:G连接有B、H、I、K,其中B、H、K是深度优先遍历都访问过的,这3个顶点里,以访问B的步骤最小,就是5,于是:

对这个结果还能说什么?意味着B炸掉后又多了个受害者。
(9) 顶点I,步骤9
同样要看邻接矩阵,对于I就是:

这个顶点更不幸,它仅仅与G相连,对于这样的顶点,我们知道访问到G的步骤:8,就是这个顶点的Low,就是:

回忆我们对B-H路径的分析,我们知道此时的G同样是I的关节点,I回到A,必须经过G。如果炸掉G、B这样的顶点,I城市就算没救了。
(10) 顶点D,步骤10
还是先看邻接矩阵,对于D,就是:

可知顶点D与B、E相连,对于D,此时最先抵达的顶点是B,在步骤5,所以有:

这个结果说明B依然是控制着D的生命线。
(11) 顶点E,步骤11
还是看E的邻接矩阵,就是:

可以知道E与D直接相连,于是回边上另一个顶点D、也就是在步骤D,于是:

总结下:设当前顶点为v,下一个顶点是w,其步骤都在Visited[ ]中保存,则:
Low[w]>= Visited[v]
则v必然是关节点,比如此时v是顶点D,而w代表E;或者v是顶点B,而w代表H、K等顶点。
从图5中我们不难发现炸掉D确实能孤立E。
(12) 顶点C,步骤12
还是看邻接矩阵,在顶点C有:

从这个地方可知C与A、B相连,这两个顶点都在第1、5步骤访问过,显然回到A最直接,于是此时Low为1。

由于有这个回边线路,所以看图5我们就知道:炸掉B对这个结点不起任何作用。
最后一个顶点F,看邻接矩阵表可知与A相连,所以表46中自行写入1即可,不再重复计算。
到此,G5图中各个顶点回到A顶点路径上、各个回边和关节点计算完毕,我们回顾这个过程不难发现:A、B、G、D是这个图的关节点。
在关节点上分割图,立刻可以将一个图分割成若干个不相连的子图,这就是图论中对关节点的要求。
2 关节点计算的编程实现
根据上面计算的过程,我们可以总结如下:
关节点的计算首先要获得Low[ ],如设图为G,则计算过程分两种情况:
(1) 深度遍历过程中,如到当前顶点v,如该顶点邻接顶点没有被深度优先遍历访问过,如前面的M、K这两个顶点,则此时该顶点最早回边顶点值(Low)等同前一节点值,也就是:G->Low[v]=G->Low[w];
(2) 在遍历过程中,如到当前顶点v,该结点邻接矩阵中可以找到已经遍历过的邻接顶点,则G->Low[v]= min(G->Visited[w]);,如B、J等。
而关节点的判断条件则是:
遍历过程中,如当前顶点为v,邻接顶点为w,如满足:
G->Low[w]>=G->Visited[v]
如v是顶点B、w是顶点H,则v是关节点。
为了满足上述计算要求,我们首先修改Graph的定义,补充内容如下:
struct Graph
int **pA;
char **pV;
int num;
int *Visited;
int Count;
int *Low;
;
新补充的变量Count是一个计数器,用来计算深度优先遍历的步骤,有这个步骤,我们才能在图5上标注每个结点在深度优先遍历中是在哪一步到达的。而对于Low[ ],我们知道这里是最小回边的次序号,定义为指针是准备按顶点个数来动态申请内存,由此,我们图的初始化函数就是表27。
同表19的程序实际没什么差别,仅仅是初始化了Low[ ]这个数组。
深度优先遍历的过程,同前面的过程实际完全一致,但此时Visited[ ]中将不是简单的把已经访问过得顶点如v设置成1,而是要标记步骤,标记步骤,就是让深度优先遍历的过程中,每次都要进行:
++G->Count;
然后把这个结果赋值给:
G->Visited[v]=Count;
其中v是遍历到当前结点的下标。
所以能标记步骤的深度优先遍历就是表28,运行下这个程序,你会看到遍历结果,逐个将Visited[ ]中的值打印出来,就有了深度优先遍历到每个顶点的步骤。
struct Graph *GraphInit(int n)
int i;
struct Graph *g;
if(n<=0) return NULL;
g=(struct Graph *)malloc(sizeof(struct Graph));
g->num=n;
g->pA=(int **)malloc(sizeof(int )*n);
g->pV=(char **)malloc(sizeof(char)*n);
for(i=0;i<n;i++)
g->pA[i]=(int *)malloc(sizeof(int)*n);
g->pV[i]=(char *)malloc(以上是关于求图的深度优先遍历程序 c语言版的主要内容,如果未能解决你的问题,请参考以下文章