纳什均衡

Posted 2023-04-05 Zeardoe

纳什均衡

一个游戏，\\(A\\) 有 \\(n\\) 种策略，\\(B\\) 有 \\(m\\) 种策略，两方同时出策略，当 \\(A\\) 出了第 \\(i\\) 种，\\(B\\) 出了第 \\(j\\) 种的时候，有一个结果。在这个结果集合里定义有偏序，表示某个结果在 \\(A\\) 看来更优/劣。

双方分别存在一个/一些策略，使得对于 \\(A\\) 和 \\(B\\) 的任何一方，如果其不改变自己的策略，那么另一个人不管如何改变策略，结果对自己不会更优。

\\(A\\) 的策略形如：\\(\\(p_1, p_2, ..., p_n)\\, \\sum p_i = 1, \\forall i, p_i \\in [0, 1]\\)，表示出 \\(1,2,...,n\\) 的概率分别是 \\(p_1,...,p_n\\)。\\(B\\) 同理有 \\(\\(q_1, q_2, ..., q_n)\\\\)。其中，如果存在 \\(p_i = 1\\)，那么 A 一定选择出 \\(i\\)。

这样的策略对任何一方可能都不能达到理想情况下的最优解，但是对两个利己主义者来说，是最稳定的，是对方不管怎么选择自己都最不吃亏的一种策略。

如果纳什均衡点唯一，那么两方的策略固定，两方的期望得分固定。

例子

囚徒困境

假设有两个小偷 A 和 B 联合犯事、私入民宅被警察抓住。警方将两人分别置于不同的两个房间内进行审讯，对每一个犯罪嫌疑人，警方给出的政策是：如果一个犯罪嫌疑人坦白了罪行，交出了赃物，于是证据确凿，两人都被判有罪。如果另一个犯罪嫌疑人也作了坦白，则两人各被判刑 \\(8\\) 年；如果另一个犯罪嫌疑人没有坦白而是抵赖，则以妨碍公务罪（因已有证据表明其有罪）再加刑 \\(2\\) 年，而坦白者有功被减刑 \\(8\\) 年，立即释放。如果两人都抵赖，则警方因证据不足不能判两人的偷窃罪，但可以私入民宅的罪名将两人各判入狱 \\(1\\) 年。

关于案例，显然最好的策略是双方都抵赖，结果是大家都只被判 \\(1\\) 年。但是由于两人处于隔离的情况，首先应该是从心理学的角度来看，当事双方都会怀疑对方会出卖自己以求自保、其次才是亚当·斯密的理论，假设每个人都是“理性的经济人”，都会从利己的目的出发进行选择。这两个人都会有这样一个盘算过程：假如他坦白，如果我抵赖，得坐 \\(10\\) 年监狱，如果我坦白最多才 \\(8\\) 年；假如他要是抵赖，如果我也抵赖，我就会被判一年，如果我坦白就可以被释放，而他会坐 \\(10\\) 年牢。综合以上几种情况考虑，不管他坦白与否，对我而言都是坦白了划算。两个人都会动这样的脑筋，最终，两个人都选择了坦白，结果都被判 \\(8\\) 年刑期。
基于经济学中“理性的经济人”的前提假设，两个囚犯符合自己利益的选择是坦白招供，原本对双方都有利的策略不招供从而均被判处一年就不会出现。这样两人都选择坦白的策略以及因此被判 \\(8\\) 年的结局，纳什均衡”首先对亚当·斯密的“看不见的手”的原理提出挑战：按照斯密的理论，在市场经济中，每一个人都从利己的目的出发，而最终全社会达到利他的效果。但是我们可以从“纳什均衡”中引出“看不见的手”原理的一个悖论：从利己目的出发，结果损人不利己，既不利己也不利他。

零和博弈

定义得分：当 \\(A\\) 出了第 \\(i\\) 种，\\(B\\) 出了第 \\(j\\) 种的时候，得分为 \\(M_i,j\\)，\\(A\\) 的目标是最大化得分，\\(B\\) 的目标是最小化得分，那么这是一个零和博弈。（因为 \\(A\\) 的得分就是 \\(B\\) 的得分的相反数，所以是零和的，这样可以写在一个矩阵内。如果 \\(A\\)，\\(B\\) 都有得分，但是 \\(A\\) 目标是最大化 \\(A-B\\) 的得分，那么也是零和博弈）

在零和博弈中，一定存在纳什均衡，而且可以在矩阵上求出来。

定理：对矩阵 \\(M_i, j\\)，每一行表示 \\(A\\) 选择某一个策略的所有结果；每一列是 \\(B\\) 选择某一个策略的所有结果。考虑 \\(A\\) 的均衡策略：删掉 \\(B\\) 不会选择的所有策略之后，对于 \\(B\\) 选择的每一个策略，期望得分一致的策略也就是 \\(A\\) 的均衡策略。

其中，不会选择的策略指：考虑每列是一个向量 \\((q_1, ..., q_m)\\)，在 \\(m\\) 维空间中的凸包里（不在凸包上）的策略。

也就是一些列消掉之后，形成一个 \\(n \\times m\'\\) 的矩阵，然后对 \\((p_1, ..., p_n)\\) 若满足 \\(C_1 = C_2 = ... = C_m\'\\)，其中 \\(C_i = \\sum_j p_j M_j, i\\)，那么 \\(\\p_n\\\\) 是一个纳什均衡点。

这一等式显然是 \\(m\' - 1\\) 个方程；再加上一个方程 \\(p_1 + p_2 + ... + p_n = 1\\)，总共 \\(m\'\\) 个方程，一定有解（证明比较复杂，运用到 Kakutani 不定点定理，略去），取其中的所有非负整数解即是所有纳什均衡点。（如果有很多解，可能要上线性规划）

做 \\(m\\) 维凸包是困难的。但是有的题目并没有哪个 \\(B\\) 的策略没用，可以这样判断：

直接对矩阵做高斯消元，得出来如果是唯一解，或者是解的每一维都是非负数，那么是纳什均衡。不然的话有凸包内的点要去掉。

P9142 [THUPC 2023 初赛] 欺诈游戏

【题意】

\\[M_x, y = \\begincases 0 & x=y \\\\ x & x>y \\\\ \\cfracy2 & x<y \\endcases \\]

求两方的均衡策略。
\\(n \\le 4 \\times 10^5\\)。
【分析】

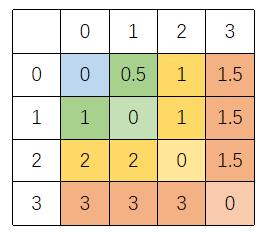
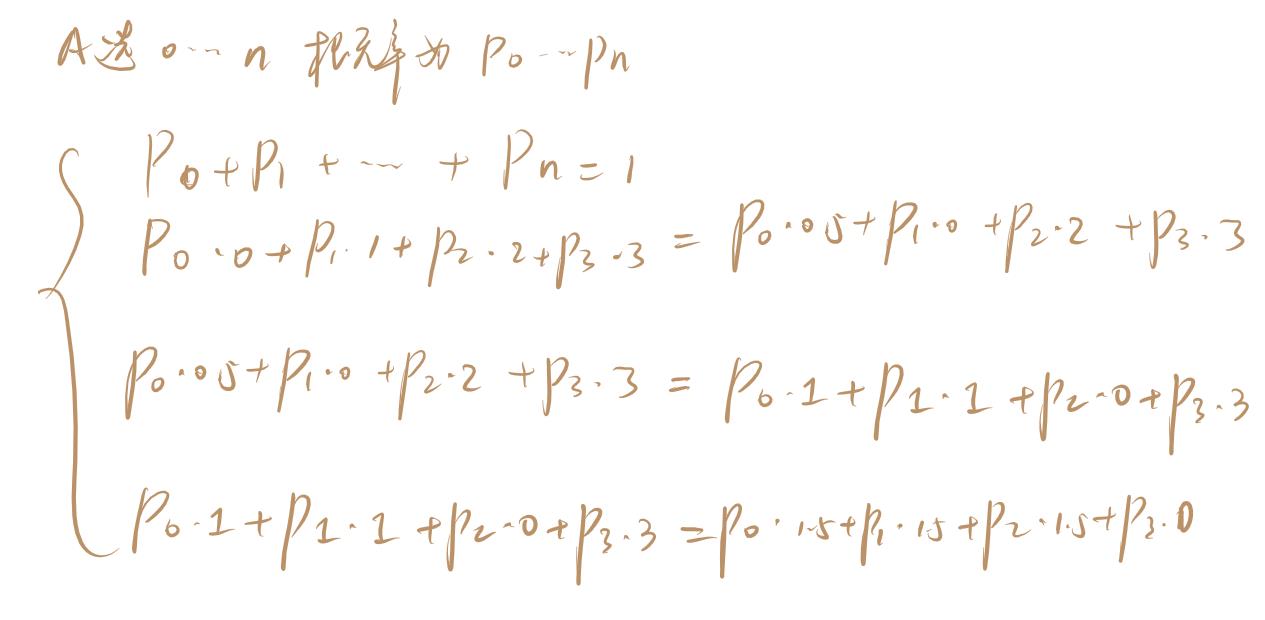
列出行列式：

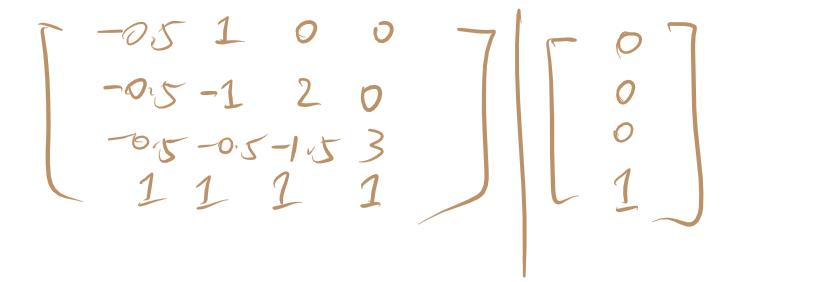
它是一个 \\(d = 2\\) 的带状矩阵，可以 \\(O(n d^2)\\) 的时间求出。

它确实解出来是唯一解，那么就是纳什均衡点。

《纳什均衡与博弈论》纳什博弈论及对自然法则的研究

《纳什均衡与博弈论》纳什博弈论及对自然法则的研究

纳什，《美丽心灵》男主

文章目录

• • 《纳什均衡与博弈论》纳什博弈论及对自然法则的研究
  • @[toc]
  • • 摘录
    • 第八章 培根的链接——网络、社会与博弈
    • 纳什均衡计算

摘录

• 如果说在17世纪，自然哲学家们借助人类世界的法则来研究自然界，那么到了18世纪，就是自然界的定律帮祝我们更好地了解人类生活的时候。 ——罗杰·史密斯《诺顿人类科学史》

• 冯·诺依曼和摩根斯特恩指出：“大数目通常要比小规模的数目更容易处理。”

• 通常，要想让博弈论发挥作用，混合策略是不可或缺的。

• 打扑克牌时，虚张声势不可不免。

• 在二人零和博弈中使用最小最大化原理的奥秘在于，你要铭记，一方赢得什么，另一方就要失去什么（这就是零和博弈的定义）。（在零和博弈中数字代表矩阵左方的局中人的收益）

• 纳什的非合作博弈理论被公认为20世纪人类最杰出的智力成果之一，其意义可与生物界的DNA双螺旋结构的发现向媲美。 ——经济学家罗杰·迈尔森

• 纳什均衡理论：在其他玩家的策略不变时，每个玩家采取的混合策略都最大化其自身收益。

  （百度百科：纳什均衡是指博弈中这样的局面，对于每个参与者来说，只要其他人不改变策略，他就无法改善自己的状况。纳什证明了在每个参与者都只有有限种策略选择并允许混合策略的前提下，纳什均衡定存在。）

• 博弈论中的经典问题：囚徒困境，爱丽丝和鲍勃相关，梅耶的硬币（量子与博弈论）

• 以牙还牙策略

• 瑞德·蒙特格的“人类神经影像实验室”，“将精神和人类经验量化，将感觉转换为数字。”

• “信任，是经济学家已经找到的和经济增长最为相关的因素之一” ——扎克

• 利己主义者敢说各种各样的话和扮演各种各样的角色。 ——拉罗什富科

• 乌合之众人多而智寡。 ——英国谚语

• 不管现实中的人多么变幻莫测，他的行为总是浩瀚宇宙有序体系的一部分。 ——亨利·汤马斯·巴克尔

• 凯特勒（1796生于根特），发明了衡量肥胖的凯特勒指标，即体重指数，简称BIM。

• 历史学家亨利·汤马斯·巴克尔（1821生于伦敦），是一流的国际象棋棋手，能够熟练使用七种语言，并熟知十几门语言，也是收藏丰富的藏书家，藏书超过20000本。

  巴克尔认为：偶尔有人的决策看起来是自由的，甚至是令人惊讶的，那是因为你不了解他的处境。“如果我能够正确推理，同时对他的处境了如指掌，我就能预测由这些处境引发的一系列行为。“

• 博弈论的成功之处在于证明了纯策略的概率分布（混合策略）能够使效应最大化（或损失最小化），特别当你的对手是理性的时候（意味着他们也采取混合策略）。

• 科林·卡莫热指出：“博弈论是描述社会相互作用的数学语言，它为此而生。”

• 是博弈论深及物理学，还是物理学深及博弈论？皆有可能。但令人惊奇的却是，量子物理可能在最基本的层次上成为两者的纽带。 ——李周凡，尼尔·F·约翰逊，《物理世界》

• 所有精确的科学都依赖于并不太精确的近似理念，这看似矛盾，却是事实所在。 ——伯特兰·罗素

---

第八章 培根的链接——网络、社会与博弈

与亚原子的粒子物理学或是宇宙的大尺度结构物理学不同，网络科学是现实世界的科学——一个关于人类、友谊、谣言、疾病、时尚、各类公司和金融危机的世界。 ——邓肯·瓦茨，《六度空间》

六度空间：任何连个陌生人都可以在“六度分离”之内被联系起来，五次周转。 （培根网络，培根是作为“枢纽”来联系其他人的）

不同网络的一种基本共同特征是它们中的很多都呈现出了小世界性质。

瓦茨和斯托加茨推断，“小世界现象不只是社会网络的特例或是人造的理想模型——它可能普遍存在于自然界中的各种大型、稀疏网络中。”

✨

某个网络特征可以用类似气体的温度和压强那样的参数来量化，科学家称其为描述性系统变量。任意两个节点之间的平均步数——路径长度——就是这样一个参数。另一个是“聚合系数”——指的是如果两个点都和第三个相连接时，这两点直接相连的可能性。相对较高的聚合比例是小世界网络违反直觉的特征之一。小世界网络的路径长度和随机网络比较相似。另一方面，小世界网络的高聚合系数则和随机网路完全不同，反而更接近规则网络。

除了聚合系数和路径长度之外，另一个关键的数字是将一个节点和其他节点连接起来的平均连线数量，称为“级度系数”（节点的“级度”是该节点连接的其他节点数量）

✨

个体的最优并能带来群体的最优。

“这个矛盾意味着用户最大化其适宜性的倾向实际上导致了适宜性的下降······”

---

纳什均衡计算

假设鲍勃欠爱丽丝10美元，在爱丽丝的游戏里，他们连续在一个月里面每个工作日都去图书馆一次。如果两个人都是乘车去的，那么鲍勃付给爱丽丝3美元；两人都走路去，则付4美元。鲍勃乘车而爱丽丝走路去，因而爱丽丝后到，鲍勃付5美元；鲍勃走路而爱丽丝鲍勃走路而爱丽丝乘车，因而爱丽丝先到，鲍勃付6美元。

在零和博弈中，收益矩阵中的数字代表矩阵左方的局中人的收益。爱丽丝的收益如下表

	（鲍勃）乘车	（鲍勃）步行
（爱丽丝）乘车	3	6
（爱丽丝）步行	5	4

1️⃣

现在假设爱丽丝选择乘车的概率为p，则步行的概率为1-p。

鲍勃选择乘车的概率为q。则他步行的概率为1-q。

因此

爱丽丝选择乘车的期望收益为$3q+6(1-q)$，选择步行的期望收益为$5q+6(1-q)$。

用相似的推理来计算鲍勃的期望收益可以得到：

鲍勃选择乘车的期望收益为$-3p+[-5(1-p)]$，选择步行的期望收益为$-6p+[-4(1-p)]$。

要达到纳什均衡，他们做两种选择的概率必须使得对这两个概率的任何改变都无法带来更多收益。

对爱丽丝来说，若鲍勃不改变策略，则
$$-3p+[-5(1-p)]=-6p+[-4(1-p)]$$
解得p=1/4。所以对于爱丽丝来说，她选择乘车的最优概率为1/4，对应步行的最优概率为3/4。

若爱丽丝不改变策略，对鲍勃来说，同理可解得q=1/2。所以鲍勃应该在一半时间乘车，一半时间步行。

2️⃣

	（鲍勃）乘车	（鲍勃）步行
（爱丽丝）乘车	3	6
（爱丽丝）步行	5	4

对鲍勃来说，他在选择特定策略的时候爱丽丝选择的策略收益差为-2和2（行数据相减），比例为1:1，可得鲍勃最佳策略为一半乘车，一半步行。

对爱丽丝来说，她在选取特定策略的时候鲍勃采用策略的收益差为-3和1（列数据相减），比例为3:1，可得爱丽丝的最佳策略为1/4时间乘车，3/4时间步行。

.

可以看出，在二人零和博弈中，在很多情况下，最佳策略即混合策略。