Graph Neural Networks for Link Prediction with Subgraph Sketching

Posted 2023-04-05 馒头and花卷

目录

• 概
• 符号说明
  • 必要的定义
• Motivation
• ELPH
• 代码

Chamberlain B. P., Shirobokov S., Rossi E., Frasca F., Markovich T., Hammerla N., Bronstein M. M. Hansmire M. Graph neural networks for link prediction with subgraph sketching. In International Conference on Learning Representations (ICLR), 2023.

概

本文分析了原先的 MPNN 架构以及 subgraph GNN 在 link prediction 任务上的局限性, 以此提出了 ELPH (Efficient Link Prediction with Hashing) 用以结合二者.

符号说明

• \\(\\mathcalV\\), nodes;

• \\(\\mathcalE\\), edges;

• \\(G = (\\mathcalV, E)\\), undirected graph;

• \\(d(u, v)\\), shortest walk length;

• \\(S = (\\mathcalV_S, \\mathcalE_S)\\), subgraph, 满足

  \\[\\mathcalE_S = \\(u, v) \\in \\mathcalE| u, v \\in \\mathcalV_S\\. \\]

• \\(S_uv^k = (\\mathcalV_uv, \\mathcalE_uv)\\), 由边 \\((u, v)\\) 引出的 \\(k\\)-hop subgraph, 其中 \\(\\mathcalV_uv\\) 是 \\(u, v\\) 的 \\(k\\)-hop neighbors.

必要的定义

同构与自同构-graph-level (\\(G_1 \\cong G_2\\)): 假设 \\(G_1 = (V_1, E_1), G_2 = (V_2, E_2)\\) 为两个简单图, 称它们是同构的若存在一双射 \\(\\varphi: V_1 \\rightarrow V_2\\) 满足:

\\[(u, v) \\in E_1 \\Leftrightarrow (\\varphi(u), \\varphi(v)) \\in E_2, \\quad \\forall u, v \\in V_1. \\]

进一步, 若 \\(G_1 = G_2\\), 则称它们为自同构的.

直观上来讲, 两个图同构, 就是存在一一对应的点具有相同的结构.

G-自同构-node-level (\\(u \\sim_G v\\)): 假设 \\(G = (V, E)\\) 为一简单图, \\(u, v\\) 为其中的两个点, 称它们是等价的若存在一双射 \\(\\varphi: V \\rightarrow V\\) 满足:

\\[(a, b) \\in E \\Leftrightarrow (\\varphi(a), \\varphi(b)) \\in E, \\quad \\forall a, b \\in V. \\]

且

\\[u = \\varphi(v). \\]

G-自同构-edge-level (\\((u_1, v_1) \\sim_G (u_2, v_2)\\)): 假设 \\(G = (V, E)\\) 为一简单图, \\((u_1, v_1), (u_2, v_2)\\) 为其中的两条边, 称它们是等价的若存在一双射 \\(\\varphi: V \\rightarrow V\\) 满足:

\\[(a, b) \\in E \\Leftrightarrow (\\varphi(a), \\varphi(b)) \\in E, \\quad \\forall a, b \\in V. \\]

且

\\[u_2 = \\varphi(u_1), v_2 = \\varphi(v_1). \\]

Motivation

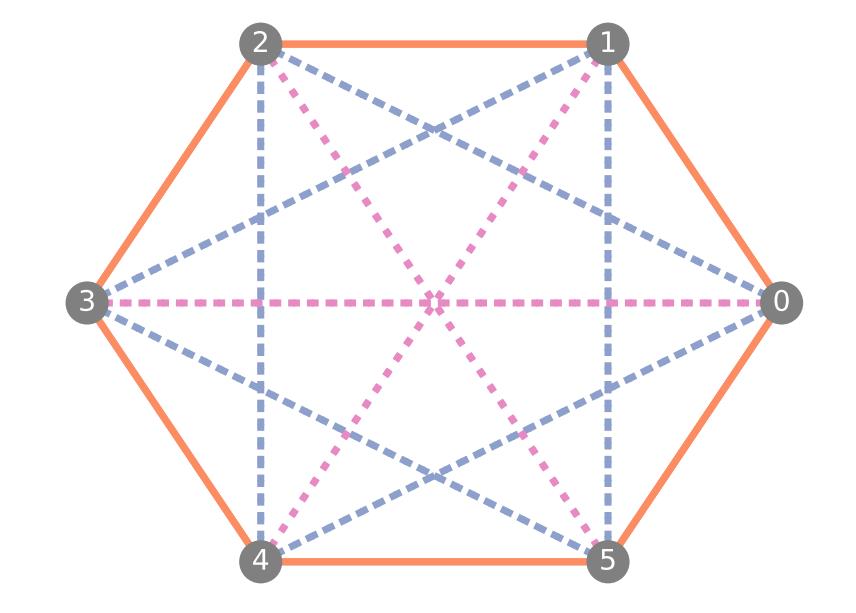
• 首先给出一个事实, 即 \\(u_1 \\sim_G u_2 \\wedge v_1 \\sim v_2 \\not \\Rightarrow (u_1, v_1) \\sim_G (u_2, v_2)\\), 如上图所示:

  1. 所有的点都是自同构的;
  2. 比如取 \\(u_1 = u_2 = n_0, v_1 = n_1, v_2 = n_2\\), 若 \\((u_1, v_1) \\sim_G (u_2, v_2)\\), 则有 \\((n_0, n_2) \\in E\\), 这是错的.

• 但是现在的 MPNN, 强调自己具有和 WL-Test 相当的表达能力, 恰恰意味着不能够很好地解决这个问题 (对于 link prediction 而言).

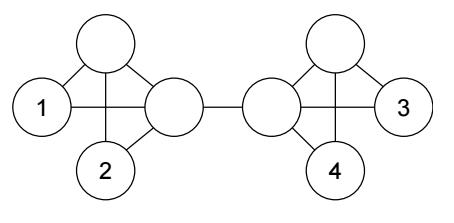
• 如上图所示, 依赖 WL 算法, 倘若我们连接 (1, 2), 那么必定也要连接 (1, 4):

  1. 因为倘若两个结点 \\(v_2 \\sim_G v_4\\) 那么 WL 算法会为两个上同样的色, 可以看成是赋予相同的特征, 不妨设为 \\(\\bmz_2 = \\bmz_4 = \\bmz\\);

  2. 此时, 一般的 link prediction 会通过:

     \\[s_uv = \\phi(\\bmz_u, \\bmz_v) \\]

     计算 score, 就会有

     \\[s_12 = s_14 = \\phi(\\bmz_1, \\bmz). \\]

  3. 此时, 若 (1, 2) 被连接, 那么 (1, 4) 也应当被连接, 但是这和直观上的理解是不符的.

• 当然了, 需要说明的是, 上面的例子有其特殊性, 在实际中, 每个结点都有它的结点 (或者赋予 embedding), 这就导致实际上很难出现 \\(\\bmz_u = \\bmz_v\\) 的情况 (不考虑 over-smoothing).

• 现有的一些基于 subgraph 的方法通过为结点排序来解决这一问题 (见 Palette-WL, SEAL), 但是 subgraph 的提取是复杂的, 且不易并行计算.

ELPH

• 定义

  \\[\\mathcalA_uv[d_u, d_v] := |\\n \\in \\mathcalV: d(n, u) = d_u, d(n, v) = d_v\\|, \\\\ \\mathcalB_uv^k[d] := \\sum_d_v = k+1^\\infty \\mathcalA_uv[d, d_v]. \\]

• ELPH 的每一层为 (共 \\(k\\) 层):

  \\[\\mathbfe_u, v^(l) = \\\\mathcalB_uv[l], \\mathcalA_uv[d_u, l], \\mathcalA_uv[l, d_v] : \\forall d_u, d_v < l\\, \\\\ \\mathbfx_u^(l) = \\gamma^(l) (\\mathbfx_u^(l-1), \\Box_v \\in \\mathcalN(u)\\Big\\ \\phi^(l)(\\mathbfx_u^(l-1), \\mathbfx_v^(l-1), \\mathbfe_u, v^(l)) \\Big\\ ), \\]

  其中 \\(\\Box\\) 是某种 permutation-invaiant aggregation function, 比如 (sum, mean, max). \\(\\mathbfx\\) 是结点特征.

• 最后通过如下方式进行 link prediction:

  \\[p(u, v) = \\psi(\\mathbfx_u^(k) \\odot \\mathbfx_v^(k), \\\\mathcalB_uv[d]\\) \\]

• 总的来说, ELPH 既有 node features, 也有 \'edge\' features.

• 需要注意的是, 在实际中, \\(\\mathcalA, B\\) 的计算是比较复杂的, 所以作者采用的是一种近似方法, 首先注意到:

  \\[\\mathcalA_u,v[d_u, d_v] = |\\mathcalN^d_u(u) \\cap \\mathcalN^d_v(v)| - \\sum_x \\le d_u \\sum_x \\not= y \\le d_v |\\mathcalN^x(u) \\cap \\mathcalN^y(v)|, \\\\ \\mathcalB_uv^k[d] = |\\mathcalN^d(u)| - \\mathcalB^k_uv[d-1] - \\sum_i=1^d \\sum_j=1^d \\mathcalA_uv[i, j], \\]

  其中 \\(\\mathcalN^d(u) := \\v \\in \\mathcalV: d(v, u) \\le d\\\\). 注: 说实话, 我不是很能理解为什么 \\(\\mathcalB\\) 有这样的迭代公式, 我自己推导出来的结果是:

  \\[\\mathcalB_uv^k = |\\mathcalN^d(u)| - |\\mathcalN^d-1(u)| - \\sum_j=1^k \\mathcalA_uv[d, j]. \\]

• 注意, 即使如此, \\(|\\mathcalN^d(u)|\\) 和 \\(|\\mathcalN^d_u(u) \\cap \\mathcalN^d_v(v)|\\) 的计算依然是复杂的, 作者通过 MinHash 和 HyperLogLog 来近似它们.

• 通过 HyperLogLog 近似任意集合的大小 \\(|S|\\):

• 通过 MinHash 近似 Jaccard similarity.

代码

datasketch: hyperloglog; hyperloglog++; minhash

每日一读Pro-GNN：Graph Structure Learning for Robust Graph Neural Networks

目录

• 简介
• 论文简介
• ABSTRACT
• 1 INTRODUCTION
• 2 RELATED WORK
• • 2.1 Graph Neural Networks
  • 2.2 Adversarial Attacks and Defense for GNNs
• 6 CONCLUSION
• 读后总结
• 结语

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3394486.3403049

会议：KDD '20: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining （CCF A类）

代码：https://github.com/ChandlerBang/Pro-GNN

年度：2020年8月20日

ABSTRACT

图神经网络 (GNN) 是图表示学习的强大工具

然而，最近的研究表明

1. GNN 容易受到精心设计的扰动，称为对抗性攻击
2. 对抗性攻击很容易欺骗 GNN 对下游任务进行预测
3. 对抗性攻击的脆弱性引起了人们对在安全关键型应用中应用 GNN 的担忧

因此，开发鲁棒的算法来防御对抗性攻击具有重要意义

---

防御对抗性攻击的一个自然想法是清理扰动图

很明显，现实世界的图共享一些内在属性，例如，许多现实世界的图是低秩和稀疏的，两个相邻节点的特征往往相似

事实上，我们发现对抗性攻击可能会违反这些图属性

因此，在本文中，我们探索这些属性来防御对图的对抗性攻击

特别是，我们提出了一个通用框架 Pro-GNN，它可以从这些属性引导的扰动图中联合学习结构图和鲁棒图神经网络模型

对真实世界图的大量实验表明，与最先进的防御方法相比，即使在图受到严重扰动时，所提出的框架也能实现显着更好的性能

1 INTRODUCTION

图是众多领域中普遍存在的数据结构，例如化学（分子）、金融（交易网络）和社交媒体（Facebook 朋友网络）

随着它们的流行，学习图的有效表示然后将它们应用于解决下游任务尤为重要

近年来，图神经网络 (GNN) [15、18、22、30] 在图的表示学习方面取得了巨大成功

• GNN 遵循消息传递方案 [14]，其中节点嵌入是通过聚合和转换其邻居的嵌入来获得的
• 由于良好的性能，GNN 已被应用于各种分析任务，包括节点分类 [18]、链接预测 [19] 和推荐系统 [35]

---

尽管已经取得了可喜的成果，但最近的研究表明，GNN 容易受到对抗性攻击 [10、17、32、39、40]

换句话说，GNN 的性能会在图中不明显的扰动下大大降低

这些模型缺乏稳健性可能会对与安全和隐私相关的关键应用程序造成严重后果

例如，在信用卡欺诈检测中，欺诈者可以只与少数高信用用户创建多笔交易来伪装自己，从而逃避基于 GNN 的检测

因此，开发强大的 GNN 模型来抵抗对抗性攻击非常重要

修改图形数据可能会扰乱节点特征或图形结构

然而，鉴于结构信息的复杂性，大多数现有的对图数据的对抗性攻击都集中在修改图结构，尤其是添加/删除/重新连接边 [34]

因此，在这项工作中，我们的目标是防御最常见的对图数据的对抗性攻击设置，即对图结构的毒化对抗性攻击

在这种设置下，在训练 GNN 之前修改边已经扰乱了图结构，而节点特征没有改变

---

设计一种有效的防御算法的一个观点是清理扰动图，例如删除对抗性边并恢复删除的边 [28, 38]

从这个角度来看，关键的挑战是我们应该遵循什么标准来清理扰动图

众所周知，现实世界的图通常共享某些属性

• 首先，许多现实世界的干净图是低秩和稀疏的 [37]
  • 例如，在社交网络中，大多数人只与少数邻居有联系，影响用户之间联系的因素很少[13, 37]
• 其次，干净图中的连接节点可能共享相似的特征或属性（或特征平滑度）[25]
  • 例如，在引文网络中，两个相互关联的出版物通常共享相似的主题 [18]

图 1 展示了干净图和污染图的这些属性

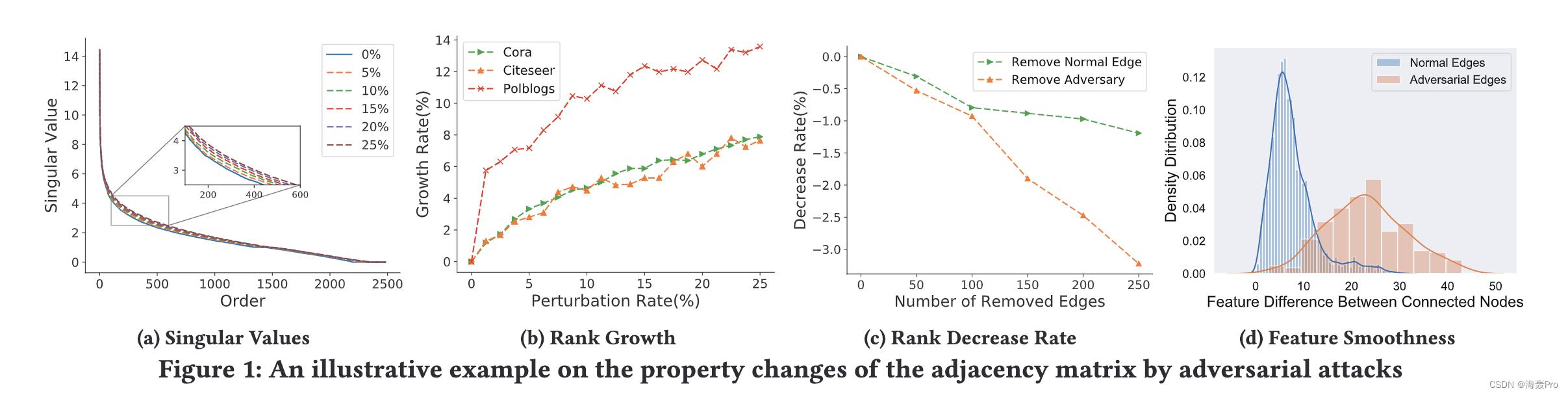
具体来说，我们应用最先进的图中毒攻击metattack [40]来扰乱图数据并可视化mettack前后的图属性

• 如图 1a 所示，metattack 扩大了邻接矩阵的奇异值
• 图 1b 说明了 metaattack 迅速增加了邻接矩阵的秩
• 此外，当我们分别从扰动图中移除对抗边缘和正常边缘时，我们观察到移除对抗边缘比移除正常边缘更快地降低排名，如图 1c 所示
• 此外，我们在图 1d 中描绘了被攻击图的连接节点的特征差异的密度分布。可以观察到，元攻击倾向于连接特征差异较大的节点

图 1 中的观察结果表明，对抗性攻击可能会违反这些属性

因此，这些属性有可能作为清理扰动图的指导

然而，探索这些属性以构建强大的图神经网络的工作相当有限

---

在本文中，我们的目标是探索图的稀疏性、低秩和特征平滑度的特性，以设计鲁棒的图神经网络

请注意，可能还有更多属性需要探索，我们希望将其留作未来的工作

从本质上讲，我们面临着两个挑战：

• （i）如何从这些属性引导的中毒图数据中学习干净的图结构
• （ii） 如何联合学习鲁棒图神经网络和干净结构的参数

为了解决这两个挑战，我们提出了一个通用框架Property GNN（Pro-GNN），以同时从扰动图和GNN参数中学习干净的图结构，以防御对抗性攻击

对各种真实世界图的广泛实验表明，我们提出的模型可以有效地防御不同类型的对抗性攻击，并且优于最先进的防御方法

2 RELATED WORK

根据我们工作的重点，我们简要描述了 GNN 的相关工作，以及图数据的对抗性攻击和防御。

2.1 Graph Neural Networks

在过去的几年里，图神经网络在解决图数据上的机器学习问题方面取得了巨大成功

为了学习图数据的有效表示，已经提出了两个主要的 GNN 家族，即光谱方法和空间方法

第一个家族基于图谱理论[6,11,18]学习节点表示。布鲁纳等人

• [6] 通过使用给定图的傅里叶基，将卷积运算从欧几里得数据推广到非欧几里得数据
• 为了简化光谱 GNN，Defferrard 等人。 [11] 提出 ChebNet 并利用 Chebyshev 多项式作为卷积滤波器。基普夫等人
• [18] 提出 GCN 并通过使用其一阶近似来简化 ChebNet
• 此外，简单图卷积 (SGC) [31] 将图卷积减少为线性模型，但仍能获得具有竞争力的性能

第二类模型将空间域中的图卷积定义为聚合和转换局部信息 [14、15、30]

• DCNN [2] 将图卷积视为扩散过程，并为从一个节点传输到相邻节点的信息分配一定的转移概率。汉密尔顿等人
• [15]建议通过采样和聚合邻居信息来学习聚合器
• Veličković 等人 [30] 提出了图注意力网络 (GAT)，以在聚合信息时学习邻居的不同注意力分数
• 为了进一步提高训练效率，FastGCN [8] 将图卷积解释为嵌入函数在概率度量下的积分变换，并执行重要性采样以对每一层的固定数量的节点进行采样

2.2 Adversarial Attacks and Defense for GNNs

广泛的研究表明，深度学习模型容易受到对抗性攻击

换句话说，对输入的轻微或不明显的扰动可以欺骗神经网络输出错误的预测

GNN 也遇到这个问题 [5 , 10 , 17 , 23 , 24 , 32, 39 , 40 ]

与图像数据不同，图结构是离散的，节点相互依赖，因此更具挑战性

• nettack [39] 通过保留度分布和对特征共现施加约束来产生不明显的扰动
• RL-S2V [10] 采用强化学习来生成对抗性攻击

然而，这两种方法都是为针对性攻击而设计的，只能降低 GNN 在目标节点上的性能

为了在全局范围内扰动图，提出了元攻击 [40] 来生成基于元学习的中毒攻击。尽管已经越来越多地致力于开发对图数据的对抗性攻击，但关于提高 GNN 鲁棒性的研究才刚刚开始 [28 , 32 , 38 , 41 ]

解决这个问题的一种方法是通过惩罚对抗性边缘的注意力分数来学习一个健壮的网络

• RGCN [38] 将高斯分布建模为隐藏层，以吸收对抗性攻击对方差的影响

PA-GNN [28] 利用来自干净图的监督知识，并应用元优化方法来学习鲁棒图神经网络的注意力分数

但是，它需要来自相似领域的额外图形数据

另一种方法是对扰动图进行预处理以获得干净的图并在干净的图上训练 GNN。吴等。 al [32] 发现攻击者倾向于连接到具有不同特征的节点，他们建议删除不同节点之间的链接

Entezari 等人 [12] 观察到 nettack 会导致图的高秩谱发生变化，并建议使用其低秩近似对图进行预处理

然而，由于两阶段预处理方法的简单性，它们可能无法抵御复杂的全局攻击。

与上述防御方法不同，我们旨在探索重要的图属性以恢复干净的图，同时学习 GNN 参数，这使得所提出的模型能够从不同攻击下的扰动图中提取内在结构。

6 CONCLUSION

图神经网络很容易被图对抗攻击所欺骗。为了防御不同类型的图对抗攻击，我们引入了一种新颖的防御方法 Pro-GNN，它可以同时学习图结构和 GNN 参数

我们的实验表明，我们的模型始终优于最先进的基线，并提高了在各种对抗性攻击下的整体鲁棒性

未来，我们的目标是探索更多属性，以进一步提高 GNN 的鲁棒性

读后总结

了解到使用GNN面临的数据扰动问题（这个确实可以好好考虑一下）

暂时mark一下！

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正