BFGS算法中的SWM公式应用
Posted 来者可追
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BFGS算法中的SWM公式应用相关的知识,希望对你有一定的参考价值。
BFGS算法矩阵$ B_k $的迭代公式为:
$$B_k+1=B_k+\\fracy_ky_k^Ty_k^T\\delta_k-\\fracB_k\\delta_k\\delta_k^TB_k\\delta_k^TB_k\\delta_k$$
Sherman-Morrison公式为:
假设 A 是 n 阶可逆矩阵, t 为常量,u,v 是 n 维向量,且 $A+uv^T $也是可逆矩阵,则
$$(A+\\fracuv^Tt)^-1=A^-1-\\fracA^-1uv^TA^-1t+v^TA^-1u$$
下面我们需要根据上述两个式子,得到$B_k+1$的逆矩阵$H_k+1$的迭代格式。注意下面推导过程中第二个等号和第三个等号分别利用了一次Sherman-Morrison公式。\\beginalign* & B_k+1^-1 =(B_k+\\fracy_ky_k^Ty_k^Ts_k-\\fracB_ks_ks_k^TB_ks_k^TB_ks_k)^-1\\\\ &=(B_k+\\fracy_ky_k^Ty_k^Ts_k)^-1+(B_k+\\fracy_ky_k^Ty_k^Ts_k)^-1\\fracB_ks_ks_k^TB_ks_k^TB_ks_k-s_k^TB_k(B_k+\\fracy_ky_k^Ty_k^Ts_k)^-1B_ks_k(B_k+\\fracy_ky_k^Ty_k^Ts_k)^-1\\\\ &=(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)+(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^T\\delta_k+y_k^TB_k^-1y_k)\\fracB_ks_ks_k^TB_ks_k^TB_ks_k-s_k^TB_k(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)B_ks_k(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)\\\\ &=(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)+(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)\\fracB_ks_ks_k^TB_k\\fracs_k^Ty_ky_k^Ts_ky_k^Ts_k+y_k^TB_k^-1y_k(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)\\\\ &=(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)+\\fracB_k^-1B_ks_ks_k^TB_kB_k^-1\\fracs_k^Ty_ky_k^Ts_ky_k^Ts_k+y_k^TB_k^-1y_k-\\fracB_k^-1B_ks_ks_k^TB_k\\fracs_k^Ty_ky_k^Ts_ky_k^Ts_k+y_k^TB_k^-1y_k\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k\\fracB_ks_ks_k^TB_k\\fracs_k^Ty_ky_k^Ts_ky_k^Ts_k+y_k^TB_k^-1y_kB_k^-1+\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k\\fracB_ksa_ks_k^TB_k\\fracs_k^Ty_ky_k^Ts_ky_k^Ts_k+y_k^TB_k^-1y_k\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k\\\\ &=(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k)+\\fracs_ks_k^T(y_k^Ts_k+y_k^TB_k^-1y_k)s_k^Ty_ky_k^Ts_k-\\fracs_ks_k^Ty_ky_k^TB_k^-1s_k^Ty_ky_k^Ts_k- \\fracB_k^-1y_ky_k^Ts_ks_k^Ts_k^Ty_ky_k^Ts_k+\\fracB_k^-1y_k(y_k^Ts_ks_k^Ty_k)y_k^TB_k^-1(y_k^Ts_k+y_k^TB_k^-1y_k)(s_k^Ty_ky_k^Ts_k)\\\\ &=(B_k^-1-\\fracB_k^-1y_ky_k^TB_k^-1y_k^Ts_k+y_k^TB_k^-1y_k) +\\fracs_ks_k^T(y_k^Ts_k+y_k^TB_k^-1y_k)(s_k^Ty_k)^2 -\\fracs_k(s_k^Ty_k)y_k^TB_k^-1(s_k^Ty_k)^2 -\\fracB_k^-1y_k(y_k^Ts_k)s_k^T(s_k^Ty_k)^2+\\fracB_k^-1y_ky_k^TB_k^-1(y_k^Ts_k+y_k^TB_k^-1y_k)\\\\ &=B_k^-1 +\\fracs_ks_k^T(y_k^Ts_k)(s_k^Ty_k)^2 +\\fracs_ks_k^T(y_k^TB_k^-1y_k)(s_k^Ty_k)^2 -\\fracs_ky_k^TB_k^-1s_k^Ty_k -\\fracB_k^-1y_ks_k^Ts_k^Ty_k\\\\ &=B_k^-1 -\\fracB_k^-1y_ks_k^Ts_k^Ty_k -\\fracs_ky_k^TB_k^-1s_k^Ty_k +\\fracs_k(y_k^TB_k^-1y_k)s_k^T(s_k^Ty_k)^2 +\\fracs_ks_k^Ts_k^Ty_k\\\\ &=B_k^-1(I-\\fracy_ks_k^Ts_k^Ty_k) -\\fracs_ky_k^TB_k^-1s_k^Ty_k(I-\\fracy_ks_k^Ts_k^Ty_k) +\\fracs_ks_k^Ts_k^Ty_k\\\\ &=(I-\\fracs_ky_k^Ts_k^Ty_k)B_k^-1(I-\\fracy_ks_k^Ts_k^Ty_k)+\\fracs_ks_k^Ts_k^Ty_k\\\\ &=(I-\\fracs_ky_k^Ts_k^Ty_k)B_k^-1(I-\\fracs_ky_k^Ts_k^Ty_k)^T+\\fracs_ks_k^Ts_k^Ty_k \\endalign*
记:$H_k=B_k^-1,H_k+1=H_k+1^-1$,则有
$$H_k+1=(I-\\fracs_ky_k^Ts_k^Ty_k)H_k(I-\\fracs_ky_k^Ts_k^Ty_k)^T+\\fracs_ks_k^Ts_k^Ty_k$$
本文参考这篇知乎文章:
Broyden类算法:BFGS算法的迭代公式推导(应用两次Sherman-Morrison公式) - 知乎 (zhihu.com)
本文来自博客园,作者:来者可追2019,转载请注明原文链接:https://www.cnblogs.com/wjma2719/p/17285935.html
Pytorch优化器全总结牛顿法BFGSL-BFGS 含代码
目录
优化器系列文章列表
Pytorch优化器全总结(一)SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结(二)Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam
Pytorch优化器全总结(三)牛顿法、BFGS、L-BFGS 含代码
写在前面
这篇文章是优化器系列的第三篇,主要介绍牛顿法、BFGS和L-BFGS,其中BFGS是拟牛顿法的一种,而L-BFGS是对BFGS的优化,那么事情还要从牛顿法开始说起。
一、牛顿法
函数最优化算法方法不唯一,其中耳熟能详的包括梯度下降法,梯度下降法是一种基于迭代的一阶优化方法,优点是计算简单;牛顿法也是一种很重要的优化方法,是基于迭代的二阶优化方法,优点是迭代次数少,收敛速度很快。下面我们简要介绍一下牛顿法。
1.看图理解牛顿法
最优化问题就是寻找能使函数最小化的x,所以目标函数应当是一个凸函数(起码是局部凸函数),假如一个函数如下图:

图1
他的一阶导数可能长下面这个样子:
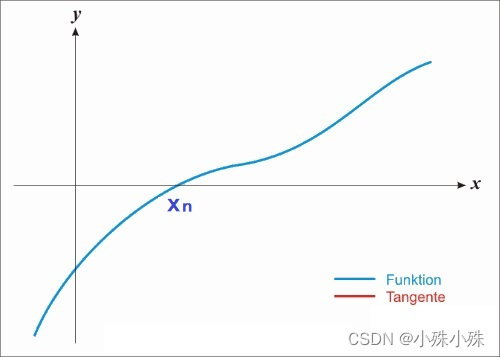
图2
很显然函数在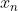 处取得最小值,同时这个点的导数等于0,如果使用梯度下降,经过多次迭代,x的取值会慢慢接近
处取得最小值,同时这个点的导数等于0,如果使用梯度下降,经过多次迭代,x的取值会慢慢接近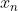 ,我们都能想象这个过程。
,我们都能想象这个过程。
如果使用牛顿法,x也会逼近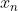 ,不过速度会快很多,示例图如下:
,不过速度会快很多,示例图如下:
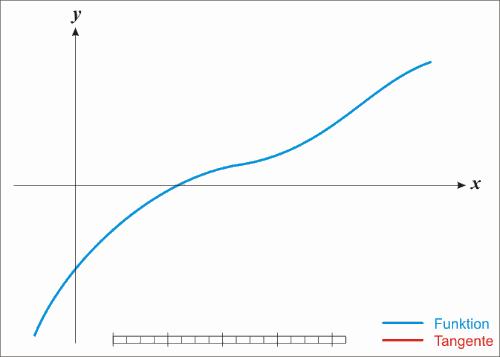
图3
这个过程可以这样描述:
a.在X轴上随机一点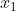 ,经过
,经过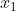 做X轴的垂线,得到垂线与函数图像的交点
做X轴的垂线,得到垂线与函数图像的交点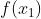 .
.
b.通过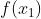 做函数的切线,得到切线与X轴的交点
做函数的切线,得到切线与X轴的交点 .
.
c.迭代a/b两步,当前后两次求的x相同或者两个值的差小于一个阈值的时候,我们就认为找到了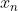 。
。
三个步骤的难点在于b,如何快速的找到切线与X轴的交点,下面有两种计算方式,思想不同但结果是一样的。
2.公式推导-三角函数

图4
如图4,蓝色的线是函数的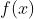 的导数
的导数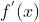 ,则曲线在
,则曲线在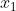 处的导数为
处的导数为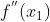 ,我们要求
,我们要求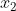 ,根据三角函数有:
,根据三角函数有:
 (1)
(1)
得出:
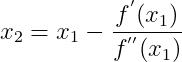 (2)
(2)
利用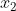 开始进行下一轮的迭代。迭代公式可以简化如下:
开始进行下一轮的迭代。迭代公式可以简化如下:
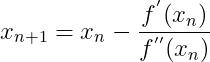 (3)
(3)
3.公式推导-二阶泰勒展开
任意一点在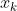 附近的二阶泰勒展开公式为:
附近的二阶泰勒展开公式为:
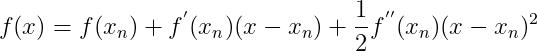 (4)
(4)
对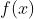 求导:
求导:
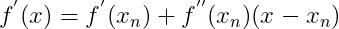 (5)
(5)
令 :
:
 (6)
(6)
写成迭代形式:
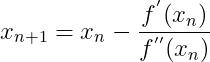 (7)
(7)
可以看到使用三角函数和二阶泰勒展开最终得到的结果是一样的。虽然牛顿法收敛速度很快,但是当x的维度特别多的时候,我们想求得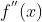 是非常困难的,而牛顿法又是一个迭代算法,所以这个困难我们还要面临无限多次,导致了直接使用牛顿法最为优化算法很难实际落地。为了解决这个问题出现了拟牛顿法,下面介绍一种拟牛顿法BFGS,主要就是想办法一种方法代替二阶导数。
是非常困难的,而牛顿法又是一个迭代算法,所以这个困难我们还要面临无限多次,导致了直接使用牛顿法最为优化算法很难实际落地。为了解决这个问题出现了拟牛顿法,下面介绍一种拟牛顿法BFGS,主要就是想办法一种方法代替二阶导数。
二、BFGS公式推导
函数 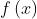 在
在 处的二阶泰勒展开式为:
 (8)
(8)
当x为向量的时候,上式写成:
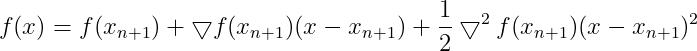
(9)
令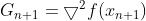 ,同时对
,同时对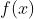 求导:
求导:
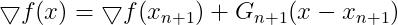 (10)
(10)
接下来我们要想办法去掉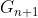 ,我们使用
,我们使用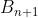 代替
代替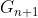 ,
,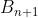 是在迭代中一点点计算出来的而不使用二阶导数。
是在迭代中一点点计算出来的而不使用二阶导数。
上式变为:
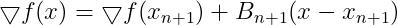 (11)
(11)
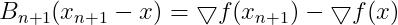 (12)
(12)
我们认为每次迭代 与上次变化
与上次变化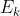 ,形式如下:
,形式如下:
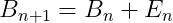 (13)
(13)
令:
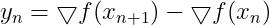 ,
, 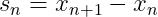 (14)
(14)
将式(13)(14)带入式子(12):
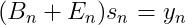 (15)
(15)
令:
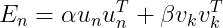 (16)
(16)
其中 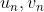 均为
均为 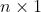 的向量,带入(15)
的向量,带入(15)
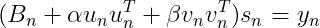 (17)
(17)
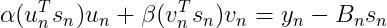 (18)
(18)
已知: 为实数,
为实数,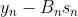 为向量。式(18)中,参数
为向量。式(18)中,参数 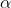 和
和  解的可能性有很多,我们取特殊的情况,假设
解的可能性有很多,我们取特殊的情况,假设  。带入(16)得:
。带入(16)得:
 (19)
(19)
将  带入(18)得:
带入(18)得:
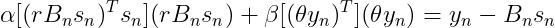 (20)
(20)
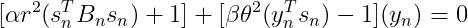 (21)
(21)
令 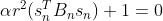 ,则:
,则:
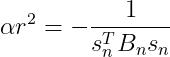 (22)
(22)
令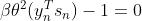 ,则
,则
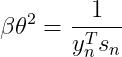 (23)
(23)
将式(22)和(23)带入(19):
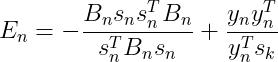 (24)
(24)
将(24)带入(13)得到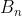 的迭代公式:
的迭代公式:
 (24)
(24)
当x为向量的时候,式(7)写成:
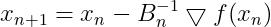 (25)
(25)
加上学习率得到BFGS的迭代公式:
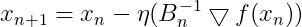 (26)
(26)
我们发现,还需要求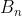 的逆,这里可以引入sherman-morrism公式,求解
的逆,这里可以引入sherman-morrism公式,求解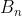 的逆:
的逆:
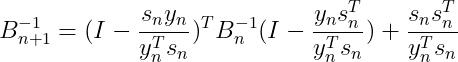 (27)
(27)
我们用 代替
代替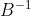 ,得到最终的BFGS迭代公式和
,得到最终的BFGS迭代公式和 的迭代公式:
的迭代公式:
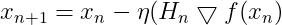 (28)
(28)
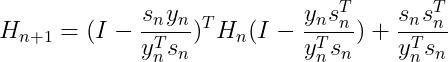 (29)
(29)
其中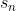 是本轮x与上一轮x的差,
是本轮x与上一轮x的差,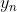 是本轮梯度与上一轮梯度的差。
是本轮梯度与上一轮梯度的差。
三、L-BFGS
在BFGS算法中,仍然有缺陷,每次迭代计算需要前次迭代得到的

令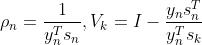 ,则式(29)可以表示为:
,则式(29)可以表示为:
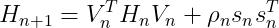 (30)
(30)
若在初始时,假定初始的矩阵
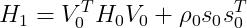 (31)
(31)
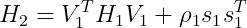

 (32)
(32)
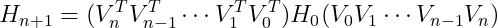
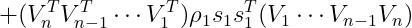

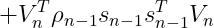
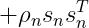
假设当前迭代为n,只保存最近的m次迭代信息,按照上面的方式迭代m次,可以得到如下的公式:
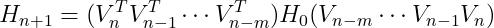
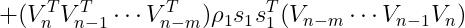

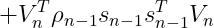
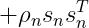
由于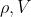 这些变量都最终可以由s、y两个向量计算得到,因此,我们只需存储最后m次的s、y向量即可算出
这些变量都最终可以由s、y两个向量计算得到,因此,我们只需存储最后m次的s、y向量即可算出

四、算法迭代过程
1. 选初始点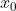 ,最小梯度阈值
,最小梯度阈值 ,存储最近 m 次的选代数据;
,存储最近 m 次的选代数据;
2.初始化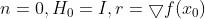 ;
;
3.如果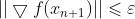 ,则返回最优解 x,否则转入步骤4;
,则返回最优解 x,否则转入步骤4;
4.计算本次选代的可行方向 ;
;
5.计算步长 ,用下面的式子进行线搜索;
,用下面的式子进行线搜索;
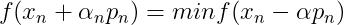
6.用下面的更新公式更新x;
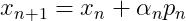
7.如果 n大于 m,保留最近 m 次的向量对,删除 ;
;
8.计算并保存向量对
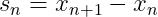
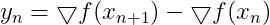
9.用 two-loop recursion算法求:
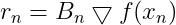
10.设置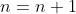 ,转到步骤3
,转到步骤3
五、代码实现
1.torch.optim.LBFGS说明
该类实现 LBFGS优化方法。LBFGS是什么已经不用多说了。
Pytorch说明文档:LBFGS — PyTorch 1.13 documentation
'''
lr (float): 学习率 (default: 1)
max_iter (int): 每个优化步骤的最大迭代次数,就像图3那样迭代 (default: 20)
max_eval (int): 每次优化函数计算的最大数量,使用了线搜索算法时,每次迭代计数器可能增加不止1,最好使用线搜索算法时再设置这个参数。计数器同时受max_iter 和max_eval约束,先到哪个值直接跳出迭代。(default: max_iter * 1.25).
tolerance_grad (float): 一阶最优终止公差,就是指yn (default: 1e-5).
tolerance_change (float): 函数值/参数变化的终止容差,就是指sn (default: 1e-9).
history_size (int): 更新历史记录大小 (default: 100).
line_search_fn (str): 使用线搜索算法,只能是'strong_wolfe' 或者None (default: None).
'''
class torch.optim.LBFGS(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)2.使用LBFGS优化模型
我们用一个简单的全连接网络并使用LBFGS优化,下面是代码和运行结果,可以看到,损失下降的速度还是很快的。
# coding=utf-8
#================================================================
#
# File name : optim_duibi.py
# Author : Faye
# Created date: 2022/8/26 17:30
# Description :
#
#================================================================
import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
# 超参数
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# 生成假数据
# torch.unsqueeze() 的作用是将一维变二维,torch只能处理二维的数据
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1) # x data (tensor), shape(100, 1)
# 0.2 * torch.rand(x.size())增加噪点
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))
# 定义数据库
dataset = Data.TensorDataset(x, y)
# 定义数据加载器
loader = Data.DataLoader(dataset=dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=0)
# 定义pytorch网络
class Net(torch.nn.Module):
def __init__(self, n_features, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_features, n_hidden)
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
y = self.predict(x)
return y
# 定义不同的优化器网络
net_LBFGS = Net(1, 10, 1)
# 选择不同的优化方法
opt_LBFGS = torch.optim.LBFGS(net_LBFGS.parameters(), lr=LR, max_iter=20)
nets = [net_LBFGS]
optimizers = [opt_LBFGS]
# 选择损失函数
loss_func = torch.nn.MSELoss()
# 不同方法的loss
loss_LBFGS = []
# 保存所有loss
losses = [loss_LBFGS]
# 执行训练
for epoch in range(EPOCH):
for step, (batch_x, batch_y) in enumerate(loader):
var_x = Variable(batch_x)
var_y = Variable(batch_y)
for net, optimizer, loss_history in zip(nets, optimizers, losses):
if isinstance(optimizer, torch.optim.LBFGS):
def closure():
y_pred = net(var_x)
loss = loss_func(y_pred, var_y)
optimizer.zero_grad()
loss.backward()
return loss
loss = optimizer.step(closure)
else:
# 对x进行预测
prediction = net(var_x)
# 计算损失
loss = loss_func(prediction, var_y)
# 每次迭代清空上一次的梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新梯度
optimizer.step()
# 保存loss记录
loss_history.append(loss.data)
# 画图
labels = ['LBFGS']
for i, loss_history in enumerate(losses):
plt.plot(loss_history, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()

牛顿法、BFGS和L-BFGS就介绍到这里,后面我将对比所有优化算法的性能,收藏关注不迷路。
优化器系列文章列表
Pytorch优化器全总结(一)SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结(二)Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam
Pytorch优化器全总结(三)牛顿法、BFGS、L-BFGS 含代码
以上是关于BFGS算法中的SWM公式应用的主要内容,如果未能解决你的问题,请参考以下文章
牛顿法|阻尼牛顿法|拟牛顿法|DFP算法|BFGS算法|L-BFGS算法