Online Continual Learning with Maximally Interfered Retrieval---阅读笔记

Posted 2023-04-04 ZLey

Online Continual Learning with Maximally Interfered Retrieval---阅读笔记

摘要：

本文主要提出了一种可控的样本采集策略的重放方法。我们检索受干扰最大的样本，即它们的预测将受到预测参数更新的最大负面影响。

1 Introduction

人工神经网络在完成个体狭窄任务方面的性能已经超过了人类的水平。然而，与能够不断学习和执行无限数量的任务的人类智力相比，这种成功仍然是有限的。人类一生中学习和积累知识的能力对现代机器学习算法，特别是神经网络来说一直是一个挑战。从这个角度来看，持续学习的目标是通过为人工智能代理提供从非固定的、无源不断的数据流中在线学习的能力，从而获得更高水平的机器智能。这是这种永无休止的学习过程的一个关键部分是克服灾难性遗忘。到目前为止开发的解决方案通常将持续学习的问题简化为更容易的任务增量设置，其中数据流可以划分为边界明确的任务，每个任务都是离线学习的。这里的一个任务可以是识别手写的数字，而另一种不同类型的车辆。

根据关于先前任务数据的信息如何被存储和用于减轻遗忘和潜在地支持新任务的学习，现有的方法可以分为三个主要的类型。这些方法包括存储先前样本的基于重放的方法，添加和删除组件的动态架构，以及依赖于正则化的优先聚焦的方法。

在这项工作中，我们考虑一个在线连续设置，其中样本流只看到一次，并且不是iid。这是一个比更温和的增量任务假设更困难和更现实的设置，可以在实践中遇到，例如社交媒体应用程序。我们关注的是基于重放的方法，与其他方法相比，该方法已被证明在在线持续学习设置中被证明是成功的。在这类方法中，以前的知识要么直接存储在重放缓冲区中，要么被压缩在生成模型中。当从新数据中学习时，旧的例子会从回放缓冲区或生成模型中复制。

在这项工作中，假设有一个重放缓冲区或生成模型，我们将注意力转向回答当收到新样本时，应该从以前的历史中重播什么样本的问题。考虑到模型的估计参数更新，我们选择检索遭受损失增加的样本。这种方法也从神经科学中获得了一些动机，其中先前记忆的重放被假设存在于哺乳动物的大脑中，但可能不是随机的。类似的机制可能发生，以适应最近的事件，同时保留旧的记忆。

我们表示了我们的方法，最大限度地干扰检索（MIR），并提出了使用存储的记忆和生成模型的变体。

2 Related work

持续学习的主要挑战是一旦获得新知识，先前知识的灾难性遗忘，这与生物和人工神经网络中存在的稳定性/可塑性困境密切相关。虽然这些问题在早期的研究工作中被研究，但自从神经网络的复兴以来，它们受到越来越多的关注。

已经发展了几种方法来预防或减轻灾难性的遗忘现象。在固定的架构设置下，可以确定两个主要的工作： i)方法依赖于回放样本或虚拟（生成）样本从以前的历史而学习新的和ii)方法编码之前的任务的知识之前用于规范化的训练新任务。虽然先前关注的方法可能在具有少量不相交任务的任务增量设置中很有效，但当任务相似和训练模型面对长序列时，这个家庭往往表现较差。

从以前的历史中重放的样本可以用来约束基于新样本的参数更新，以保持在前一个的可行区域，或者用于排练。在这里，我们考虑一种对以前历史的样本的排练方法，因为它是约束优化方法更便宜和有效的替代方法。排练方法通常使用来自缓冲区的随机样本，或来自根据先前数据训练的生成模型的伪样本。这些工作在离线增量任务设置中显示出了很有希望的结果，最近被扩展到在线设置，其中一系列的任务形成了一个非i.i.d.一次考虑一个或几个样本。然而，在在线设置中，给定有限的计算预算，不能每次重放所有缓冲样本对于选择要重播的最佳候选人变得至关重要。在这里，我们提出了一个比随机抽样更好的策略来改善学习行为和减少干扰。持续学习最近也被研究用于学习生成模型的案例。使用了一个自动编码器来存储压缩表示，而不是原始样本。在这项工作中，我们将利用这一研究方向，并将首次考虑在在线持续学习设置中的生成式建模。

3 Methods

我们的目标是学习一个由\\(θ\\)参数化的分类器\\(f\\)，它使数据流中新样本的预定义损失L最小化，而不干扰或增加之前观察到的样本的损失。鼓励这种情况的一种方法是对存储历史中的旧样本进行更新，或者对基于以前数据训练的生成模型进行更新。我们建议的主要思想是，我们不是使用从以前的历史中随机选择或生成的样本，而是发现受到最大新传入样本(s)的干扰的样本。这是由于观察到，对以前的一些样本的丢失可能不会受到影响，甚至会得到改进，因此对它们进行再训练是一种浪费。

3.1 Maximally Interfered Sampling from a Replay Memory

我们首先在经验重放（ER）的上下文中实例我们的方法，这是一种最近成功的排练方法，它存储了以前样本的一小部分，并使用它们来增加传入的数据。在这种方法中，learner被分配一个有限大小的内存M，当样本流到达时，通过使用水库采样进行更新。通常，样本是从内存中随机抽取的，并与传入的批处理相连接起来。给定一个标准的目标\\(\\min_\\thetaL\\left(f_\\theta\\left(X_t\\right),Y_t\\right)\\) ，当接收到样本\\(X_t\\) 时，我们估计输入批次的参数更新为\\(\\theta^v=\\theta-\\alpha\\nabla L\\left(f_\\theta\\left(X_t\\right),Y_t\\right)\\) 我们现在可以使用该准则\\(s_M I-1(x)=l\\left(f_\\theta^v(x),y\\right)-l\\left(f_\\theta(x),y\\right)\\)搜索前k值\\(x∈M\\) ，其中\\(l\\)是样本损失。我们还可以增加内存，以额外存储迄今为止观察到的最佳\\(l\\left(f_\\theta(x),y\\right)\\) 即为\\(l\\left(f_\\theta^*(x),y\\right)\\) 。因此，我们可以进行评估\\(s_M I-2(x)=l\\left(f_\\theta v(x),y\\right)-\\min\\left(l(f_\\theta(x),y),l(f_\\theta^*(x),y)\\right)\\)

3.2 Maximally Interfered Sampling from a Generative Model

我们现在考虑从生成模型中回放的情况。假设一个由\\(θ\\)参数化的函数\\(f\\)和一个分别由\\(φ\\)和\\(γ\\)参数化的编码器\\(q_φ\\)和解码器\\(g_γ\\)模型。我们可以像前一节一样计算潜在的参数更新\\(θ_v\\)。我们希望在给定的特征空间数据点中找到最大的估计参数更新前后的损失之间的差异：

\\[\\max\\limits_\\mathbfZ\\mathcalL\\big(f_\\theta^v(g_\\gamma(g_\\gamma(\\mathbfZ)),\\mathbfY^*\\big)-\\mathcalL\\bigl(f_\\theta^\'(g_\\gamma(\\mathbfZ)),\\mathbfY^\\ast\\bigr)\\quad\\mathrms.t.\\quad||z_i-z_j||_2^2>\\epsilon\\forall z_i,z_j\\in\\mathbfZ\\mathrmwithz_i\\neq z_j \\tag 1 \\]

这里的\\(\\theta^\'\\)可以对应于当前的模型参数或者历史模型的参数, 此外，\\(y∗\\)表示真实标签，即真实数据分布给生成样本的标签。我们将简短的解释如何近似这个值。我们将约束转换为正则化器，并对方程1进行优化，表示多样性项的强度为\\(λ\\)。从这些点上，我们重建了完整对应的输入样本\\(X^\' = g_\\gamma(Z)\\)，并使用它们来估计新的参数更新\\(\\underset\\theta\\textmin\\mathcalL(f_\\theta(\\boldsymbolX_t\\cup\\boldsymbolX^\'))\\)。

为了评估公式1中的损失，我们还需要对\\(y∗\\)进行评估，一种简单的方法是基于生成回放思想存储先验模型的预测。因此，我们建议使用\\(f_θ^\'\\)给出的预测标签作为伪标签来估计\\(y∗\\)。\\(y_pre = f_\\theta\'(g_\\gamma (z))\\) 和\\(\\haty=f_\\theta^v(g_\\gamma(z))\\) 我们计算KL散度，作为干扰的代理。

生成模型如VAEs 可以生成模糊的图像和混合类别的图像。为了在优化过程中避免这样的噪声源，我们最小化熵惩罚，以鼓励生成对前一个模型有信心的点。基于生成器的检索的最终目标是：

\\[max\\sum\\limits_z\\in\\mathbbZ[D_KLL(y_pre\\|\\haty)-\\alpha H(y_pre)]\\quad s.t.\\quad\\|z_i-z_j\\|_2^2>\\epsilon\\forall z_i,z_j\\in\\mathbbZ\\textwithz_i\\neq z_j,\\quad(2) \\]

到目前为止，我们已经假设有一个完美的编码器/解码器，我们使用它从以前的历史中检索被干扰的样本来进行被学习的函数。由于我们假设一个在线持续学习设置，我们需要解决编码器/解码器的学习.

对于分类器，我们也可以根据输入的样本和重放的样本来更新VAE。在等式中1我们只检索在分类器更新条件下会受到干扰的样本，假设是一个良好的特征表示。我们也可以使用相同的策略来减少生成器中的灾难性遗忘，通过检索受干扰最多的估计样本\\((φ,γ)\\)。在这种情况下，干扰是关于VAE的损失，明显的下界（ELBO）。让我们表示\\(γ^v\\)，\\(φ^v\\)，给定输入批处理的编码器和解码器的虚拟更新。我们考虑以下标准来检索生成器的样本：

\\[\\beginarrayl \\max _\\boldsymbolZ_\\text gen \\undersetz \\sim q_\\phi^vE\\left[-\\log \\left(p_\\gamma^v\\left(g_\\gamma^v\\left(\\boldsymbolZ_\\text gen \\right) \\mid z\\right)\\right)\\right]-\\undersetz \\sim q_\\phi^\\primeE\\left[-\\log \\left(p_\\gamma^\\prime\\left(g_\\gamma^\\prime\\left(\\boldsymbolZ_\\text gen \\right) \\mid z\\right)\\right)\\right] \\\\ +D_K L\\left(q_\\phi^v\\left(z \\mid g_\\gamma^v\\left(\\boldsymbolZ_\\text gen \\right)\\right) \\| p(z)\\right)-D_K L\\left(q_\\phi^\\prime\\left(z \\mid g_\\gamma^\\prime\\left(\\boldsymbolZ_\\text gen \\right)\\right) \\| p(z)\\right) \\\\ \\text s.t. \\quad\\left\\|z_i-z_j\\right\\|_2^2>\\epsilon \\forall z_i, z_j \\in \\boldsymbolZ_\\text gen \\text s.t. \\quad z_i \\neq z_j \\endarray \\tag 3 \\]

3.3 A Hybrid Approach

在像CIFAR- 10这样更具有挑战性的数据集上的持续学习设置中训练生成模型仍然是一个开放的研究问题。存储样本进行重放也有问题，因为它受到存储成本的限制，而且非常大的内存可能变得难以搜索。为了利用这两个方法的好处，同时避免训练噪声产生的复杂性。我们使用了一种混合的方法，即首先离线训练一个自动编码器来存储和压缩传入的内存。不同的是，在我们的方法中，我们使用等式在自动编码器的潜在空间中执行MIR搜索 .然后，我们从存储的压缩内存中选择最近的邻居，以确保真实的样本。我们的策略有几个好处：通过存储轻量级表示，缓冲区可以为相同的固定数量的内存存储更多的数据。此外，编码样本所在的特征空间是完全可微的。这使得使用梯度方法来搜索大多数受干扰的样本。我们注意到，这不是在中提出的离散自动编码器的情况。最后，具有更简单目标的自动编码器比变分自动编码器在在线设置中更容易进行训练。该方法在附录中总结为算法3。

4 Experiments

4.1 Experience Replay

由上表可以观察到加上MIR的方法，精确度上升，遗忘度下降，性能提升。

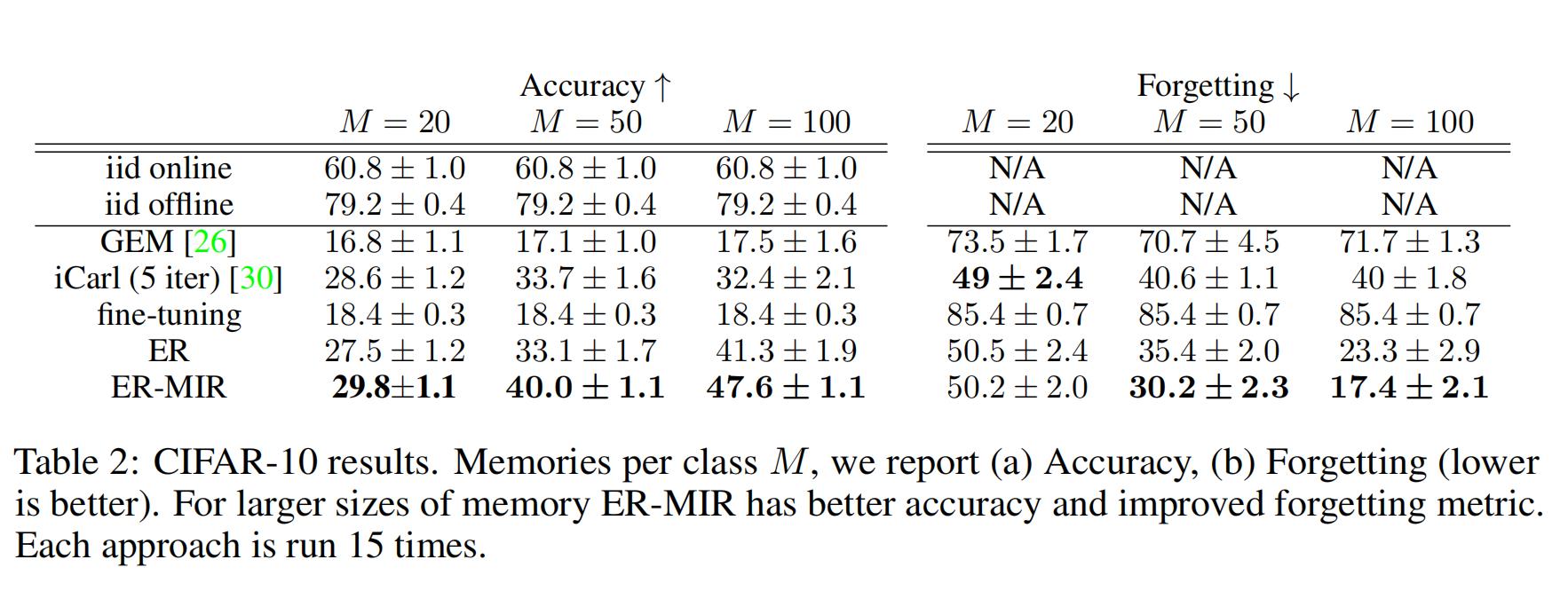
由上表可以得出内存越大，性能提升的越高

随着迭代册数的增加，性能有所提升！

ER-MIR的性能比ER的性能有所提升。

4.2 Generative Replay

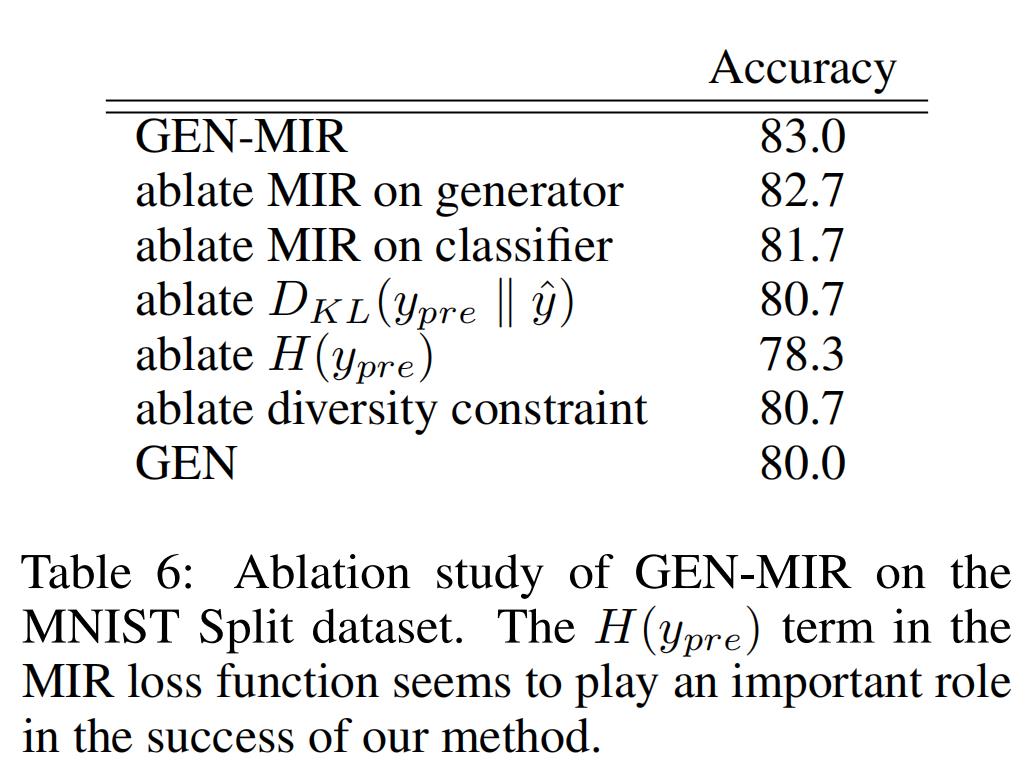
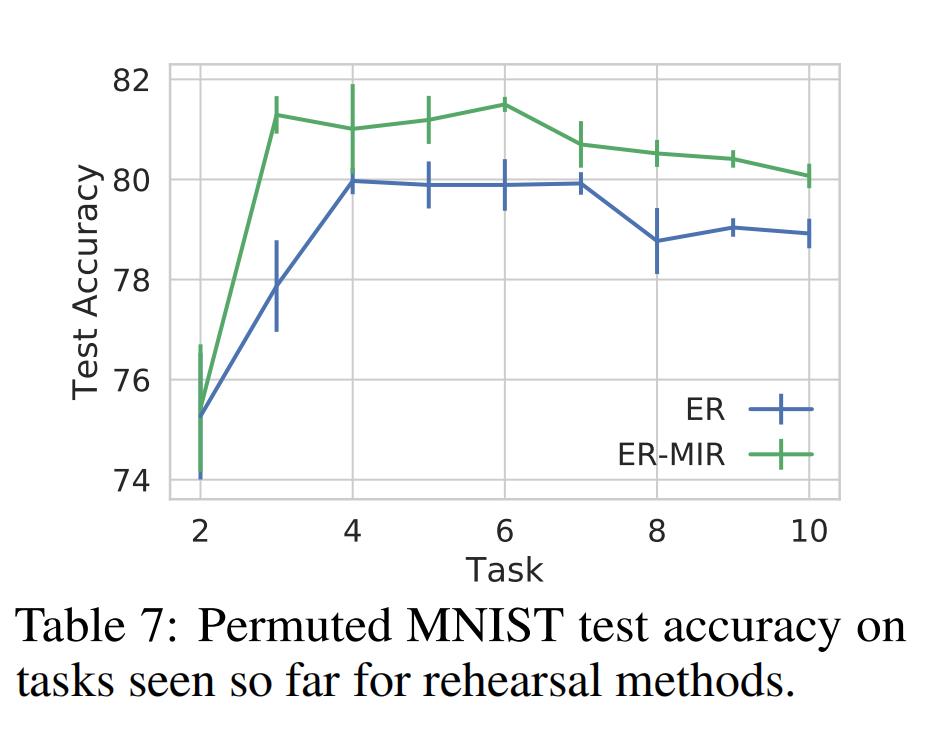
4.3 Hybrid Approach

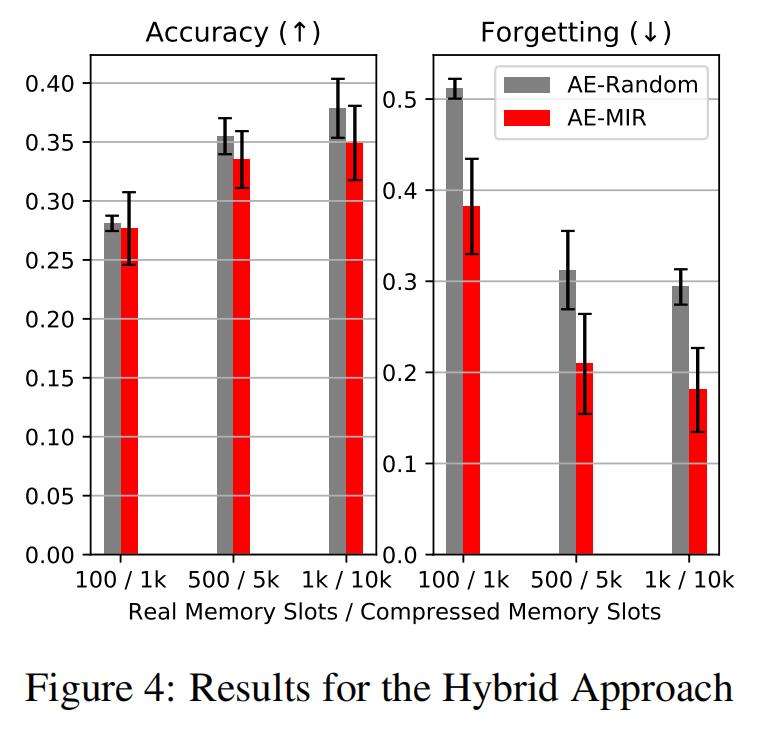
首先注意到，随着压缩样本数量的增加，我们继续看到性能的提高，这表明可以利用自动编码器获得的存储容量。我们接下来观察到，尽管AE-MIR获得了与AE-Random几乎相同的平均精度，但它在遗忘指标上实现了大幅下降，表明在学习任务的表现上有更好的权衡。

5 Conclusion

我们提出并研究了一个在在线持续学习环境中检索相关记忆的标准。我们已经在一些设置中表明，检索受干扰的样本减少了遗忘，并显著改善了随机抽样和标准基线。我们的结果和分析也阐明了在在线持续学习设置中使用生成建模的可行性和挑战。我们还展示了利用编码的记忆来实现更紧凑的记忆和更有效的检索的第一个结果。

持续学习——Continual Learning With Additive Parameter Decomposition

持续学习的概念

“持续学习”的概念其实非常好理解，正如我们先后学习高数和线代，我们希望在学习线代的时候仍能够记住之前学的高数内容，同时用高数的思想来帮助理解和学习线代，这就是一种持续学习的能力。那我们也希望神经网络可以跟人一样具备这种能力，对多个任务不断学习，而不是再为每个任务训练一个网络。这种能力概括起来就是以下两点：

• 可塑性（学习新知识的能力）：应用从之前任务学习到的经验，以更快更好地学习当前任务；
• 稳定性（旧知识的记忆能力）：学习当前任务时，不会忘记之前已经学会的任务。

持续学习面对的挑战

然鹅，传统的神经网络要实现这一目标并不容易。试想一下，我们针对某一任务训练神经网络，其实就是把从这个任务提取出来的知识以参数的形式记录在每个神经元上，而如果把这个训练好的网络拿去学习另一个任务，那所有的参数都会被覆盖，也就是说我们辛辛苦苦训练好的模型最后只变成了一套初始化参数。这就是“持续学习”中的一大难题：灾难性遗忘
除此之外，要将持续学习部署到现实世界中，还有许多问题需要解决。首先，在实际场景中，模型需要学习的任务可能很多。在“终身学习”的环境中，模型甚至需要在无限的任务上不断地训练。然而，由于“灾难性遗忘”和“关于内存的使用和计算的效率”，传统的持续学习方法对大量任务的“可扩展性”尚未得到验证。
另一个重要但相对较少研究的问题是“任务顺序敏感性”问题。由于①“灾难性遗忘”导致模型偏移以及②知识只能从前一个任务向后一任务单向转移（不能用后一任务的知识辅助训练前一任务），模型在多个任务上的训练顺序对其在每个任务上的性能存在巨大影响。如果任务之间的公平性很重要(例如疾病诊断)，这种顺序敏感性问题就不容被忽视。
综上，持续学习面对的主要挑战有三个，分别是灾难性遗忘，关于内存的使用和计算的效率，任务顺序敏感性。

Continual Learning With Additive Parameter Decomposition

针对上述问题，ICLR 2020的一篇文章《SCALABLE AND ORDER-ROBUST CONTINUAL LEARNING WITH ADDITIVE PARAMETER DECOMPOSITION》提出了一种新的持续学习方法，名为 Additive Parameter Decomposition（APD）。
APD将目标网络各层的网络参数分解为 task-shared and sparse task-specific parameters with small mask vectors。当任务每次到达带有 APD 的网络(APD - net)时，网络可以利用 task-shared parameters 进行学习，并使用 sparse task-adaptive parameters 学习 task-shared parameters 无法解释的增量差异。这里相当于把每一层模型的参数分解为 “所有任务共享的参数集” 以及“ 某一任务独有的参数集（该参数集具有稀疏性）”。
而由所有任务共享的 task-shared parameters 可能无法考虑到某几个任务间具有的一些共识知识，这将导致 sparse task-specific parameters 中存在冗余信息。文章进一步对 sparse task-adaptive parameters 进行聚类，获得 hierarchical shared parameters。
这段话举个例子就很好理解了，比如现在有三个任务 A(x, y, z)、B(x, y)、C(x, u)，括号内分别为三个任务所带有的知识，现在根据 APD，task-shared parameters 就应为 x（理想情况下为 x，实际上还可能会有 y、z、u 的一项或多项），任务 A、B、C 的 sparse task-adaptive parameters 分别为 A: (y, z), B: (y), C: (u)，可以看到，任务 A 和 B 的 sparse task-adaptive parameters 具有冗余项 y（共识知识），为了进一步减少内存占用，文章对 sparse task-adaptive parameters 进行了层次聚类。

公式化理解

带着上面的概念，我们进一步由浅入深地用公式理解 ADP。

ADP

将模型参数 θ 分解为 task-shared parameter matrix: σ 和 task-adaptive parameter matrix: τ，对于任务 t ，其模型参数 ${\theta }_t=\sigma \otimes M_t+{\tau }_t$，其中其中 mask vectors $M_t$作为 task-shared parameter 的 attention，引导学习者只关注与当前任务相关的部分。
当一个新任务到来时，可以适当地更新共享参数 σ，但不要偏离之前的共享参数 ${\sigma }^{(t-1)}$。令 ${\tau }_t$ 尽可能稀疏，以减少内存占用并提高计算效率。分解后的参数模型的目标函数如下：

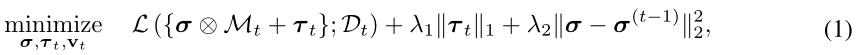
其中，L 为损失函数，$||\cdot |{|}_1$ 为 $l_1$ 范数。mask vectors $M_t$ 是一个具有可学习参数 $v_t$ 的 sigmoid 函数，该函数应用于每一层的输出通道或 σ 的神经元。
ADP 还要一个好处是，通过 task-adaptive parameter matrix 这一参数，每个任务可以有它的专属参数，模型在训练其他任务时不会改变其他任务的专属参数，这一在一定程度上缓解了“灾难性遗忘”这一问题。

Order Robust Continual Learning with Retroactive Parameter Updates

看到这里，或许有人发现虽然 task-adaptive parameter matrix 这一参数可以保持不变，但是 task-shared parameter 是随着新的任务一直在更新的呀，这不就进一步加剧了“灾难性遗忘”吗？而且还加剧了模型的“任务顺序敏感性”？是的没错，确实存在这两个问题。因此文章提出选择 “追溯更新过去任务的 task-adaptive parameter，以反映每个训练步骤的 shared parameter 的更新，使所有以前的任务都能保持原来的解。”(其实就是通过更新 task-adaptive parameter 来限制 task-shared parameter 的偏移，这不仅可以缓解“灾难性遗忘”，还可以降低模型的“任务顺序敏感性”)
公式化来讲就是，当一个新任务 t 到来时，我们先恢复所有之前的参数（${\theta }_i$ for task i < t）: ${\theta }_i^{\ast }={\sigma }^{(t-1)}\otimes M_i^{(t-1)}+{\tau }_i^{(t-1)}$，然后在限制 $\sigma \otimes M_i+{\tau }_i$ to be close to ${\theta }_i^{\ast }$ 的条件下更新 ${\tau }_{1:(t-1)}$。所以对于这个新来的任务 t ，它的目标函数为：

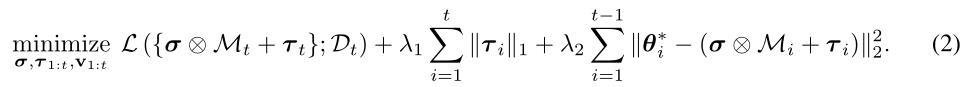
Hierarchical Knowledge Consolidation

最后一个问题就是前面提到的， task-shared parameters 可能无法考虑到某几个任务间之间的一些共识知识，进而加剧了内存占用。因此文章提出以聚类的方式来聚合这些共识知识。

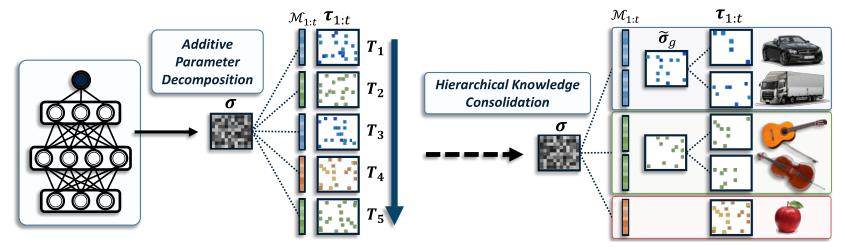
如上图所示，首先将所有任务通过 K-means 对 ${\tau }_i{}_{i=1}^t$ 进行聚类，将所有任务聚成 K 个集合 $G_g{}_{g=1}^K$，然后通过计算每个参数的 value discrepancy，将属于同一集合的任务的 task-adaptive parameters 分解成 locally-shared parameters： ${\sigma }_g$-hat 和 task-adaptive parameters：${\tau }_i{}_{i\in G_g}$ (这里的 ${\tau }_i$ 变得更加稀疏)。计算公式如下，其中 ${\tau }_{i,j}$ 代表第 i 个 task-adaptive parameter matrix 的第 j 个元素，${\mu }_g$ 是 $G_g$ 的聚类中心。
为了提高效率，每训练 s 个任务后再更新 locally-shared parameters： ${\sigma }_g$-hat，更新的方式是通过执行 K-means，以之前的 locally-shared parameters： ${\sigma }_g$-hat 为每个集合初始化聚类中心。同时需要将质心的数量增加到 K + k，以解释任务间方差的增加(随着任务数量的增多，方差必然增大，那么聚类中心肯定也得随之增加)。

final objective function and Algorithm

综上我们可以得到最终的目标函数如下：

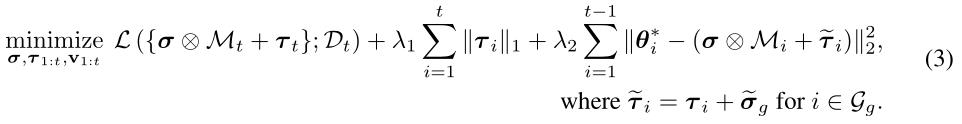
以式 (3) 作为目标函数的 ADP 持续学习伪代码如下 ：

确实🐂🍺：ADP的附加优势：Selective task forgetting

在实际场景中，随着我们不断训练模型，一些早期学习的任务可能变得无关紧要。例如，当我们在训练 “产品识别模型” 时，不再需要识别已停产的产品。在这种情况下，我们可能想要忘记之前的任务，以保证网络能够继续学习后续的任务。然而，现有的持续学习方法并不能有效地处理这个问题，因为一些特征或参数的去除也会对后面的任务产生负面影响，因为它们的参数是相互纠缠的。而在 APD 中，可以通过删除 task-adaptive parameters：${\tau }_t$来实现任务 t 的遗忘，并且，这对其余任务的 task-adaptive parameters 绝对没有影响。