DecisionTreeClassifier&DecisionTreeClassRegression

Posted 2023-04-03 Thank CAT

DecisionTreeClassifier

from sklearn.datasets import load_wine # 红酒数据集
from sklearn.tree import DecisionTreeClassifier, export_graphviz # 决策树， 画树
from sklearn.model_selection import train_test_split # 数据集划分
import graphviz
import matplotlib.pyplot as plt

# 实例化红酒数据集
wine = load_wine()

# 划分测试集和训练集
x_train, x_test, y_train, y_test = train_test_split(wine.data, wine.target, test_size=0.25)

# 实例化决策树
clf = DecisionTreeClassifier(
                            criterion="entropy"
                            ,random_state=30
                            ,splitter="random"
                            ,max_depth=4
)
clf.fit(x_train, y_train)
score = clf.score(x_test, y_test)
score

0.9333333333333333

# 查看每个特征的重要性
feature_names = [\'酒精\', \'苹果酸\', \'灰\', \'灰的碱性\', \'镁\', \'总酚\', \'类黄酮\', \'非黄烷类酚类\', \'花青素\', \'颜色强度\',\'色调\',\'od280/od315稀释葡萄酒\',\'脯氨酸\']
[*zip(feature_names, clf.feature_importances_)]

[(\'酒精\', 0.2251130582973216),
 (\'苹果酸\', 0.0),
 (\'灰\', 0.02596756412075755),
 (\'灰的碱性\', 0.0),
 (\'镁\', 0.0),
 (\'总酚\', 0.0),
 (\'类黄酮\', 0.43464628982715003),
 (\'非黄烷类酚类\', 0.03292950151904385),
 (\'花青素\', 0.02494017691000391),
 (\'颜色强度\', 0.0),
 (\'色调\', 0.03635605431269296),
 (\'od280/od315稀释葡萄酒\', 0.17795967993642653),
 (\'脯氨酸\', 0.04208767507660348)]

# 画出这棵树
data_dot = export_graphviz(
                            clf
                            ,feature_names=feature_names
                            ,class_names=["红酒","黄酒","啤酒"]
                            ,filled=True
                            ,rounded=True
)
grap = graphviz.Source(data_dot)
grap

​

​

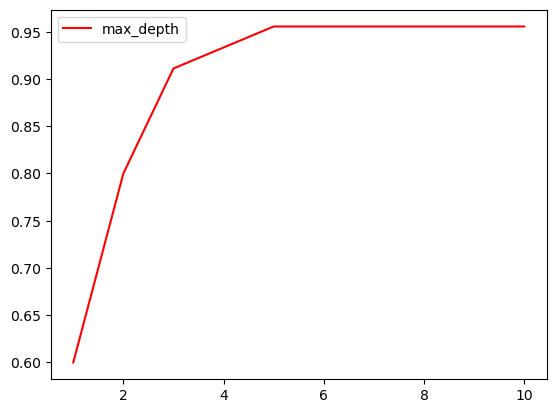
# 展示max_depth各值对准确率影响的曲线

test = []
for i in range(10):
    clf = DecisionTreeClassifier(
        criterion="entropy", random_state=30, splitter="random", max_depth=i+1
    )
    clf = clf.fit(x_train, y_train)
    score = clf.score(x_test, y_test)
    test.append(score)


plt.plot(range(1, 11),test, color="red", label="max_depth")
plt.legend()
plt.show()

​

​

DecisionTreeClassRegression

import pandas as pd # 数据处理
from sklearn.tree import DecisionTreeRegressor # 回归树
from sklearn.model_selection import cross_val_score     # 交叉验证

# 导入数据
df = pd.read_csv("./data//boston_house_prices.csv")
df.head()

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222	18.7	396.90	5.33	36.2

# 特征值
data = df.iloc[:,:-1]
data

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296	15.3	396.90	4.98
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242	17.8	396.90	9.14
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242	17.8	392.83	4.03
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222	18.7	394.63	2.94
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222	18.7	396.90	5.33
...	...	...	...	...	...	...	...	...	...	...	...	...	...
501	0.06263	0.0	11.93	0	0.573	6.593	69.1	2.4786	1	273	21.0	391.99	9.67
502	0.04527	0.0	11.93	0	0.573	6.120	76.7	2.2875	1	273	21.0	396.90	9.08
503	0.06076	0.0	11.93	0	0.573	6.976	91.0	2.1675	1	273	21.0	396.90	5.64
504	0.10959	0.0	11.93	0	0.573	6.794	89.3	2.3889	1	273	21.0	393.45	6.48
505	0.04741	0.0	11.93	0	0.573	6.030	80.8	2.5050	1	273	21.0	396.90	7.88

506 rows × 13 columns

# 目标值
target = df.iloc[:,-1:]
target

	MEDV
0	24.0
1	21.6
2	34.7
3	33.4
4	36.2
...	...
501	22.4
502	20.6
503	23.9
504	22.0
505	11.9

506 rows × 1 columns

# 实例化回归树
clr = DecisionTreeRegressor(random_state=0)

# 实例化交叉验证
cross = cross_val_score(clr, data, target, scoring="neg_mean_squared_error", cv=10)
cross

array([-18.08941176, -10.61843137, -16.31843137, -44.97803922,
       -17.12509804, -49.71509804, -12.9986    , -88.4514    ,
       -55.7914    , -25.0816    ])

一维回归图像绘制

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

rng = np.random.RandomState(1)
rng

RandomState(MT19937) at 0x7FC5EEAAAF40

x = np.sort(5 * rng.rand(80,1), axis=0)
x

array([[5.71874087e-04],
       [9.14413867e-02],
       [9.68347894e-02],
       [1.36937966e-01],
       [1.95273916e-01],
       [2.49767295e-01],
       [2.66812726e-01],
       [4.25221057e-01],
       [4.61692974e-01],
       [4.91734169e-01],
       [5.11672144e-01],
       [5.16130033e-01],
       [6.50142861e-01],
       [6.87373521e-01],
       [6.96381736e-01],
       [7.01934693e-01],
       [7.33642875e-01],
       [7.33779454e-01],
       [8.26770986e-01],
       [8.49152098e-01],
       [9.31301057e-01],
       [9.90507445e-01],
       [1.02226125e+00],
       [1.05814058e+00],
       [1.32773330e+00],
       [1.40221996e+00],
       [1.43887669e+00],
       [1.46807074e+00],
       [1.51166286e+00],
       [1.56712089e+00],
       [1.57757816e+00],
       [1.72780364e+00],
       [1.73882930e+00],
       [1.98383737e+00],
       [1.98838418e+00],
       [2.07027994e+00],
       [2.07089635e+00],
       [2.08511002e+00],
       [2.08652401e+00],
       [2.09597257e+00],
       [2.10553813e+00],
       [2.23946763e+00],
       [2.45786580e+00],
       [2.57444556e+00],
       [2.66582642e+00],
       [2.67948203e+00],
       [2.69408367e+00],
       [2.79344914e+00],
       [2.87058803e+00],
       [2.93277520e+00],
       [2.94652768e+00],
       [3.31897323e+00],
       [3.35233755e+00],
       [3.39417766e+00],
       [3.42609750e+00],
       [3.43250464e+00],
       [3.45938557e+00],
       [3.46161308e+00],
       [3.47200079e+00],
       [3.49879180e+00],
       [3.60162247e+00],
       [3.62998993e+00],
       [3.74082827e+00],
       [3.75072157e+00],
       [3.75406052e+00],
       [3.94639664e+00],
       [4.00372284e+00],
       [4.03695644e+00],
       [4.17312836e+00],
       [4.38194576e+00],
       [4.39058718e+00],
       [4.39071252e+00],
       [4.47303332e+00],
       [4.51700958e+00],
       [4.54297752e+00],
       [4.63754290e+00],
       [4.72297378e+00],
       [4.78944765e+00],
       [4.84130788e+00],
       [4.94430544e+00]])

y = np.sin(x).ravel()

y[::5] += 3 * (0.5 - rng.rand(16))
y

array([-1.1493464 ,  0.09131401,  0.09668352,  0.13651039,  0.19403525,
       -0.12383814,  0.26365828,  0.41252216,  0.44546446,  0.47215529,
       -0.26319138,  0.49351799,  0.60530013,  0.63450933,  0.64144608,
        1.09900119,  0.66957978,  0.66968122,  0.73574834,  0.75072053,
        1.4926134 ,  0.8363043 ,  0.8532893 ,  0.87144496,  0.97060533,
       -0.20183403,  0.99131122,  0.99472837,  0.99825213,  0.99999325,
        1.21570343,  0.98769965,  0.98591565,  0.9159044 ,  0.91406986,
       -0.51669013,  0.8775346 ,  0.87063055,  0.86993408,  0.86523559,
        0.37007575,  0.78464608,  0.63168655,  0.53722799,  0.45801971,
        0.08075119,  0.43272116,  0.34115328,  0.26769953,  0.20730318,
        1.34959235, -0.17645185, -0.20918837, -0.24990778, -0.28068224,
       -1.63529379, -0.31247075, -0.31458595, -0.32442911, -0.34965155,
       -0.29371122, -0.46921115, -0.56401144, -0.57215326, -0.57488849,
       -0.95586361, -0.75923066, -0.78043659, -0.85808859, -0.94589863,
       -0.6730775 , -0.94870673, -0.97149093, -0.98097408, -0.98568417,
       -0.20828128, -0.99994398, -0.99703245, -0.99170146, -0.9732277 ])

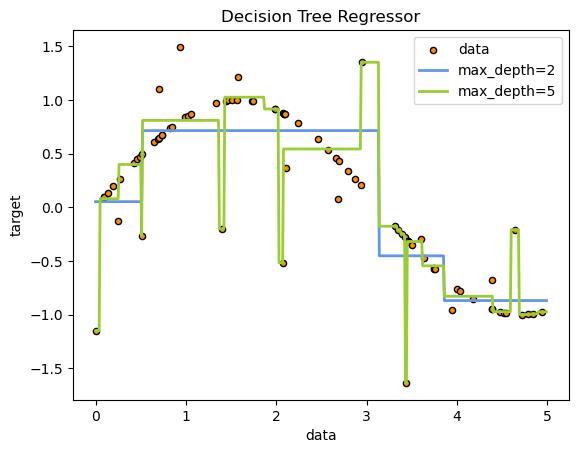
reg1 = DecisionTreeRegressor(max_depth=2)
reg2 = DecisionTreeRegressor(max_depth=5)
reg1.fit(x, y)
reg2.fit(x, y)

DecisionTreeRegressor(max_depth=5)

x_test = np.arange(0.0, 5.0, 0.01)[:,np.newaxis]
x_test

array([[0.  ],
       [0.01],
       [0.02],
       [0.03],
       [0.04],
       [0.05],
       [0.06],
       [0.07],
       [0.08],
       [0.09],
       [0.1 ],
       [0.11],
       [0.12],
       [0.13],
       [0.14],
       [0.15],
       [0.16],
       [0.17],
       [0.18],
       [0.19],
       [0.2 ],
       [0.21],
       [0.22],
       [0.23],
       [0.24],
       [0.25],
       [0.26],
       [0.27],
       [0.28],
       [0.29],
       [0.3 ],
       [0.31],
       [0.32],
       [0.33],
       [0.34],
       [0.35],
       [0.36],
       [0.37],
       [0.38],
       [0.39],
       [0.4 ],
       [0.41],
       [0.42],
       [0.43],
       [0.44],
       [0.45],
       [0.46],
       [0.47],
       [0.48],
       [0.49],
       [0.5 ],
       [0.51],
       [0.52],
       [0.53],
       [0.54],
       [0.55],
       [0.56],
       [0.57],
       [0.58],
       [0.59],
       [0.6 ],
       [0.61],
       [0.62],
       [0.63],
       [0.64],
       [0.65],
       [0.66],
       [0.67],
       [0.68],
       [0.69],
       [0.7 ],
       [0.71],
       [0.72],
       [0.73],
       [0.74],
       [0.75],
       [0.76],
       [0.77],
       [0.78],
       [0.79],
       [0.8 ],
       [0.81],
       [0.82],
       [0.83],
       [0.84],
       [0.85],
       [0.86],
       [0.87],
       [0.88],
       [0.89],
       [0.9 ],
       [0.91],
       [0.92],
       [0.93],
       [0.94],
       [0.95],
       [0.96],
       [0.97],
       [0.98],
       [0.99],
       [1.  ],
       [1.01],
       [1.02],
       [1.03],
       [1.04],
       [1.05],
       [1.06],
       [1.07],
       [1.08],
       [1.09],
       [1.1 ],
       [1.11],
       [1.12],
       [1.13],
       [1.14],
       [1.15],
       [1.16],
       [1.17],
       [1.18],
       [1.19],
       [1.2 ],
       [1.21],
       [1.22],
       [1.23],
       [1.24],
       [1.25],
       [1.26],
       [1.27],
       [1.28],
       [1.29],
       [1.3 ],
       [1.31],
       [1.32],
       [1.33],
       [1.34],
       [1.35],
       [1.36],
       [1.37],
       [1.38],
       [1.39],
       [1.4 ],
       [1.41],
       [1.42],
       [1.43],
       [1.44],
       [1.45],
       [1.46],
       [1.47],
       [1.48],
       [1.49],
       [1.5 ],
       [1.51],
       [1.52],
       [1.53],
       [1.54],
       [1.55],
       [1.56],
       [1.57],
       [1.58],
       [1.59],
       [1.6 ],
       [1.61],
       [1.62],
       [1.63],
       [1.64],
       [1.65],
       [1.66],
       [1.67],
       [1.68],
       [1.69],
       [1.7 ],
       [1.71],
       [1.72],
       [1.73],
       [1.74],
       [1.75],
       [1.76],
       [1.77],
       [1.78],
       [1.79],
       [1.8 ],
       [1.81],
       [1.82],
       [1.83],
       [1.84],
       [1.85],
       [1.86],
       [1.87],
       [1.88],
       [1.89],
       [1.9 ],
       [1.91],
       [1.92],
       [1.93],
       [1.94],
       [1.95],
       [1.96],
       [1.97],
       [1.98],
       [1.99],
       [2.  ],
       [2.01],
       [2.02],
       [2.03],
       [2.04],
       [2.05],
       [2.06],
       [2.07],
       [2.08],
       [2.09],
       [2.1 ],
       [2.11],
       [2.12],
       [2.13],
       [2.14],
       [2.15],
       [2.16],
       [2.17],
       [2.18],
       [2.19],
       [2.2 ],
       [2.21],
       [2.22],
       [2.23],
       [2.24],
       [2.25],
       [2.26],
       [2.27],
       [2.28],
       [2.29],
       [2.3 ],
       [2.31],
       [2.32],
       [2.33],
       [2.34],
       [2.35],
       [2.36],
       [2.37],
       [2.38],
       [2.39],
       [2.4 ],
       [2.41],
       [2.42],
       [2.43],
       [2.44],
       [2.45],
       [2.46],
       [2.47],
       [2.48],
       [2.49],
       [2.5 ],
       [2.51],
       [2.52],
       [2.53],
       [2.54],
       [2.55],
       [2.56],
       [2.57],
       [2.58],
       [2.59],
       [2.6 ],
       [2.61],
       [2.62],
       [2.63],
       [2.64],
       [2.65],
       [2.66],
       [2.67],
       [2.68],
       [2.69],
       [2.7 ],
       [2.71],
       [2.72],
       [2.73],
       [2.74],
       [2.75],
       [2.76],
       [2.77],
       [2.78],
       [2.79],
       [2.8 ],
       [2.81],
       [2.82],
       [2.83],
       [2.84],
       [2.85],
       [2.86],
       [2.87],
       [2.88],
       [2.89],
       [2.9 ],
       [2.91],
       [2.92],
       [2.93],
       [2.94],
       [2.95],
       [2.96],
       [2.97],
       [2.98],
       [2.99],
       [3.  ],
       [3.01],
       [3.02],
       [3.03],
       [3.04],
       [3.05],
       [3.06],
       [3.07],
       [3.08],
       [3.09],
       [3.1 ],
       [3.11],
       [3.12],
       [3.13],
       [3.14],
       [3.15],
       [3.16],
       [3.17],
       [3.18],
       [3.19],
       [3.2 ],
       [3.21],
       [3.22],
       [3.23],
       [3.24],
       [3.25],
       [3.26],
       [3.27],
       [3.28],
       [3.29],
       [3.3 ],
       [3.31],
       [3.32],
       [3.33],
       [3.34],
       [3.35],
       [3.36],
       [3.37],
       [3.38],
       [3.39],
       [3.4 ],
       [3.41],
       [3.42],
       [3.43],
       [3.44],
       [3.45],
       [3.46],
       [3.47],
       [3.48],
       [3.49],
       [3.5 ],
       [3.51],
       [3.52],
       [3.53],
       [3.54],
       [3.55],
       [3.56],
       [3.57],
       [3.58],
       [3.59],
       [3.6 ],
       [3.61],
       [3.62],
       [3.63],
       [3.64],
       [3.65],
       [3.66],
       [3.67],
       [3.68],
       [3.69],
       [3.7 ],
       [3.71],
       [3.72],
       [3.73],
       [3.74],
       [3.75],
       [3.76],
       [3.77],
       [3.78],
       [3.79],
       [3.8 ],
       [3.81],
       [3.82],
       [3.83],
       [3.84],
       [3.85],
       [3.86],
       [3.87],
       [3.88],
       [3.89],
       [3.9 ],
       [3.91],
       [3.92],
       [3.93],
       [3.94],
       [3.95],
       [3.96],
       [3.97],
       [3.98],
       [3.99],
       [4.  ],
       [4.01],
       [4.02],
       [4.03],
       [4.04],
       [4.05],
       [4.06],
       [4.07],
       [4.08],
       [4.09],
       [4.1 ],
       [4.11],
       [4.12],
       [4.13],
       [4.14],
       [4.15],
       [4.16],
       [4.17],
       [4.18],
       [4.19],
       [4.2 ],
       [4.21],
       [4.22],
       [4.23],
       [4.24],
       [4.25],
       [4.26],
       [4.27],
       [4.28],
       [4.29],
       [4.3 ],
       [4.31],
       [4.32],
       [4.33],
       [4.34],
       [4.35],
       [4.36],
       [4.37],
       [4.38],
       [4.39],
       [4.4 ],
       [4.41],
       [4.42],
       [4.43],
       [4.44],
       [4.45],
       [4.46],
       [4.47],
       [4.48],
       [4.49],
       [4.5 ],
       [4.51],
       [4.52],
       [4.53],
       [4.54],
       [4.55],
       [4.56],
       [4.57],
       [4.58],
       [4.59],
       [4.6 ],
       [4.61],
       [4.62],
       [4.63],
       [4.64],
       [4.65],
       [4.66],
       [4.67],
       [4.68],
       [4.69],
       [4.7 ],
       [4.71],
       [4.72],
       [4.73],
       [4.74],
       [4.75],
       [4.76],
       [4.77],
       [4.78],
       [4.79],
       [4.8 ],
       [4.81],
       [4.82],
       [4.83],
       [4.84],
       [4.85],
       [4.86],
       [4.87],
       [4.88],
       [4.89],
       [4.9 ],
       [4.91],
       [4.92],
       [4.93],
       [4.94],
       [4.95],
       [4.96],
       [4.97],
       [4.98],
       [4.99]])

y1 = reg1.predict(x_test)
y2 = reg2.predict(x_test)

plt.figure()
plt.scatter(x,y,s=20, edgecolors="black", c="darkorange", label="data")
plt.plot(x_test, y1, color="cornflowerblue",label="max_depth=2",linewidth=2)
plt.plot(x_test, y2, color="yellowgreen",label="max_depth=5",linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regressor")
plt.legend()
plt.show()

​

​

处理 sklearn.tree.DecisionTreeClassifier 中的连续变量

【中文标题】处理 sklearn.tree.DecisionTreeClassifier 中的连续变量

【英文标题】：Handle continuous variables in sklearn.tree.DecisionTreeClassifier

【发布时间】：2020-04-01 12:56:22

【问题描述】：

我很好奇sklearn 是如何处理sklearn.tree.DecisionTreeClassifier 中的连续变量的？我尝试使用一些连续变量而不使用 DecisionTreeClassifier 进行预处理，但它得到了可以接受的准确度。

下面是一种将连续变量转化为分类变量的方法，但不能得到同样的准确度。

def preprocess(data, min_d, max_d, bin_size=3):

    norm_data = np.clip((data - min_d) / (max_d - min_d), 0, 1)
    categorical_data = np.floor(bin_size*norm_data).astype(int)
    return categorical_data


X = preprocess(X, X.min(), X.max(), 3)

【参考方案1】：

决策树在最能区分两个类的位置拆分连续值。例如，假设一棵决策树将男性和女性的身高划分为 165 厘米，因为大多数人都可以根据这个边界正确分类。一个算法会发现，大多数女性都在 165cm 以下，而大多数男性则超过 165cm。

决策树会找到所有属性的最佳分裂点，通常会多次重用属性。请参见此处，根据列中的连续值对 Iris 数据集进行分类的决策树。

例如，您可以看到X[3] < 0.8，其中某些列中低于 0.8 的连续值被归类为 0 类。您可以看到这种拆分适用于每个类中的实例数：[50, 0, 0]。

您的任意分割点的准确性可能较低，因为这样做会丢失信息。关于身高的例子，想象一下如果你的身高数据不是连续的，但是你有超过 150 厘米和低于 150 厘米的人。你会丢失很多信息。决策树也会像这样拆分连续数据，但至少它会 1）找到最佳拆分点，以及 2）它将能够多次拆分相同的属性。所以它会比你的任意拆分表现更好。

【讨论】：

谢谢！但我这里还有一个问题：决策树如何找到the place？如果值是连续的，则有无数个可能的地方最能区分这两个类。

是的，有。这就是优化算法发挥作用的时候，例如CART algorithm。