如何分析回溯 dfs时间复杂度

Posted 2023-04-02

参考技术A 因为是选择其中一个方向不断前进，直接遇到某条件后才返回到上一次的起点重新尝试另一条路径。如果是广度优先，那么应该是同时向多个方向进发。

DFS ( 深度优先/回溯算法 ) 一

    深度优先搜索算法（英语：Depth-First-Search，简称DFS）是一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。（Wiki）

   DFS在搜索过程常常伴随许多优化策略，增加剪枝函数，或者和动态规划结合。

   让我们用一道看似简单的例子理解DFS。 = =

 

/*
**  将一个整数n分为k个加数相加，不能重复。e.g. n=7 k=2 -> (1,6) (2,5) (3,4)  // (4,3)等为重复项
**  求有多少种分法，并打印每种分法
**  0<n<=200 1<k<=7
*/


#include <iostream>

using namespace std;
int sum = 0;
int finalExp[8];

void numDivision(int num,int parts,int curr = 1,int level = 1)
{
    if ( parts == 1 ){   //搜寻结点到达末尾的条件
           sum++; //获得一种分法
           int s = 0;
           int i;
            for ( i = 1; i < level; i++ ){
                    s += finalExp[i];
                cout << finalExp[i] << " + ";
            }
            cout << num << " = " << num+s << endl;
            return ;
    }
    for ( int i = curr; i <= num/parts; i++ ){
         finalExp[level] = i;                   //储存结果
         numDivision(num-i,parts-1,i,level+1);      //核心回溯递归
    }
}

int main()
{
    numDivision(7,3);

    cout << sum << endl;

    return 0;
}  // Achieve 

 

    例子显示的正是多数DFS通用的框架。

                int arr[]   // 解集

                dfs() {

                         if (){  //搜寻是否到达末尾

                              //解集操作

                          }

                        if(){     //或者为 for() , while()

                                dfs()  //判断后回溯递归

                         }

               }

      难点在于分析问题时，如何获取搜寻结点的终结条件，应怎样改变递归的参数.....

      回溯算法如百科所言是一种用于遍历或搜索树的算法。我们可以将问题分解绘成树状结构。

      

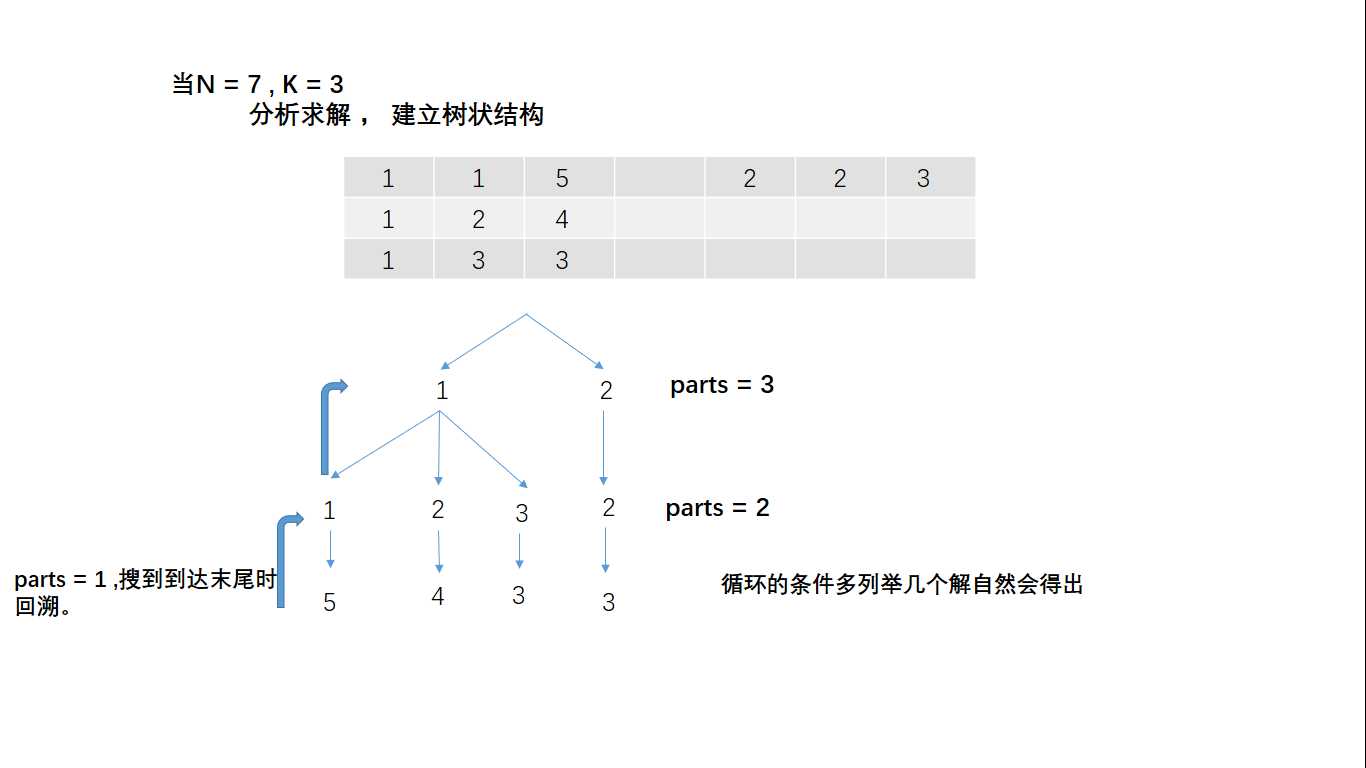
     DFS的简单演示时间结束~  希望对你有帮助。