进制转化复习（ 万能的a进制转化为b进制）

Posted 2023-04-01 sdnu-dfl

进制转化复习

十进制转化为十六进制

Description

　　十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号，分别表示十进制数的0至15。十六进制的计数方法是满16进1，所以十进制数16在十六进制中是10，而十进制的17在十六进制中是11，以此类推，十进制的30在十六进制中是1E。
　　给出一个非负整数，将它表示成十六进制的形式。

Input

输入描述:
　　输入包含一个非负整数a，表示要转换的数。0<=a<=2147483647
输入样例:
30

Output

输出描述:
　　输出这个整数的16进制表示
输出样例:
1E

---

#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int a[N];
int n;
int cnt;
int main()

	cin>>n;
	
	char b[]=\'0\',\'1\',\'2\',\'3\',\'4\',\'5\',\'6\',\'7\',\'8\',\'9\',\'A\',\'B\',\'C\',\'D\',\'E\',\'F\';
	
	do
	
		a[cnt++]=n%16;
		n/=16;
	while (n);
	
	for (int i=cnt-1;i>=0;i--)
	
		int index = a[i];
		cout<<b[index];
	
	puts("");
	return 0;

---

十进制转化为二进制（除留余数法）

#include <bits/stdc++.h>
using namespace std;
const int N = 35;
int n;
int a[N];
int cnt;
int main()

	cin>>n;
	
	do
		a[cnt++]=n%2;
		n/=2;
	 while (n);
	
	for (int i=cnt-1;i>=0;i--)
		cout<<a[i];
	puts("");
	return 0;

十六进制转化为十进制

#include <bits/stdc++.h>
using namespace std;
int main()

	
		string a_line,b_line;
		cin>>a_line;
		vector<int>num;
		for (auto c:a_line)
		
		    if (c>=\'A\'&&c<=\'F\') num.push_back(c-\'A\'+10);
		    else num.push_back(c-\'0\');
		
		
		reverse(num.begin(),num.end());
		vector<int>ans;
		while (num.size())
		
			int r=0;
			for (int i=num.size()-1;i>=0;i--)
			
				num[i]+=r*16;
				r=num[i]%10;
				num[i]/=10;
			
			ans.push_back(r);
			while (num.size()&&num.back()==0) num.pop_back();
		
		
		reverse(ans.begin(),ans.end());
		for (auto x:ans) cout<<x;
		cout<<endl;
	return 0;

---

a进制转化为b进制

编写一个程序，可以实现将一个数字由一个进制转换为另一个进制。

这里有 $ 62 $ 个不同数位 $ 0-9,A-Z,a-z $。

输入格式

第一行输入一个整数，代表接下来的行数。

接下来每一行都包含三个数字，首先是输入进制（十进制表示），然后是输出进制（十进制表示），最后是用输入进制表示的输入数字，数字之间用空格隔开。

输入进制和输出进制都在 $ 2 $ 到 $ 62 $ 的范围之内。

（在十进制下）$ A = 10，B = 11，…，Z = 35，a = 36，b = 37，…，z = 61 $ ($ 0-9 $ 仍然表示 $ 0-9 $)。

输出格式

对于每一组进制转换，程序的输出都由三行构成。

第一行包含两个数字，首先是输入进制（十进制表示），然后是用输入进制表示的输入数字。

第二行包含两个数字，首先是输出进制（十进制表示），然后是用输出进制表示的输入数字。

第三行为空白行。

同一行内数字用空格隔开。

输入样例：

8
62 2 abcdefghiz
10 16 1234567890123456789012345678901234567890
16 35 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2
35 23 333YMHOUE8JPLT7OX6K9FYCQ8A
23 49 946B9AA02MI37E3D3MMJ4G7BL2F05
49 61 1VbDkSIMJL3JjRgAdlUfcaWj
61 5 dl9MDSWqwHjDnToKcsWE1S
5 10 42104444441001414401221302402201233340311104212022133030

输出样例：

62 abcdefghiz
2 11011100000100010111110010010110011111001001100011010010001

10 1234567890123456789012345678901234567890
16 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2

16 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2
35 333YMHOUE8JPLT7OX6K9FYCQ8A

35 333YMHOUE8JPLT7OX6K9FYCQ8A
23 946B9AA02MI37E3D3MMJ4G7BL2F05

23 946B9AA02MI37E3D3MMJ4G7BL2F05
49 1VbDkSIMJL3JjRgAdlUfcaWj

49 1VbDkSIMJL3JjRgAdlUfcaWj
61 dl9MDSWqwHjDnToKcsWE1S

61 dl9MDSWqwHjDnToKcsWE1S
5 42104444441001414401221302402201233340311104212022133030

5 42104444441001414401221302402201233340311104212022133030
10 1234567890123456789012345678901234567890

#include<bits/stdc++.h>
using namespace std;
int main()

    ios;
    int T;  //输入样例的个数
    cin >> T;
    while(T--)
    
        //读入
        ios;
        int a,b;
        string a_line,b_line;

        cin >> a >> b>>a_line;  //由a进制转换成b进制 

        vector<int> number;     //number来存储由str转换成10进制的数据
        for(auto c : a_line)
        
            if(c>=\'0\' && c<=\'9\') number.push_back(c-\'0\');     //str转int形数据，因为无需根据偏移量转换，所以是减去0
            if(c>=\'A\' && c<=\'Z\') number.push_back(c-\'A\'+10);  //通过与A的偏移量来进行转换
            if(c>=\'a\' && c<=\'z\') number.push_back(c-\'a\'+36);  //减去0到9和大写的26个英文字母的偏移量
        
        reverse(number.begin(),number.end());   //存储时我们是把高位放在了下标为0的位置，y总习惯从低位到高位存，使位数和数组的下标一致

        vector<int> res;     
        while(number.size()) //numberz只要没被除成0就一直做 
        
            int r = 0;      //余数
            for(int i = number.size() - 1; i >= 0; i--)
            
                number[i] += r * a; // 当前这一位的值 是 ：当前这一位的值 + 上一位的借位 * a  (因为一开始是a进制的，所以需要乘以a)
                r = number[i] % b;  //每一位再对b取余得到每一位
                number[i] /= b;  // 商的位 是number的位整除b的结果 
            
            res.push_back(r); //最后的余数就是我现在的个位

            while(number.size() && number.back() == 0/*!number.back()*/) number.pop_back();   //删去前导0
        

        reverse(res.begin(),res.end());  //因为短除法是push_back()的次序是 从上到下 的每一次余数，
                                            //但是我们输出的时候要逆序输出，所以再reverse一次
        for (auto x : res)  //如果是10进制以内的转换 我们直接输出就可以了现在，但是 这儿最高是62进制 要再进行一个转换!
        
            if (x <= 9)                 b_line += char(x + \'0\');
            if (x >= 10 && x <= 35)     b_line += char(x + \'A\' - 10);
            if (x >= 36)                b_line += char(x + \'a\' - 36);
        
        cout << a << \' \' << a_line << endl;
        cout << b << \' \' << b_line << endl;
        cout << endl;
    
    return 0;

如何将数值转化为二进制数？

参考技术A

小数转化为二进制数的方法：

1、十进制的小数转换为二进制，主要是小数部分乘以2，取整数部分依次从左往右放在小数点后，直至小数点后为0。例如十进制的0.125，要转换为二进制的小数。

2、转换为二进制，将小数部分0.125乘以2，得0.25，然后取整数部分0。

3、再将小数部分0.25乘以2，得0.5，然后取整数部分0。

4、再将小数部分0.5乘以2，得1，然后取整数部分1。

5、则得到的二进制的结果就是0.001。

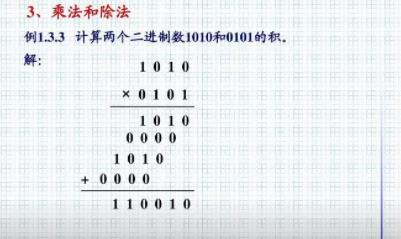
计数系统

进制

在基数b的位置记数系统(其中b是一个正自然数，叫做基数)，b个基本符号(或者叫数字)对应于包括0的最小b个自然数。要产生其他的数，符号在数中的位置要被用到。最后一位的符号用它本身的值，向左一位其值乘以b。

二进制计数

17世纪至18世纪的德国数学家莱布尼茨，是世界上第一个提出二进制记数法的人。用二进制记数，只用0和1两个符号，无需其他符号。