Leetcode Practice --- 栈和队列
Posted iSherryZhang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Leetcode Practice --- 栈和队列相关的知识,希望对你有一定的参考价值。
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。
提示:
-
\\(-2^31\\) <= val <= \\(2^31\\) - 1
-
pop、top 和 getMin 操作总是在 非空栈 上调用
-
push, pop, top, and getMin最多被调用 \\(3 * 10^4\\) 次
-
思路解析
因为会不断的入栈和出栈,那就要保证,不论入栈还是出栈,我时刻知道,到栈中当前位置的最小值是谁。
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
对于上述输入,-2入栈时,最小值是-2,0入栈是,最小值是-2,-3入栈是最小值是-3
也就是我需要两个栈,一个栈用于存储元素,完成元素的push和pop操作;一个栈用于存储当前最小值,如果最小值更新就存入最小栈。
class MinStack
public:
MinStack()
void push(int val)
if (val <= getMin())
minStack.emplace(val);
valStack.emplace(val);
void pop()
if (valStack.empty())
return;
int ret = valStack.top();
valStack.pop();
if (ret == getMin())
minStack.pop();
int top()
return valStack.top();
int getMin()
if (minStack.empty())
return INT_MAX;
return minStack.top();
private:
stack<int> valStack;
stack<int> minStack;
;
20. 有效的括号
给定一个只包括 \'(\',\')\',\'\',\'\',\'[\',\']\' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
-
左括号必须用相同类型的右括号闭合。
-
左括号必须以正确的顺序闭合。
-
每个右括号都有一个对应的相同类型的左括号。
-
思路解析
将匹配项做一个map单独存储,这样子有更好的扩展性。
遇到左括号就入栈,遇到右括号,判断是否与栈顶元素配对,配上就出栈,否则就返回false。
class Solution
public:
bool isValid(string s)
stack<char> bracketsStack;
for (auto &iter : s)
// 遇到左括号就入栈,遇到右括号,判断栈顶是否为其对应的左括号,如果是则出栈
if (typeMap.count(iter) != 0)
bracketsStack.emplace(iter);
else
if (bracketsStack.empty() || iter != typeMap[bracketsStack.top()])
return false;
bracketsStack.pop();
if (bracketsStack.empty())
return true;
return false;
private:
unordered_map<char, char> typeMap =
\'(\', \')\',
\'[\', \']\',
\'\', \'\'
;
;
1047. 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
输入:"abbaca"
输出:"ca"
输入:"abbbaca"
输出:"abaca"
-
思路解析
string提供了两个操作
- front:访问第一个字符
- back:查询最后一个字符
- pop_back:弹出尾巴字符,实现:length - 1即可
- push_back:插入元素
string removeDuplicates(string s)
string res;
for (auto &iter : s)
if (!res.empty() && iter == res.back())
res.pop_back();
else
res.push_back(iter);
return res;
1209. 删除字符串中的所有相邻重复项 II
给你一个字符串 s,「k 倍重复项删除操作」将会从 s 中选择 k 个相邻且相等的字母,并删除它们,使被删去的字符串的左侧和右侧连在一起。
你需要对 s 重复进行无限次这样的删除操作,直到无法继续为止。
在执行完所有删除操作后,返回最终得到的字符串。
输入:s = "deeedbbcccbdaa", k = 3
输出:"aa"
解释:
先删除 "eee" 和 "ccc",得到 "ddbbbdaa"
再删除 "bbb",得到 "dddaa"
最后删除 "ddd",得到 "aa"
-
思路解析
遍历到某个字符的时候,判断当前字符与栈顶字符是否相同
- 如果不同,则直接入栈并开始计数
- 如果相同,则判断当前栈顶元素累积了多少个该元素,如果累积的个数小于k-1,则继续累积,如果累积到了k-1个,当前又相同了,那么栈顶元素就可以弹出了。
string removeDuplicates(string s, int k)
stack<std::pair<char, int>> pairStack; // 每个元素存储当前的元素及有几个连续的值
for (size_t i = 0; i < s.length(); i++)
if (!pairStack.empty() && pairStack.top().first == s[i])
// 此时,看一下栈中是否已经有k-1个s[i]相同的元素,如果有,则pop出这k-1个,如果没有,则push进去
if (pairStack.top().second == k - 1)
pairStack.pop();
else
pairStack.top().second++;
else
pairStack.emplace(std::pair<char, int>(s[i], 1));
string res;
while(!pairStack.empty())
while (pairStack.top().second-- > 0)
res += pairStack.top().first;
pairStack.pop();
reverse(res.begin(), res.end());
return res;
删除字符串中出现次数 >= 2 次的相邻字符
第二次出现的时候,说明出现次数大于2了,这时候就可以删除了,同时跳过s中后续与当前字符相同的元素即可。
string removeDuplicates(string s, int k)
string res; // 每个元素存储当前的元素及有几个连续的值
for (size_t i = 0; i < s.length(); )
if (!res.empty() && res.back() == s[i])
// 此时,说明已经出现过的字符第二次出现了
char currChar = s[i];
while(s[i] == currChar)
// 跳过s中其他相同的字符
i++;
res.pop_back();
else
res.push_back(s[i]);
i++;
return res;
剑指 Offer 09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
class CQueue
public:
CQueue()
void appendTail(int value)
stackIn.emplace(value);
int deleteHead()
if (stackOut.empty())
while (!stackIn.empty())
stackOut.emplace(stackIn.top());
stackIn.pop();
if (stackOut.empty())
return -1;
auto ret = stackOut.top();
stackOut.pop();
return ret;
private:
stack<int> stackOut; // 输出栈,元素按照输入顺序的栈
stack<int> stackIn; // 输入元素存放栈,与输入顺序相反的栈
;
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回 滑动窗口中的最大值 。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
-
思路解析
假设窗口为[left, right],那么只要nums[i]比nums[j]小,则nums[i]就不纳入考虑范围。所以,当right进入窗口的时候,前面比nums[right]小的元素统统可以移除考虑范围了;这样子,留下的元素是从大到小有序的。
因为我们要移除比当前元素小的元素,也要获取最大的元素作为当前窗口最大值,因此,可以使用双端队列来实现。
// 移除比当前元素小的所有元素,只留下比当前元素大的元素
while (!dQ.empty() && nums[i] >= nums[dQ.back()])
dQ.pop_back();
// 获取当前窗口最大值,放入结果中
resVec.emplace_back(nums[dQ.front()]);
// 如果最大值应该要移除了,则移除
if (dQ.front() + k <= i)
dQ.pop_front();
完整的实现代码如下:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
deque<int> dQ;
for (size_t i = 0; i < k; i++)
// 当前队列中仅保留比当前元素大的元素的位置,队列中下标对应的元素由大到小
while (!dQ.empty() && nums[i] >= nums[dQ.back()])
dQ.pop_back();
dQ.emplace_back(i);
vector<int> resVec = nums[dQ.front()];
for (size_t i = k; i < nums.size(); i++)
// 当前队列中仅保留比当前元素大的元素的位置
while (!dQ.empty() && nums[i] >= nums[dQ.back()])
dQ.pop_back();
dQ.emplace_back(i);
if (dQ.front() <= i - k)
dQ.pop_front();
resVec.emplace_back(nums[dQ.front()]);
return resVec;
需要完整版练习笔记,可关注公众号后台私信~~

关注我的公众号 不定期推送资讯,接受私信许愿
数据结构初阶:栈和队列
文章目录
栈和队列
栈和队列是两种数据结构,栈和队列这两种结构也是线性表。特殊在于它们的操作受到一些限制。
1 栈
1.1 栈的定义和结构
栈是一种特殊的线性表,栈只允许在其固定的一端进行插入和删除元素的操作。进行数据插入删除操作的一端被称为栈顶,另一端被称为栈底。栈中的数据元素遵循后进先出的原则。
后进先出,先进后出,即
LIFO原则(Last In First Out)。
压栈:栈的插入操作被称为压栈,也可以叫做进栈、入栈。
出栈:栈的插入操作被称为出栈,或称弹栈。

数据的出入都在栈顶,类似于子弹上膛和发射的过程。元素像子弹一样一个个地被压入弹夹,再一个个地打出去,这个过程便是压栈和出栈,弹夹便是栈。
栈结构体定义
和线性表类似,栈结构可以使用数组栈和链式栈实现。相对来说,数组栈比链式栈的结构优势更大一点。
动态数组进行尾插尾删的效率高其次缓存命中率高,缺点是动态增容有一定的内存消耗。链式栈需使用双向链表,否则进行尾删的效率低,但以链表头作栈顶进行头插头删的效率要更高。
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
a指向为栈开辟的空间,top指向栈顶,相当于顺序表的size。
1.2 栈的实现
//初始化栈
void StackInit(ST* ps);
//入栈
void StackPush(ST* ps, STDataType data);
//出栈
void StackPop(ST* ps);
//获取栈顶元素
STDataType StackTop(ST* ps);
//获取栈元素个数
int StackSize(ST* ps);
//检测空栈
bool StackEmpty(ST* ps);
//销毁栈
void StackDestroy(ST* ps);
栈初始化和销毁
void StackInit(ST* ps) {
ps->a = NULL;
ps->capacity = ps->top = 0;
}
void StackDestroy(ST* ps) {
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = ps->top = 0;
}
top可以初始化为0,也可以为-1。
- 若为0,则
top总是即将插入元素的下标,或者说是栈顶的后一块空间,其值代表栈元素个。 - 若置为-1,则代表当前栈顶位置下标,其值加1代表元素个数。
栈的压入和弹出
void StackPush(ST* ps, STDataType data) {
assert(ps);
//检测容量
if (ps->capacity == ps->top) {
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* ptr = realloc(ps->a, sizeof(STDataType) * newCapacity);
if (ptr == NULL) {
perror("StackPush::realloc");
exit(-1);
}
ps->a = ptr;
ps->capacity = newCapacity;
}
ps->a[ps->top] = data;
ps->top++;
}
void StackPop(ST* ps) {
assert(ps);
assert(!StackEmpty(ps));
ps->top--;
}
入栈一定记得最后把
newCapacity再赋值给capacity,还有扩容时的大小应是数组元素的大小而不是结构体的大小。
删除数据前需要保证栈的非空状态。
获取栈顶元素
STDataType StackTop(ST* ps) {
assert(ps);
assert(!StackEmpty(ps));
return ps->a[ps->top - 1];
}
void test() {
while (!StackEmpty(&stack)) {
printf("%d ", StackTop(&stack));
StackPop(&stack);
}
}
top-1为当前栈顶的下标。同样要保证栈非空。
加上该测试函数,可以实现循环打印栈元素的功能。
其他基本接口
//获取栈元素个数
int StackSize(ST* ps) {
assert(ps);
return ps->top;
}
//检测空栈
bool StackEmpty(ST* ps) {
assert(ps);
return !ps->top;
}
!top的值正好可以表示栈的有无元素的状态。当然这样top必须初始化为0。
2 队列
2.1 队列的定义和结构
队列同样是一种特殊的线性表,和栈相反,队列只允许在其一端进行插入而在另一端进行删除元素的操作。进行数据插入操作的一端被称为队尾,进行删除操作的另一端被称为队头。队列中的数据元素遵循先进先出的原则。
入队列即在队尾插入数据,出队列则是在队头删除数据。
先进先出,后进后出,即
FIFO原则(First In First Out)。

队列结构体定义
typedef int QDataType;
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
} QueueNode;
typedef struct Queue
{
struct QueueNode* head;
struct QueueNode* tail;
} Queue;
队列需要两个指针标识队头和队尾,以便管理队列的元素。而队列元素即结点用单链表的结构实现即可。把结点封装成一个结构体,队列再封装成一个结构体存入指向结点结构体的指针。
队尾指针是根据队列这个对象只在队尾进行插入操作的特点而设计的。原先的单链表表尾有插入删除两种操作,故定义尾指针的意义不大,将存储的功能交给双向链表完成。
结构的定义是很灵活的,不定义
Queue结构体或者说不将头尾指针封装起来也是可以的。那么函数就需要定义成:void QueueInit(QueueNode** pphead, QueueNode** pptail);显然,封装成结构体不失为一种良好的代码风格。
2.2 队列的实现
//队列初始化
void QueueInit(Queue* pq);
//队列销毁
void QueueDestroy(Queue* pq);
//队列入队
void QueuePush(Queue* pq, QDataType x);
//队列出队
void QueuePop(Queue* pq);
//获取队头数据
QDataType QueueFront(Queue* pq);
//获取队尾数据
QDataType QueueBack(Queue* pq);
//获取队列元素个数
int QueueSize(Queue* pq);
//检测队列是否为空
bool QueueEmpty(Queue* pq);
队列初始化和销毁
void QueueInit(Queue* pq) {
assert(pq);
pq->head = NULL;
pq->tail = NULL;
}
void QueueDestroy(Queue* pq) {
assert(pq);
QueueNode* cur = pq->head;
while (cur) {
QueueNode* next = cur->next;
free(cur);
cur = next;
}
}
初始化和销毁并没有传二级指针,因为传递结构体的地址,而两个指针是封装在结构体里的。创建队列在函数外,所以传其地址就行,同时加上断言以防空指针。
队尾入队和队头出队
void QueuePush(Queue* pq, QDataType x) {//Enqueue
assert(pq);
QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
if (newNode == NULL) {
perror("Queue::malloc");
exit(-1);
}
newNode->data = x;
newNode->next = NULL;
//队列为空
if (pq->head == NULL) {
pq->head = pq->tail = newNode;
}
else {
pq->tail->next = newNode;
pq->tail = newNode;
}
}
void QueuePop(Queue* pq) {//Dequeue
assert(pq);
assert(!QueueEmpty(pq));
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
//链表为空时尾指针置空
if (pq->head == NULL) {
pq->tail = NULL;
}
}
在tail所指的队尾后再新建并链上一个结点,再将tail指针指向新结点,这便是入队的原理。出队只能在队头删除结点,也就是将head指针指向下一个结点并将前一个释放掉即可。
head->next对头指针解引用,就一定要保证head有next,也就是保证链表非空。

获取队头队尾元素
QDataType QueueFront(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
QDataType QueueBack(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
与出栈的实现类似,获取队列元素tail->data,对指针解引用访问其所指空间,必然要检查指针是否有效,也就是判断链表是否为空。
void test() {
//...
while (!QueueEmpty(&q)) {
printf("%d ", QueueFront(&q));
QueuePop(&q);
}
}
配合上述函数可以模拟实现循环出队。
其他基本接口
//获取队列元素个数
int QueueSize(Queue* pq) {
assert(pq);
int count = 0;
QueueNode* cur = pq->head;
while (cur) {
count++;
cur = cur->next;
}
return count;
}
//检测队列是否为空
bool QueueEmpty(Queue* pq) {
assert(pq);
return !pq->head;
}
获取队列元素个数,除了遍历计数的方式,还可以定义一个整型变量放在结点结构体中。
3 栈和队列面试题
Example 1 判断有效括号
给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。
bool isValid(char* s) {
ST st;
StackInit(&st);
while (*s) {
if (*s == '(' || *s == '[' || *s == '{') {
StackPush(&st, *s);
}
else {
//栈无元素,无法与右括号匹配
if (StackEmpty(&st)) {
StackDestroy(&st);
return false;
}
STDataType ret = StackTop(&st);
if ((ret == '(' && *s != ')') || (ret == '[' && *s != ']') || (ret == '{' && *s != '}')) {
StackDestroy(&st);
return false;
}
else {
StackPop(&st);
}
}
s++;
}
if (StackEmpty(&st)) {
StackDestroy(&st);
return true;
}
else {
StackDestroy(&st);
return false;
}
}
利用栈的先进后出,后进先出的特点。
- 将字符串
s从前向后遍历将其中所有左括号依次入栈, - 等待遇到右括号时再利用后进先出的特点就可将最近的左括号与右括号对比。
- 若匹配成功则出栈一次,下一次就可以找到前一个左括号与之后的右括号进行匹配。

Example 2 队列实现栈
使用两个队列实现一个后入先出的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)
如用数组用链表实现,换成用队列实现栈。即利用队列的结构和接口函数,也就是队列的特点实现出一个结构,该结构具有栈的特点。
/**
* 结构体定义
**/
typedef struct QueueNode {
QDataType data;
struct QueueNode* next;
}QueueNode;
typedef struct Queue {
struct QueueNode* head;
struct QueueNode* tail;
}Queue;
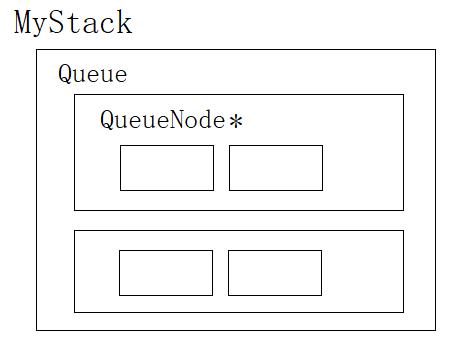
typedef struct {
Queue q1;
Queue q2;
} MyStack;
/**
* 接口函数定义
**/
MyStack* myStackCreate() {
MyStack* st = (MyStack*)malloc(sizeof(MyStack));
if (st == NULL) {
exit(-1);
}
QueueInit(&st->q1);
QueueInit(&st->q2);
return st;
}
//调用函数创建堆区结构体并返回
void myStackPush(MyStack* obj, int x) {
assert(obj);
//向非空队列Push
if (!QueueEmpty(&obj->q1)) {
QueuePush(&obj->q1, x);
}
else {
QueuePush(&obj->q2, x);
}
}
int myStackPop(MyStack* obj) {
assert(obj);
//定义空与非空队列
Queue* emptyQ = &obj->q1;
Queue* nonEmptyQ = &obj->q2;
if (!QueueEmpty(&obj->q1)) {
nonEmptyQ = &obj->q1;
emptyQ = &obj->q2;
}
//将非空队列前n-1个元素Push到空队列
while (QueueSize(nonEmptyQ) > 1) {
QueuePush(emptyQ, QueueFront(nonEmptyQ));
QueuePop(nonEmptyQ);
}
//Pop最后一个元素并返回
int top = QueueFront(nonEmptyQ);
QueuePop(nonEmptyQ);
return top;
}
int myStackTop(MyStack* obj) {
assert(obj);
//返回非空队列队尾元素
if (!QueueEmpty(&obj->q1)) {
return QueueBack(&obj->q1);
}
else {
return QueueBack(&obj->q2);
}
}
bool myStackEmpty(MyStack* obj) {
assert(obj);
//二者皆空才为空
return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj) {
assert(obj);
//释放队列结点
QueueDestroy(&obj->q1);
QueueDestroy(&obj->q2);
//释放结构体
free(obj);
}
Push,由于栈和队列都是从固定的一端入,故模拟入栈直接向非空队列入即可。
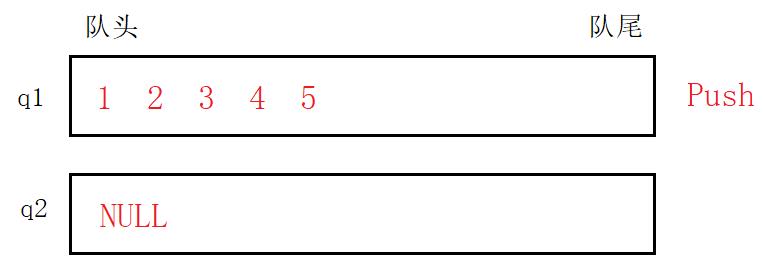
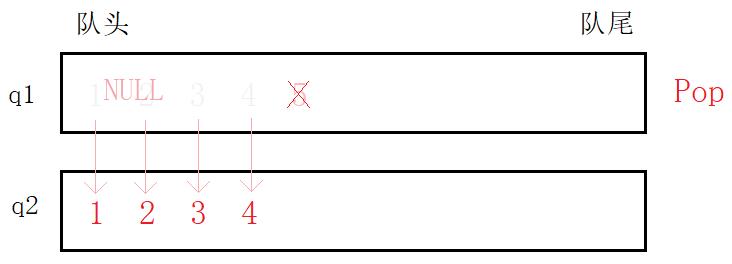
Pop,模拟出栈时,就要考虑到二者的不同,先删除队列中的前 n − 1 n-1 n−1个元素并将其入到另一个空队列中。直至第 n n n个元素再将其删除。
队头出数据,队尾入数据,正好能将非空队列前 n n n个元素按照原顺序插入到空队列中。非空队列仅剩最后一个元素再删除掉。将所插队列视为出栈后的栈,便实现模拟出栈的过程。
Top,直接调用队列读取队尾元素的接口函数即可。
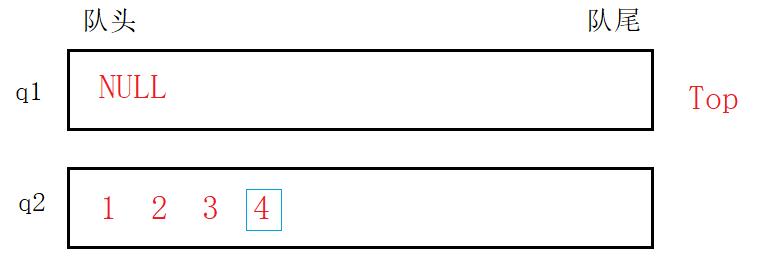
完成任意操作后都会产生一个空队列和一个非空队列。通过加以判断可以将非空队列视为待操作对象。也就是每次操作都是操作非空队列。
Example 3 栈实现队列
使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
/**
* 结构体定义
**/
typedef int STDataType;
typedef struct Stack {
STDataType* a;
int top;
int capacity;
}ST;
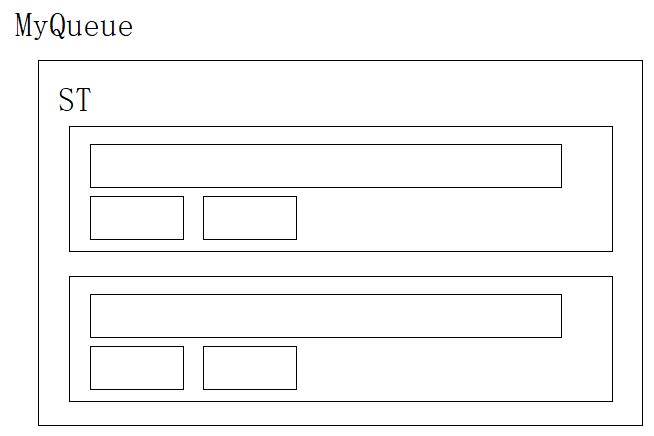
typedef struct {
ST pushST;
ST popST;
} MyQueue;
/**
* 接口函数定义
**/
MyQueue* myQueueCreate() {
MyQueue* pq= (MyQueue*)malloc(sizeof(MyQueue));
if (pq == NULL) {
exit(-1