无所畏惧的求和题解
本题是本人目前出的题中难度最高的题。
可能可以评一个黑?可能有点过,但是紫色是肯定可以的。
题目链接:无所畏惧的求和 - 洛谷
尽情享受吧!
这道题其实做法有很多:
那么这里讲解前两种方式
代数公式
自然数幂方求和公式?在高等教育出版社出版的《数学手册》中有这么一些公式:
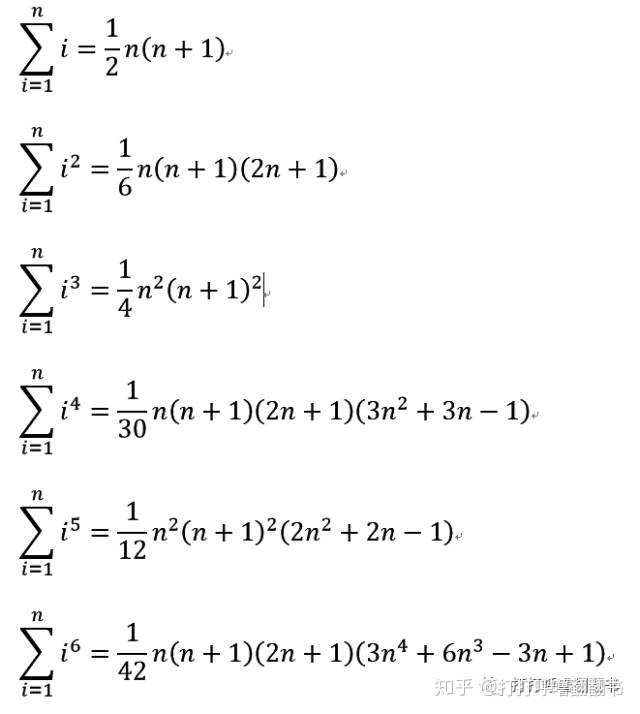
采用万能的数学归纳法可以一一证明上述公式。此处不提。
但是观察上述公式,可以发现一个特征:自然数 \\(k\\) 次幂求和公式是关于 \\(n\\) 的 \\(k + 1\\) 次有理多项式。
也就是
\\[\\sum_i=1^n i^k = \\sum_j=1^k+1 a_j n^j
\\]
知道上述结果之后,可采用待定系数法,也就是写出 \\(n = 1, 2, 3, \\dots, k+1\\) 的 \\(k + 1\\) 个代数式,利用矩阵求解即可。
举个例子,对于 \\(k = 3\\) 的情况:
\\[\\beginaligned
\\sum_i=1^1 i^3 &= a_1 + a_2 + a_3 + a_4 &= 1 \\\\
\\sum_i=1^2 i^3 &= 2a_1 + 4a_2 + 8a_3 + 16a_4 &= 9 \\\\
\\sum_i=1^3 i^3 &= 3a_1 + 9a_2 + 27a_3 + 81a_4 &= 36 \\\\
\\sum_i=1^4 i^3 &= 4a_1 + 16a_2 + 64a_3 + 256a_4 &= 81 \\\\
\\endaligned
\\]
那么借此求出每一项的系数即可对于每一个询问在 \\(O(k)\\) 的复杂度内完成计算。
总的复杂度为 \\(O(k^3 + T \\cdot k)\\)。但是,很明显,对于每一个测试点不会有所有的 \\(k\\)。所以请在必要时再计算系数。
组合公式
这个方法相对优秀一点点。标程就是用的此写法。
其实不难发现,对于 \\(x^k\\),我们可以改写为:
\\[x^k = \\sum_i=1^k a_i\\binomki
\\]
那么依据某些公式推导:
\\[\\sum_x=1^n x^k = \\sum_i = 2^k + 1 a_i-1 \\binom n+1i
\\]
所以,类似的,我们也可以枚举 \\(n = 1, 2, 3, \\dots, k\\) 来寻找其系数:
以 \\(k = 3\\) 为例
\\[\\beginaligned
\\sum_x=1^1 &= a_1 \\binom 22 + a_2 \\binom 23 + a_3 \\binom 24 = 1 \\\\
\\sum_x=1^2 &= a_1 \\binom 32 + a_2 \\binom 33 + a_3 \\binom 34 = 9 \\\\
\\sum_x=1^3 &= a_1 \\binom 42 + a_2 \\binom 43 + a_3 \\binom 44 = 36 \\\\
\\endaligned
\\]
同时我们规定 \\(\\binom nr = 0\\ (n \\lt r)\\)。所以上式也可以写为
\\[\\beginaligned
\\sum_x=1^1 &= a_1 \\binom 22 &= 1 \\\\
\\sum_x=1^2 &= a_1 \\binom 32 + a_2 \\binom 33 &= 9 \\\\
\\sum_x=1^3 &= a_1 \\binom 42 + a_2 \\binom 43 + a_3 \\binom 44 &= 36 \\\\
\\endaligned
\\]
这就是一个下三角矩阵,每一次扫一遍即可。
代码也非常简单,常数比第一种方法小很多:
void get_coefficient(int k, int * ccts)
int sum = 0;
for (int n = 1; n <= k; ++n)
sum += qpow(n, k, MOD);
int rest = sum;
// 由于我们已经知道了前 (n-1) 个系数,直接通过总和一一减去即可。
for (int i = 1; i < n; ++i)
// 注意 k < MOD,所以此处不需要Lucas
(rest -= ccts[i] * C(n + 1, i + 1) % MOD) %= MOD;
if (rest < 0) rest += MOD;
// 明显可知,C(n, n) = 1,所以剩下的即是系数
ccts[n] = rest;
核心部分也非常简单,只是模数较小,需要用到 \\(Lucas\\) 定理。
int ccts[K][K]; // 用于保存系数
void work()
int T, n, k;
cin >> T;
while (T--)
cin >> n >> k;
int * cctk = ccts[k];
if (!cctk[1]) // 其实不难发现,a1 一定为 1,所以借此判断即可
get_coefficient(k, cctk);
int ans = 0;
for (int i = 1; i <= k; ++i)
(ans += cctk[i] * Lucas(n + 1, i + 1)) %= MOD;
cout << ans << \'\\n\';
大家都说这题水然而我好像还是调了有一会儿……不过暴力真的很良心,裸的暴力竟然还有60分。
打一张表出来,就会发现数据好像哪里有规律的样子,再仔细看一看,就会发现k/3~k/2为公差为2的等差数列,k/2~之后为公差为1的等差数列,于是我们就可以利用高斯求和快速求解啦。自认为代码是能够看得的...
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define int long long
LL ans;
int p, x = 10, n, m, k, base, skipper;
LL Get_sum()//高斯求和,从p项开始公差为x
{
int y = x - 1;
int base = (k % p);
int end = max(base % y, base - (m - p) * y);
skipper = ((base - end) / y) + 1;
return ((LL)(base + end) * (LL)skipper) >> 1;
}
void init()//分段设x值
{
if(k > 1000000) x = 1555;
else if(k > 5000000) x = 600;
else if(k > 300000) x = 100;
else if(k > 5000) x = 50;
else x = 2;
}
signed main()
{
scanf("%lld%lld", &n, &k);
m = min(n, k);
init();
for(p = 1; p <= m; p ++)
{
if(p == (k / x) + 1)
{
ans += Get_sum();
p += (skipper - 1);//统计加了多少项
x -= 1;
}
else ans += (k % p);
}
if(n > k) ans += (LL) (n - k) * (LL) (k);
printf("%lld", ans);
return 0;
}