01关于满减优惠券可叠加使用场景下的动态规划算法

Posted 2023-03-31 huageyiyangdewo

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了01关于满减优惠券可叠加使用场景下的动态规划算法相关的知识，希望对你有一定的参考价值。

01、关于满减优惠券可叠加使用场景下的动态规划算法

之前在一家公司做停车业务，做优惠券相关的内容。有一期需求是关于满减优惠券可叠加使用场景下，为用户推荐最优的优惠券使用方案，特意在网上找了些资料学习，这里做个记录，方便学习。

后面在网上找到了类似的需求，放在了文章的最后，特别感谢原作者。

1、需求简介

需求描述为：支付停车费时，有多张满减优惠券可用（可叠加使用），求最优策略（减免最多）。

准确描述为：

设共有n张优惠券C: [(V1, D1), (V2, D2), (V3, D3), ..., (Vn, Dn)]，其中Vn为面值，Dn为减免值（对于一张优惠券Cx，满Vx减Dx），优惠券为单张，可叠加使用（使用过一张后，如果满足面值还可以使用其他优惠券）。

求停车费用为M时，使用优惠券的最优策略：1.减免值最多，2.优惠券剩余最优（比如对于 C1 (2, 0.1) 、C2 (1, 0.1) 只能选择一张的最优取舍就是用C1留C2 ）。

示例：

输入：

C = [(2, 1.9), (1, 1), (1, 0.1), (2, 0.1)] , M = 3

期望输出：

使用优惠券：[(2, 0.1), (2,1.9), (1,1)]

总减免：3

满减优惠券可叠加使用的场景下的解决方案，可背包算法相似，通过动态算法规划算法背包问题学习了下背包的思想。顺便了解一下动态规划能解决什么问题：

适用动态规划方法求解的最优化问题应该具备的两个要素：最优子结构和子问题重叠。——《算法导论》动态规划原理

优惠券问题看起来和背包问题很像，但是有一点不同。

2、优惠券问题和背包问题的不同点

图中，背包问题里面的数据为：在负重已知的前提下能装物品的最优总价值；优惠券问题里面的数据为总金额能使用优惠券的最优总减免值。

对于背包问题，如果负重为4，策略只能是拿B号物品，因为拿取B号之后负重还剩（4-3=1），再拿不了A号物品了（最终价值为1.5）；

对于优惠券问题，如果金额为4，使用完B号优惠券之后，金额还剩（4-1.5=2.5），还可以再用A号优惠券的（最终减免值为2.5）。

总结这个不同就是：

背包判断大于重量W，再减去W，得到剩余值，根据剩余值再去上一层找剩余值对应的值（统计价值），背包问题是减去重量W；
优惠券则是当总金额M大于面额V时，再减去减免值D，得到剩余的金额N，再根据金额N去上一层找对应的值（统计减免值D），优惠券问题是减去减免值D。

而且因为这个不同，优惠券问题的数据对优惠券顺序是有要求的，不像背包问题中，总是负重减物品重量，剩余的重量直接去找上次最优再计算就好了。顺序问题分两种：

3、优惠券的顺序问题

3.1 对于优惠券，不同面额的顺序

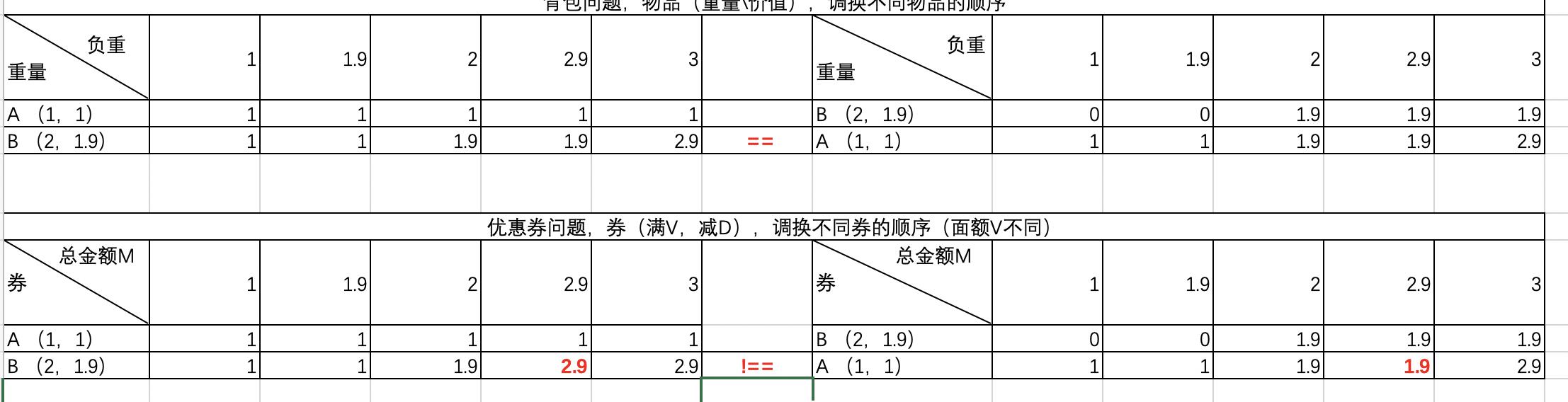
优惠券面额顺序对结果的影响

图中，将物品和券的顺序颠倒，对于背包问题，最后一行数据完全相同，对结果无影响；

对于优惠券问题，顺序变了结果会不一样。（因为需要满足优惠券(v,d), 中的v才能减去第二项，所以对顺序有要求）。

所以，不同面额 (V不同) 的优惠券，应该升序排列。

3.2 面额相同，减免值不同

优惠券面额相同，不同减免值的顺序对结果的影响

因为背包思想是通过上一次的结果来铺垫下一次的值，所以从上往下需要先生成同额度的最优值。

所以，同面额不同减免值 (V同D不同) 的优惠券，应该降序排列。

排序示例为：

[
    (2, 1.9), 
    (1, 1), 
    (1, 0.1), 
    (2, 0.1)
]

需排列为:

[
    (1, 1),
    (1, 0.1),
    (2, 1.9),
    (2, 0.1),
]

综以上 一点不同两种顺序 的情况所述，使用背包之前需要排序（V升D降），按V升序，如果V相同，再按D降序排。再使用背包算法（大于V减去D）。

对于上面的排序要求，我们知道，需要使用具有稳定性的排序算法，下面使用归并排序来进行计算。注意：排序算法一定要具有稳定性，否则无效。

4、程序实现

4.1 具有稳定性的排序算法

def merge(nums: list[int], left: int, mid: int, right: int) -> None:
    """ 合并左子数组和右子数组 """
    # 左子数组区间 [left, mid]
    # 右子数组区间 [mid + 1, right]
    # 初始化辅助数组
    tmp: list[int] = list(nums[left:right + 1])
    # 左子数组的起始索引和结束索引
    left_start: int = 0
    left_end: int = mid - left
    # 右子数组的起始索引和结束索引
    right_start: int = mid + 1 - left
    right_end: int = right - left
    # i, j 分别指向左子数组、右子数组的首元素
    i: int = left_start
    j: int = right_start
    # 通过覆盖原数组 nums 来合并左子数组和右子数组
    for k in range(left, right + 1):
        # 若“左子数组已全部合并完”，则选取右子数组元素，并且 j++
        if i > left_end:
            nums[k] = tmp[j]
            j += 1
        # 否则，若“右子数组已全部合并完”或“左子数组元素 <= 右子数组元素”，则选取左子数组元素，并且 i++
        elif j > right_end or tmp[i] <= tmp[j]:
            nums[k] = tmp[i]
            i += 1
        # 否则，若“左右子数组都未全部合并完”且“左子数组元素 > 右子数组元素”，则选取右子数组元素，并且 j++
        else:
            nums[k] = tmp[j]
            j += 1

def merge_sort(nums: list[int], left: int, right: int) -> None:
    """ 归并排序 """
    # 终止条件
    if left >= right:
        return                        # 当子数组长度为 1 时终止递归
    # 划分阶段
    mid: int = (left + right) // 2    # 计算中点
    merge_sort(nums, left, mid)       # 递归左子数组
    merge_sort(nums, mid + 1, right)  # 递归右子数组
    # 合并阶段
    merge(nums, left, mid, right)


""" Driver Code """
if __name__ == \'__main__\':
    nums: list[int] = [ 7, 3, 2, 6, 0, 1, 5, 4 ]
    merge_sort(nums, 0, len(nums) - 1)
    print("归并排序完成后 nums =", nums)

4.2 优惠券叠加算法

# coding:utf-8
# 背包算法，解决满减优惠券叠加使用问题

def coupon_bags(coupon, amount):
    """
        优惠券背包算法
        param: coupon 优惠券数组
        param: amount 金额
    """
    # 转换金额跨度（间隔）： 元->角
    span = 10
    amount = int(amount*span)

    for i, v in enumerate(coupon):
        for j in range(len(v)):
            coupon[i][j] = int(coupon[i][j]*span)

    # 初始化结果数组，dps 存储满减值（背包算法结果）
    # dps_coupons 存储 dps 对应满减值下使用的 优惠券方案
    dps = []
    dps_coupons = []
    # len(coupon)+1，这里为什么要加 1，
    # 记住 动态算法规划算法背包问题一文中的： dp[i][0] = dq[0][j]=0;原因就是这个
    for i in range(len(coupon)+1):
        # 这里为啥是 amount+1,因为 dps 中的索引是从0开始的，
        # 索引0的位置处存的是金额0的满减值，所以这里需要 amount+1
        dps.append(list((0,)*(amount+1)))

        # list 直接 * 生成的是同一list，用循环生成
        dps_coupons.append([])
        for j in range(amount+1):
            dps_coupons[i].append([])

    for i in range(1, len(coupon)+1):
        # i 代表第 i 张优惠券，从 1 开始的
        for j in range(1, amount+1):
            # j 代表的是 总金额M为：j
            # coupon[i-1][0] 代表的是优惠券的中的 V，即满 coupon[i-1][0] 减 coupon[i-1][1]
            if j < coupon[i-1][0]:  # 金额j 达不到 满减的条件：V，取上一层对应位置的值
                # 获取上个策略值
                dps[i][j] = dps[i-1][j]
                dps_coupons[i][j] = dps_coupons[i-1][j]
            else:  # 金额j 达到了 满减的条件：V

                # dps中的i代表的是第几张优惠券，j代表的是总金额为J时的最优满减值
                # coupon[i - 1][1]，代表的是：当前优惠券的减免值
                # dps[i - 1][j - coupon[i - 1][1]]，代表的是剩余金额对应的最优满减值
                if dps[i - 1][j] > coupon[i - 1][1] + dps[i - 1][j - coupon[i - 1][1]]:
                    # 上一行同列数据 优于 当前优惠券+剩余的金额对应的上次数据，取之前数据
                    dps[i][j] = dps[i-1][j]
                    dps_coupons[i][j] = dps_coupons[i-1][j]
                else:
                    # 选取当前+剩余 优于 上一行数据
                    dps[i][j] = dps[i-1][j-coupon[i-1][1]]+coupon[i-1][1]
                    # dps_coupons[i-1][j-coupon[i-1][1]]，值是list，需要拷贝，才不会影响之前的结果
                    dps_coupons[i][j] = dps_coupons[i-1][j-coupon[i-1][1]].copy()
                    # 表示使用了第 i 张优惠券
                    dps_coupons[i][j].insert(0, list(coupon[i-1]))

    # 结果需返回数据原单位（元）
    result_coupons = dps_coupons[-1][-1].copy()
    for i, v in enumerate(result_coupons):
        for j in range(len(v)):
            result_coupons[i][j] = result_coupons[i][j]/span
    print(f"使用优惠券：result_coupons 总减免：dps[-1][-1]/span")


# 优惠券
coupon_items = [
    [1, 1],
    [1, 0.1],
    [2, 1.9],
    [2, 0.1],
]
# 举例中的优惠券是最终顺序。确保优惠券已经排序过，多维升序(V升D降)，此处省略
coupon_bags(coupon_items, 3)
"""
coupon_items = [
    [1, 0.6],
    [2, 0.7],
    [2, 1.3],
    [3, 2.3],
]
coupon_bags(coupon_items, 5)
"""

dps,dps_coupons数据存储示意图

4.3 停车场优惠券叠加使用的场景

上面就是将上面两种算法结合在一起进行使用。

class CouponSort(object):
    """
    具有稳定性的归并排序
    coupon_list: [[5, 1, 189], [6, 1, 200]]
    [5, 1, 189] --> 5: 总金额为5，1：减免值，189：此张优惠券对应数据库中的记录ID
    """
    def __init__(self, coupon_list):
        tmp = coupon_list.copy()
        self.coupon_list = tmp
        self.length = len(coupon_list)

    def sort(self):
        left = 0
        right = self.length
        self._merge_sort(left, right - 1, True)

        # 下面是当总金额M相同时，按照减免值降序排序
        start, end, index = 0, 0, 0
        while index != self.length:
            if index != self.length - 1:
                if self.coupon_list[index][0] != self.coupon_list[index + 1][0]:
                    self._merge_sort(start, end, False)
                    start = index + 1
                    end = start
                else:
                    end += 1
            else:
                self._merge_sort(start, end, False)
            index += 1

        return self.coupon_list

    def _merge_sort(self, left, right, l2m):
        """ 归并排序 """
        # 终止条件
        if left >= right:
            return  # 当子数组长度为 1 时终止递归
        # 划分阶段
        mid = (left + right) // 2  # 计算中点
        self._merge_sort(left, mid, l2m)  # 递归左子数组
        self._merge_sort(mid + 1, right, l2m)  # 递归右子数组
        # 合并阶段
        self._merge(left, mid, right, l2m)

    def _merge(self, left, mid, right, l2m):
        """ 合并左子数组和右子数组 """
        # 左子数组区间 [left, mid]
        # 右子数组区间 [mid + 1, right]
        # 初始化辅助数组
        tmp = list(self.coupon_list[left:right + 1])
        # 左子数组的起始索引和结束索引
        left_start = 0
        left_end = mid - left
        # 右子数组的起始索引和结束索引
        right_start = mid + 1 - left
        right_end = right - left
        # i, j 分别指向左子数组、右子数组的首元素
        i = left_start
        j = right_start
        # 通过覆盖原数组 nums 来合并左子数组和右子数组
        for k in range(left, right + 1):
            if l2m:
                i, j = self._little2max(i, j, k, left_end, right_end, tmp)

            else:
                i, j = self._max2little(i, j, k, left_end, right_end, tmp)

    def _little2max(self, i, j, k, left_end, right_end, tmp):
        # 若“左子数组已全部合并完”，则选取右子数组元素，并且 j++
        if i > left_end:
            self.coupon_list[k] = tmp[j]
            j += 1
        # 否则，若“右子数组已全部合并完”或“左子数组元素 <= 右子数组元素”，则选取左子数组元素，并且 i++
        elif j > right_end or tmp[i][0] <= tmp[j][0]:
            self.coupon_list[k] = tmp[i]
            i += 1
        # 否则，若“左右子数组都未全部合并完”且“左子数组元素 > 右子数组元素”，则选取右子数组元素，并且 j++
        else:
            self.coupon_list[k] = tmp[j]
            j += 1
        return i, j

    def _max2little(self, i, j, k, left_end, right_end, tmp):
        # 若“左子数组已全部合并完”，则选取右子数组元素，并且 j++
        if i > left_end:
            self.coupon_list[k] = tmp[j]
            j += 1
        # 否则，若“右子数组已全部合并完”或“左子数组元素 <= 右子数组元素”，则选取左子数组元素，并且 i++
        elif j > right_end or tmp[i][1] >= tmp[j][1]:
            self.coupon_list[k] = tmp[i]
            i += 1
        # 否则，若“左右子数组都未全部合并完”且“左子数组元素 > 右子数组元素”，则选取右子数组元素，并且 j++
        else:
            self.coupon_list[k] = tmp[j]
            j += 1
        return i, j


def _coupon_bags(coupon, amount):
    """
        优惠券背包算法
        param: coupon 优惠券数组
        param: amount 金额
    """
    # 转换金额跨度（间隔）： 元->角
    span = 10
    amount = int(amount*span)

    for i, v in enumerate(coupon):
        for j in range(len(v)):
            coupon[i][j] = int(coupon[i][j]*span)

    # 初始化结果数组，dps 存储满减值（背包算法结果）
    # dps_coupons 存储 dps 对应满减值下使用的 优惠券方案
    dps = []
    dps_coupons = []
    # len(coupon)+1，这里为什么要加 1，
    # 记住 动态算法规划算法背包问题一文中的： dp[i][0] = dq[0][j]=0;原因就是这个
    for i in range(len(coupon)+1):
        # 这里为啥是 amount+1,因为 dps 中的索引是从0开始的，
        # 索引0的位置处存的是金额0的满减值，所以这里需要 amount+1
        dps.append(list((0,)*(amount+1)))

        # list 直接 * 生成的是同一list，用循环生成
        dps_coupons.append([])
        for j in range(amount+1):
            dps_coupons[i].append([])

    for i in range(1, len(coupon)+1):
        # i 代表第 i 张优惠券，从 1 开始的
        for j in range(1, amount+1):
            # j 代表的是 总金额M为：j
            # coupon[i-1][0] 代表的是优惠券的中的 V，即满 coupon[i-1][0] 减 coupon[i-1][1]
            if j < coupon[i-1][0]:  # 金额j 达不到 满减的条件：V，取上一层对应位置的值
                # 获取上个策略值
                dps[i][j] = dps[i-1][j]
                dps_coupons[i][j] = dps_coupons[i-1][j]
            else:  # 金额j 达到了 满减的条件：V

                # dps中的i代表的是第几张优惠券，j代表的是总金额为J时的最优满减值
                # coupon[i - 1][1]，代表的是：当前优惠券的减免值
                # dps[i - 1][j - coupon[i - 1][1]]，代表的是剩余金额对应的最优满减值
                if dps[i - 1][j] > coupon[i - 1][1] + dps[i - 1][j - coupon[i - 1][1]]:
                    # 上一行同列数据 优于 当前优惠券+剩余的金额对应的上次数据，取之前数据
                    dps[i][j] = dps[i-1][j]
                    dps_coupons[i][j] = dps_coupons[i-1][j]
                else:
                    # 选取当前+剩余 优于 上一行数据
                    dps[i][j] = dps[i-1][j-coupon[i-1][1]]+coupon[i-1][1]
                    # dps_coupons[i-1][j-coupon[i-1][1]]，值是list，需要拷贝，才不会影响之前的结果
                    dps_coupons[i][j] = dps_coupons[i-1][j-coupon[i-1][1]].copy()
                    # 表示使用了第 i 张优惠券
                    dps_coupons[i][j].insert(0, list(coupon[i-1]))

    # 结果需返回数据原单位（元）
    result_coupons = dps_coupons[-1][-1].copy()
    for i, v in enumerate(result_coupons):
        for j in range(len(v)):
            result_coupons[i][j] = result_coupons[i][j]/span
    print(f"使用优惠券：result_coupons 总减免：dps[-1][-1]/span")

    return result_coupons, dps[-1][-1]/span


def find_max_discount(coupon_list, amount):
    # 这里应该对 coupon_list 中的元素有要求，即 coupon_list[i][0] >= coupon_list[i][1]
    # 否则在计算 最优使用方案时会报错，即：dps[i - 1][j - coupon[i - 1][1]]，
    # 要求：j - coupon[i - 1][1] >= 0
    cs = CouponSort(coupon_list)
    sort_coupon = cs.sort()
    print(sort_coupon)

    return _coupon_bags(sort_coupon, amount)


t = [[10, 1, 12], [20, 10, 43], [20, 15, 12], [24, 14, 1], [5, 4, 4], [66, 40, 15]]

find_max_discount(t, 100)

4.4 可优化的点

1、使用一维数组存储结果值。

2、dps 间隔优化（如果优惠券有分，span为100，那数组就很大了）。

对于上面的优化点有机会再去思考

以上就是关于停车场优惠券可叠加使用的解决方案，特此记录下，文中有错误的地方，恳请指出，谢谢。特别感谢下面两位大佬！！！

参考资料：

关于满减优惠券叠加的背包算法

归并排序

以上是关于01关于满减优惠券可叠加使用场景下的动态规划算法的主要内容，如果未能解决你的问题，请参考以下文章

算法应对电商的各种满减活动

华为OD机试 - 网上商城优惠活动（JavaScript） | 机试题+算法思路+考点+代码解析 2023

阿里云年中618-如何在活动的基础上叠加优惠券？

前方高能：1024程序员节读书攻略来来来来啦！

阿里云年中618大礼包如何领取及使用方法！