2023-03-30 图的深度优先遍历的应用
Posted 空無一悟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2023-03-30 图的深度优先遍历的应用相关的知识,希望对你有一定的参考价值。
图的深度优先遍历的应用
常见的应用如下
- 求图的连通分量(1~2)
- 求两点间是否可达(3)
- 求两点间的一条路径(4)
- 检测图是否有环(9)
- 二分图检测(10~11)
- 寻找图中的桥和割点
- 哈密尔顿路径
- 拓扑排序
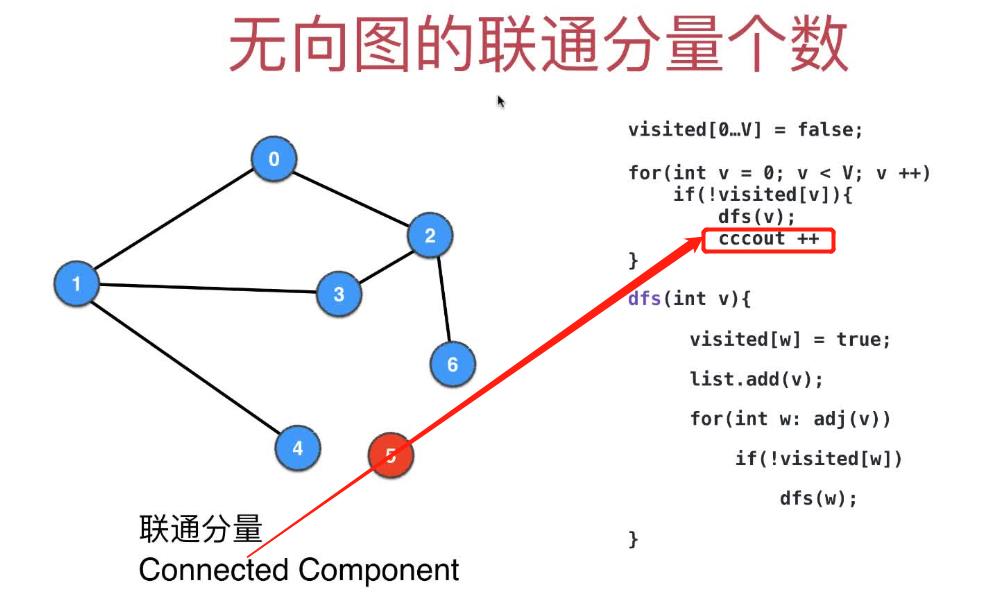
1 求无向图的连通分量的个数
DFS递归每退出一次,说明图有了一个连通分量,所以在dfs()下方,连通分量个数connectedComponentCount(
下图中的ccount)加1即可
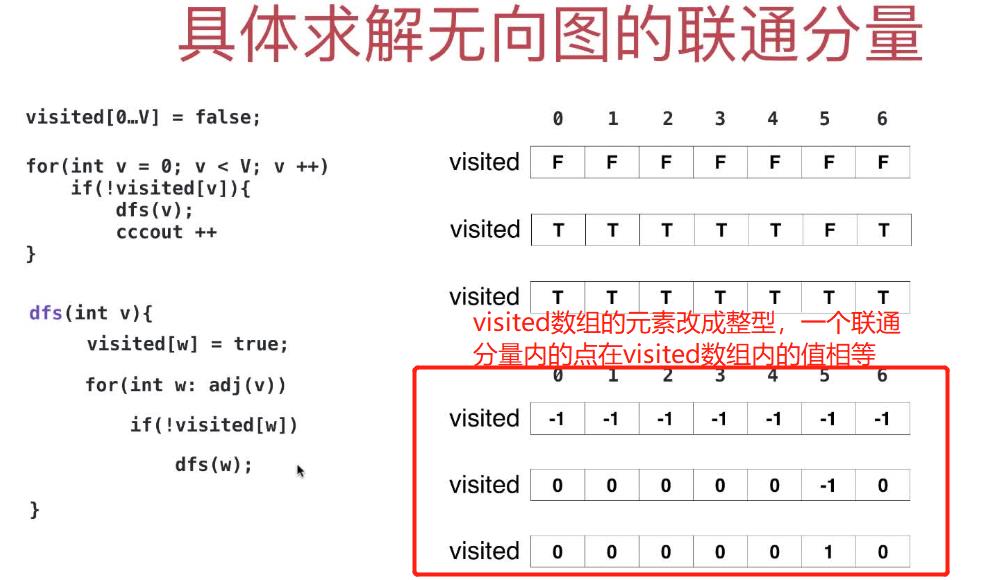
2 求每个连通分量里各自具体有哪些节点
实际就是改造visited[]数组,把boolean类型改成整型,
不同的连通分量标记为"已访问"时用不同的整数去记录(未被访问默认是-1,访问后用地是当前的联通分量的个数即connectedComponentCount的值),同一个联通分量内的顶点在visited[]中的值相等
在递归中把当前的联通分量个数传给dfs()作为联通分量的编号,即visited[当前点]的值
public GraphDFS4ConnectedComponentsStatistic(Graph graph)
this.graph = graph;
// 初始化访问数组,用图的顶点个数来访问
visited = new int[graph.V()];
// 数组初始化为-1
Arrays.fill(visited, -1);
// 从dfs(0)改成下面的代码,可以支持非连通的图
for (int v = 0; v < graph.V(); v++) // 等于-1表示还没被访问过
if (visited[v] == -1)
// 第二个参数表示当前连通分量的标志(多个连通分量内的元素在visited内用connectedComponentCount这个值进行标记)
dfs(v, connectedComponentCount);
// 当退出递归时,相当于结束了一个连通图的遍历,所以连通分量数加1
connectedComponentCount++;
然后在dfs函数中把当前点v用上面传入的connectedComponentCount设置为已访问
/**
* 深度优先遍历
*
* @param v 当前遍历到的顶点下标
* @param ccid 当前连通分量的标记(同一个连通分量内的元素都在visited数组内用这个数值进行赋值标记)
*/
private void dfs(int v, int ccid)
visited[v] = ccid;
orderList.add(v);
for (Integer w : graph.adj(v))
if (visited[w] == -1)
// w点没被访问的话就递归接着访问
dfs(w, ccid);
2020-4-22更新:使用List数组来记录每个联通分量更方便
public List<Integer>[] getCcDetail()
List<Integer>[] ccDetailArr = new ArrayList[ccCount];
// 一定注意要给数组内每个对象新建好List
for (int i = 0; i < ccDetailArr.length; i++)
ccDetailArr[i] = new ArrayList<>();
// ccCount即上面的connectedComponentCount
for (int ccid = 0; ccid < ccCount; ccid++)
for (int v = 0; v < visited.length; v++)
if (visited[v] == ccid)
ccDetailArr[ccid].add(v);
return ccDetailArr;
使用方法如下:
ccDetail = dfsccCount.getCcDetail();
for (int ccid = 0; ccid < ccDetail.length; ccid++)
System.out.println("联通分量" + ccid + "的顶点详情是:" + ccDetail[ccid]);
结果举例如下:
联通分量0的顶点详情是:[0, 1, 2, 3, 4, 6]
联通分量1的顶点详情是:[5]
3 判断两个点v和w在给定的图中是否是可连接connected地
只需要判断visited[v]是否和visited[w]相等即可,因为上一节已经实现了一个连通分量内的点其visited[i]的值是相等地了
/**
* 判断v和w在图中是否是可以连接地
*/
public boolean isConnected(int v, int w)
graph.validateVertex(v);
graph.validateVertex(w);
return visited[v] == visited[w];
ps:
以上是关于2023-03-30 图的深度优先遍历的应用的主要内容,如果未能解决你的问题,请参考以下文章