_排列与组合

Posted 2023-02-19 博客园/gengduc

第1章 排列与组合

1.1 排列与组合

定义：设A=\\(a_1\\),\\(a_2\\),\\(a_3\\),…\\(a_n\\)是\\(n\\)个不同元素的集合，\\(m\\)满足\\(0≤m≤n\\),任取A中个（不重复的）元素，按次序排列，称为从\\(n\\)个中取\\(m\\)个的（无重）排列，用\\(P_n^m\\)或\\(P(n,m)\\)表示。当\\(m=\\)n时，称为全排列。一般不说可重即无重。

\\[P(n,m)=n(n-1)···(n-m+1)=\\fracn!(n-m)! \\]

定义：当从\\(n\\)个元素中取出\\(m\\)个而不考虑它的顺序时，称为从\\(n\\)个中取\\(r\\)个的组合。用\\(C_n^m\\)或\\(C(n,m)\\)表示。

若在每一种组合的基础上，再将盒子标号区别，且对盒子进行排列，便得到\\(n\\)取\\(r\\)的排列，所以有\\(P(n,m)=C(n,m) \\cdot n!\\)

例题：试求由1,3,5,7组成的数字不重复出现的整数的总和？

解：这样的整数可以是1位数、2位数、3位数、4位数，其数目为\\(P_4^1+P_4^2+P_4^3+P_4^4=4+12+24+24=64\\)，即求这64个数的和。统计各自在个位、十位、百位、千位上数值的总和，设它们的总和分别为\\(S_1\\)、\\(S_2\\)、\\(S_3\\)、\\(S_4\\)，则问题所求的和\\(S=S_1+10S_2+100S_3+1000S_4\\)

（1）\\(S_1\\)的计算

一位数中个位数之和为\\((1+3+5+7)P_3^0=16\\)，

两位数中个位数之和为\\((1+3+5+7)P_3^1=48\\)（1在个位，十位有\\(P_3^1\\)种选择，3、5、7在个位同样如此）

三位数中个位数之和为\\((1+3+5+7)P_3^2=96\\)，

四位数中个位数之和为\\((1+3+5+7)P_3^3=96\\)，

故\\(S_1=(1+3+5+7)(P_3^0+P_3^1+P_3^2+P_3^3)=(16+48+96+96)=256\\)

（2）\\(S_2\\)的计算，即计算在十位数的和

\\(S_2=(1+3+5+7)(P_3^1+P_3^2+P_3^3)=16 \\times 15=240\\)

（3）\\(S_3\\)的计算

\\(S_3=(1+3+5+7)(P_3^2+P_3^3)=16 \\times 12=192\\)

（4）\\(S_4\\)的计算

\\(S_2=(1+3+5+7)P_3^3=16 \\times 6=96\\)

故\\(S=256+240 \\times 10+192 \\times 100 + 96 \\times 1000=117856\\)

1.2 加法法则与乘法法则

[加法法则] 设事件A有\\(m\\)种产生方式，事件B有\\(n\\)种产生方式，则事件A或B之一有\\(m+n\\)种产生方式。

[乘法法则] 设事件A有\\(m\\)种产生方式，事件B有\\(n\\)种产生方式，则事件A与B有\\(m \\cdot n\\)种产生方式。

1.3 一一对应

“一一对应”概念是一个在计数中极为基本的概念。一一对应既是单射又是满射。在组合计数时往往借助于一一对应实现模型转换。比如要对A集合计数，但直接计数有困难，于是可设法构造一易于计数的B，使得A与B一一对应。

例题：某保密装置须同时使用若干把不同的钥匙才能打开。现有7人，每人持若干把钥匙。须4人到场才能开锁。问：（1）至少有多少把不同的钥匙？（2）每人至少持几把钥匙？

解：由题知，要保证任意3个人到场都开不了锁，任意4个人到场才能开锁。

（1）任意3个人缺的钥匙都不同，如果甲乙丙缺的钥匙和甲乙丁缺的钥匙一样，那么他们4个人就不能开门了。也就是说，任意3个人都会缺一把钥匙，且他们缺的钥匙不一样。故至少有\\(C_7^3\\)种

（2）任意4个人都不缺钥匙，任意一人对于其他6人中的3人，都至少有一把不同的钥匙能配合着开门。即其他6人中的3人都缺一把钥匙，缺\\(C_6^3\\)把，需要第四个人至少有\\(C_6^3\\)把钥匙。故每人至少持\\(C_6^3\\)把钥匙。

1.4 多重排列

自由多重：\\(\\stackrel \\mathbfM=\\left\\\\infty a_1, \\infty a_2, \\cdots, \\infty a_n\\right\\\\)

受限多重：\\(\\mathbfM=\\left\\\\mathbfk_1 a_1, \\mathbfk_2 a_2, \\cdots, \\mathbfk_n a_n\\right\\\\)

在自由情况下，从\\(n\\)中取\\(m\\)个作多重排列，排列数\\(n^m\\)

在受限情况下，\\(k_1\\)个\\(a_1\\)，\\(k_2\\)个\\(a_2\\)，…，\\(k_m\\)个\\(a_m\\)的排列数，设\\(k_1+k_2+...+k_m=n\\)，设此排列数为\\(P(n;k_1,k_2,...,k_m)\\)

\\[P\\left(\\mathbfn; \\mathbfk_1, \\mathbfk_2, \\ldots, \\mathbfk_\\mathrmm\\right)=\\frac\\mathbfn !\\mathbfk_1 ! \\mathbfk_2 ! \\ldots \\mathbfk_\\mathrmm !=\\left(\\beginarrayc\\mathbfn \\\\ \\mathbfk_1 \\mathbfk_2 \\ldots \\mathbfk_m\\endarray\\right) \\]

这是一种元素重复的排列！

例题：用长度为\\(1\\times1\\),\\(1\\times2\\),\\(1 \\times 3\\)的方砖铺设\\(1 \\times 7\\)的模块，有几种方式？

解：（1）用7块\\(1 \\times 1\\)的砖，有\\(1\\)种方式。

（2）用5块\\(1 \\times 1\\)的砖，1块\\(1 \\times 2\\)的砖，有\\(\\frac6!5!=6\\)种方式

（3）用4块\\(1 \\times 1\\)的砖，1块\\(1 \\times 3\\)的砖，有\\(\\frac5!4!=5\\)种方式

（4）用3块\\(1 \\times 1\\)的砖，2块\\(1 \\times 2\\)的砖，有\\(\\frac5!3! \\cdot 2!=10\\)种方式

（5）用2块\\(1 \\times 1\\)的砖，1块\\(1 \\times 2\\)的砖，1块\\(1 \\times 3\\)的砖，有\\(\\frac 4! 2!=12\\)种方式

（6）用1块\\(1 \\times 1\\)的砖，3块\\(1 \\times 2\\)的砖，有\\(\\frac4!3!=4\\)种方式

（7）用1块\\(1 \\times 1\\)的砖，2块\\(1 \\times 3\\)的砖，有\\(\\frac3!2!=3\\)种方式

（8）用2块\\(1 \\times 2\\)的砖，1块\\(1 \\times 3\\)的砖，有\\(\\frac3!2!=3\\)种方式

总共有1+6+5+10+12+4+3+3=44种方式

延伸1：特定排列也会产生多重排列结果

例题：10男10女乘车出游，每车2男2女，几种方案？假设车辆无区别

解：（1）多队分组？\\(\\frac(10 !)^25 ! \\times 2^10\\)

（2）若有一对男女要求同车呢？\\(\\frac(9 !)^24 ! \\times 2^8\\)

（3）若有两队男女要求同车呢？这要求同车的两队男女可以在一辆车上，也可以在两辆车上。如果在一辆车上，那么只需要将剩下的8男8女分配在四辆车上；如果不在一辆车上，那么需要从剩下的8男8女中选出2男2女与他们同车，然后再分配剩下的6男6女。\\(\\frac(8 !)^24 ! \\times 2^8+\\left(P_8^2\\right)^2 \\frac(6 !)^23 ! \\times 2^6\\)

延伸2：多重排列与组合

多重排列既可以看作排列的拓展，也可以看作组合的拓展。

例题：\\(2n\\)个物品两两配对（同一组之内两两配对，也就是分组）？分成两组配对呢？若是两组物品，每组\\(n\\)个不同的物品，两两配对呢？

解：（1）分为\\(n\\)组，每组2个。“组”是没有区别的。\\(\\frac(2n !)n ! \\times 2^n\\)

（2）\\(\\frac(2n !)2 ! \\times (n!)^2\\)

（3）记两组分别为A、B，A组的第一个物品和B组的物品配对有n种选择，A组的第二个物品和B组的物品配对有n-1种选择，...，以此类推。共有\\(n!\\)种方案。\\(n!\\)

1.5 圆周排列

定义：从\\(n\\)个对象中取\\(m\\)个沿一圆周的排列，用\\(Q_n^m\\)或\\(Q(n,m)\\)表示

\\(Q_n^m\\)与\\(P_n^m\\)的关系是\\(Q_n^m=\\frac P_n^m m\\)，特别地，有\\(Q_n^n=\\frac P_n^n n=(n-1)!\\)

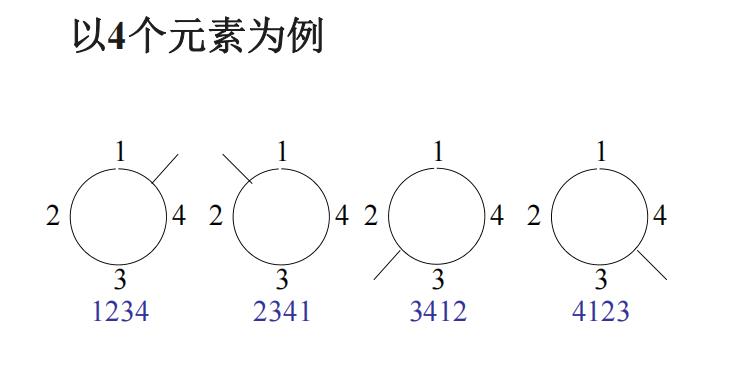
例题：主人夫妇邀请另外三对夫妇共进晚餐，围一圆桌均匀而坐。（1）随意入座。（2）男女相间入座。（3）男女相间入座，且每对夫妻都相邻。（4）男女相间入座，但每对夫妻不全相邻。（5）男女相间入座，但每对夫妻都不相邻。（6）男女相间入座，但主人夫妇不相邻。

解：（1）\\(Q_8^8\\)

（2）\\(Q_4^4 \\times 4 \\times 3 \\times 2 \\times 1\\)

（3）\\(Q_4^4 \\times 2\\)

（4）\\(Q_4^4 \\times 4 \\times 3 \\times 2 \\times 1 - Q_4^4 \\times 2\\)

（5）\\(Q_4^4 \\times 2\\)

（6）\\(Q_4^4 \\times 2 \\times 3 \\times 2 \\times 1\\)

例题：5个红球，6个蓝球，7个黄球串成一个项链，多少种方案？假定同色球无区别。若取其中三个球串成一环，有几种方案？

解：\\(\\frac 18! 5! \\times 6! \\times 7! \\times 18 \\times 2\\)，除以2是因为项链的正反两面是相同的。3个相同颜色：3种；3个不同颜色：1种；3个两种颜色：\\(P(3,2)\\)（一种颜色两个球，一种颜色一个球），共\\(3+1+P_3^2\\)种方案。

例题：\\(n\\)个人围着桌子均匀而坐，如果是正方形的桌子呢？如果是正\\(k\\)边形呢？

解：正方形的桌子，每边都是\\(\\frac n 4\\)人，每边都是全排列，有\\(\\frac P_n^n 4\\)种方案。如果是正\\(k\\)边形的桌子，有\\(\\frac P_n^n k\\)种方案。

1.6 多重组合

定义：多重组合是指从\\(A=\\1,2,...,n\\\\)中取\\(m\\)个元素\\(\\a_1,a_2,...,a_m\\\\)，\\(a_i\\epsilon A\\)，\\(i=1,2,...,m\\)，而且允许\\(a_i=a_j\\)。用\\(\\overlineC_n^m\\)表示。

定理：从\\(n\\)个不同元素中取\\(m\\)个作允许重复的组合，其组合数为\\(C_n+m-1^m\\)

注意：允许重复的组合的典型模型是\\(m\\)个相同的球放进\\(n\\)个不同的盒子里，每个盒子可多于一个球，也可空盒。而后一问题又可以转换为\\(m\\)个相同的球与\\(n-1\\)个相同的盒壁的排列的问题。

易知所求计数为\\(\\frac (n+m-1)! m!(n-1)!=C_n+m-1^m\\)

例题：\\((x+y+z)^4\\)有多少项？

解：问题相当于4个无标志的球放入3个有标志\\(x\\),\\(y\\),\\(z\\)的盒子，根据定理可知有\\(C(3+4-1,4)=C(6,4)=15\\)

定理：线性方程\\(x_1+x_2+...+x_n=m\\)，\\(n\\)和\\(m\\)都是整数，\\(n \\ge 1\\)，则此方程的非负整数解的个数为：\\(C_n+m-1^m\\)，即为简单的整数拆分。

例题：（1）将1000000分解成xyz三个正因数的乘积，有几种方法？（2）将1000000分解成三个相同的正因数的乘积，有几种方法？（3）将1000000分解成三个正因数的乘积，其中恰有两个相同有几种方法？（4）将1000000分解成三个不同的正因数的乘积，有几种方法？

解：\\(100000=2^6 \\cdot 5^6，x=2^x_15^x_2，y=2^y_15^y_2，z=2^z_15^z_2\\)

（1）\\(x_1+y_1+z_1=6，x_2+y_2+z_2=6，(C_3+6-1^6)^2=28^2=784\\)

（2）1种

（3）\\(2x_1+z_1=6，2x_2+y_2=6\\)

\\(x_1\\)	\\(y_1=x_1\\)	\\(z_1\\)	\\(x_2\\)	\\(y_2=x_2\\)	\\(y_2\\)
0	0	6	0	0	6
1	1	4	1	1	4
2	2	2	2	2	2
3	3	0	3	3	0

去掉两边都是2，2，2的情况，还剩\\(4 \\times 4-1=15\\)种

（4）\\(\\frac 784-1-153!=123\\)

例题：20本书放到5个书架上，可以有空架。（1）书有区别，书架有区别，不考虑书顺序。（2）书有区别，书架有区别。（3）书没区别，书架有区别。（4）书有区别，书架有区别，每个书架放4本，不考虑书的顺序。（5）书有区别，书架没区别，每个书架放4本，不考虑书的顺序。（6）书没区别，书架有区别，每个书架放4本。

解：（1）因为不考虑书的顺序，所以任意一本书在5个书架上都可以随便放。\\(5^20\\)

（2）相当于24本书做全排列，其中选4本做书架的隔板隔离成5个书架，隔板没有区别。\\(\\frac 24!5!\\)

（3）\\(C_5+20-1^20=C_24^20\\)

（4）\\(\\frac 20! (4!)^5\\)

（5）\\(\\frac 20! 5!(4!)^5\\)

（6）\\(1\\)

定理：线性方程\\(x_1+x_2+...+x_n=m\\)，\\(n\\)和\\(m\\)都是整数，\\(n \\ge 1\\)，若\\(x_i \\ge 1\\)，则此方程的非负整数解的个数为：\\(C_n+m-n-1^m-n=C_m-1^m-n=C_m-1^n-1\\)。可以理解为\\(m\\)个无区别的球放到\\(n\\)个有区别的盒子里，每个盒子不允许空盒。

例题：将12个红球、1个蓝球和1个绿球分给4个人，每人至少分得1个球，多少种方案？

解：先考虑分蓝球和绿球，当蓝球和绿球分别在两个人手中时，即\\(P_4^2\\)，再分剩下的12个红球，\\(x_1+x_2+x_3+x_4=12,x_1 \\ge 0,x_2 \\ge 0,x_3 \\ge 1,x_4 \\ge 1\\)，再给\\(x_3\\)和\\(x_4\\)各一个红球，问题转换为\\(x_1+x_2+x_3+x_4=10,x_1 \\ge 0,x_2 \\ge 0,x_3 \\ge 0,x_4 \\ge 0\\)，即\\(C_4+10-1^10\\)，此时有\\(P_4^2 \\cdot C_4+10-1^10\\)种方案，也可以理解为，将14个无区别的球给四个人，每人至少一个球，再选择四人中的两人，一人有蓝，一人有绿；同理可得，当蓝球和绿球再一个人手中时，即\\(4\\)种，剩下12个红球\\(x_1+x_2+x_3+x_4=9,x_1 \\ge 0,x_2 \\ge 0,x_3 \\ge 0,x_4 \\ge 0\\)，即\\(C_4+9-1^9\\)，此时有\\(4 \\cdot C_4+9-1^9\\)种方案。综上，共有\\(P_4^2 \\cdot C_4+10-1^10+4 \\cdot C_4+9-1^9=P_4^2 \\cdot C_13^10+4C_12^9\\)种方案。

定理：从\\(A=\\1,2,...,n\\\\)中取\\(m\\)个作不相邻的组合，即不存在相邻两个数\\(j\\)和\\(j+1\\)的组合，球盒模型为有区别的\\(n\\)个球排成一行，从中取\\(m\\)个不相邻的球，其组合数为\\(C_n-r+1^r\\)，

简单的整数有序拆分问题：（1）所谓简单是指整数拆分的每项基数都是1，即\\(5=3\\times1+2\\times1\\)；（2）所谓有序是指拆分出的元素有顺序，即盒子有区别，5=2+3和5=3+2看作不一样。

1.8 组合意义

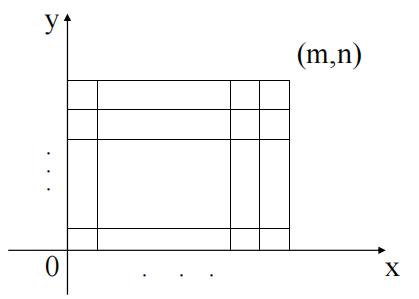
简单格路问题：从(0, 0)点出发沿\\(x\\)轴或\\(y\\)轴的正方向每步走一个单位，最终走到(m, n)点，有多少条路径？

\\[|(0,0) \\rightarrow(\\mathrmm, \\mathrmn)|=\\left(\\beginarrayc\\mathbfm+n \\\\ \\mathbfm\\endarray\\right) \\]

可以用来证明如下公式：

\\[C(n,r)=C(n-1,r-1)+C(n-1,r) \\]

\\[\\left(\\beginarrayc\\mathbfn \\\\ \\mathbfn\\endarray\\right)+ \\left(\\beginarrayc\\mathbfn+1 \\\\ \\mathbfn\\endarray\\right)+ \\left(\\beginarrayc\\mathbfn+2 \\\\ \\mathbfn\\endarray\\right)+ ...+ \\left(\\beginarrayc\\mathbfn+m \\\\ \\mathbfn\\endarray\\right)= \\left(\\beginarrayc\\mathbfn+m+1 \\\\ \\mathbfn+1\\endarray\\right) \\]

\\[\\left(\\beginarrayc\\mathbfn \\\\ \\mathbf0\\endarray\\right)+ \\left(\\beginarrayc\\mathbfn \\\\ \\mathbf1\\endarray\\right)+ \\left(\\beginarrayc\\mathbfn \\\\ \\mathbf2\\endarray\\right)+ ...+ \\left(\\beginarrayc\\mathbfn \\\\ \\mathbfn\\endarray\\right)= 2^n \\]

\\[\\left(\\beginarrayc\\mathbfm+n \\\\ \\mathbfm\\endarray\\right)= \\left(\\beginarrayc\\mathbfm \\\\ \\mathbf0\\endarray\\right) \\left(\\beginarrayc\\mathbfn \\\\ \\mathbf0\\endarray\\right)+ \\left(\\beginarrayc\\mathbfm \\\\ \\mathbf1\\endarray\\right) \\left(\\beginarrayc\\mathbfn \\\\ \\mathbf1\\endarray\\right)+ ...+ \\left(\\beginarrayc\\mathbfm \\\\ \\mathbfm\\endarray\\right) \\left(\\beginarrayc\\mathbfn \\\\ \\mathbfm\\endarray\\right) \\]

例题：从(0,0)点到(m,n)点，其中\\(m\\lt n\\)，要求中间所经过的路径上的点(a,b)恒满足\\(a\\lt b\\)。问有多少种不同的路径？

解：由题知，不接触“对角线”\\(y=x\\)，从(0,0)点的第一步必须到(0,1)点，而不是到(1,0)点。问题可转化为求从(0,1)点到(m,n)点满足要求的路径数。从(0,1)点到(m,n)点的格路，有的接触\\(y=x\\)，有的不接触。对每一条接触\\(y=x\\)的格路\\(S\\)（实线），设最后一个接触点为\\(P_k\\)，做一条从(1,0)到(m,n)的格路（虚线），该格路从(1,0)到\\(P_k\\)的部分与\\(S\\)关于\\(y=x\\)的对称，余下的部分与\\(S\\)重合。

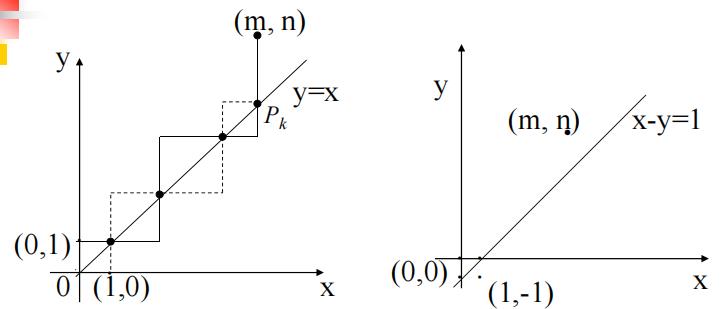
容易看出从(0,1)到(m,n)接触\\(y=x\\)的格路与(1,0)到(m,n)的格路(必穿过\\(y=x\\))一一对应。

则所求的路径数=(0,1)到(m,n)的所有路径数-(1,0)到(m,n)的所有路径数。即\\(\\left(\\beginarrayc\\mathbfm+n-1 \\\\ \\mathbfm\\endarray\\right)-\\left(\\beginarrayc\\mathbfm+n-1 \\\\ \\mathbfm-1\\endarray\\right)\\)

若条件改为可接触但不可穿过，则限制线要向下或向右移一格，即\\(y=x-1\\)，(0,0)关于\\(y=x-1\\)对称的点为(-1,-1)。所求格路数为\\(\\left(\\beginarrayc\\mathbfm+n \\\\ \\mathbfm\\endarray\\right)-\\left(\\beginarrayc\\mathbfm+n \\\\ \\mathbfm-1\\endarray\\right)\\)