2023-03-29 图的深度优先遍历
Posted 空無一悟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2023-03-29 图的深度优先遍历相关的知识,希望对你有一定的参考价值。
图的深度优先遍历
1 数据结构遍历的意义
每种数据结构,都必须有遍历的方式
很多算法的本质都是遍历,对于图论问题,真正理解遍历,已经可以应付80%的问题了
树的遍历 复习
树的深度优先遍历就是指前、中、后序遍历 ps:广度优先遍历实际就是层序遍历,可以参考如下内容:
需要回顾LeetCode上的几个问题
-
二叉树的遍历
前中序序的递归遍历过程和刘老师的画点法模拟二叉树的前中后序遍历的逻辑是一致的,找个二叉树对着前中序的代码好好模拟体会下
- 144.BinaryTree Preorder Traversal 前序遍历
- 94.Binary Tree Inorder Traversal 中序遍历
- 145.Binary Tree Postorder Traversal 后序遍历
- 102.Binary Tree Level Order Traversal 层序遍历
需要记录遍历的层次时类似994腐烂的橘子,每次都需要把上一轮加入的节点一次性全部弹出,然后把下一轮的节点一次性加入到一个新的Lits中作为下一轮的新List;不需要记录层次时就是普通的BFS
-
n叉树的遍历
为什么n叉树的遍历没有中序?
对于二叉树来说,有左右两个孩子,所以如果遍历发生在访问左孩子和右孩子之间,就叫“中序”。
但是,n 叉树有可能有 3 个孩子,10 个孩子,26 个孩子,甚至 100 个孩子。遍历发生在哪里是中间?是遍历完第一个孩子?还是遍历完第 7 个孩子?还是遍历完第 66 个孩子?
很显然,对于 n 叉树来说,我们不能定义一个统一的“中间”的标准了。
所以,n 叉树的遍历,是没有中序遍历的概念的:)
练习题如下:
- 429.N-ary Tree Level Order Traversal n叉树层序遍历
需要记录遍历的层次时类似994腐烂的橘子,每次都需要把上一轮加入的节点一次性全部弹出,然后把下一轮的节点一次性加入到一个新的Lits中作为下一轮的新List;不需要记录层次时就是普通的BFS
2 从树的深度优先遍历,到图的深度优先遍历
树的深度优先遍历就是指前、中、后续遍历(n叉树没中序遍历,二叉树都有),这里以前序遍历为例
左边是二叉树深度优先遍历中的前序遍历,右边是图的深度优先遍历,二者对比如下
- 遍历过程:左边是访问顶点的左右两个字节点;右边是for循环遍历节点的所有相邻子节点,每个节点访问后都会计入到长度为V(顶点数)的布尔数组中
- 递归终止条件:左边的终止条件是
if(node!=null),当递归到一个没有子节点的节点时就会退出递归;右边是for循环遍历完联通图所有节点(if(!visited[w])不满足)后退出

3 DFS代码逻辑的详细解读
递归调用和普通嵌套调用的联系和区别
- 联系:都是函数的嵌套调用
- 区别:嵌套调用是不同函数之间的调用;递归调用是自己和自己的链式调用
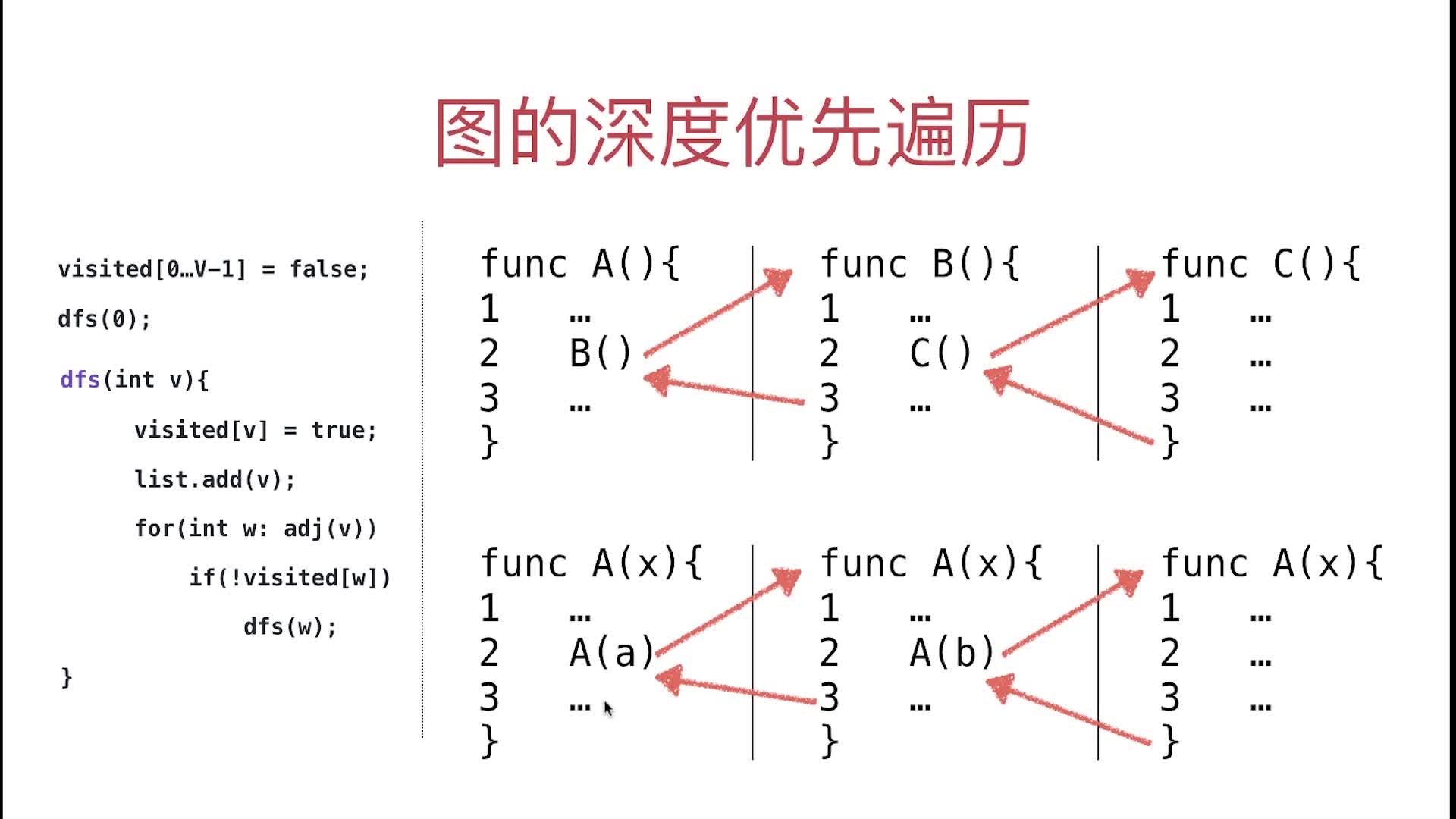
图示如下:
- 上面:
A<---B<---C是普通的嵌套调用 - 下面:
A<---A<---A是递归调用,注意虽然函数相同,但是每层的递归传入的参数都是不同的
举例详解递归调用的过程
注意TreeSet是有序地,所以访问邻接点都是从小到大访问;
visited[i]=true代表该节点已经被访问了;
存储遍历结果的数组叫order
下面每张图片上方的文字是阐述其递归过程的
- 递归到最深层的过程
- 访问0,0放入order数组并设置
visited[0]=true,挂起dfs(0),访问0的邻接点,邻接点有(1, 2) ,先访问到1 - 访问1,1放入order数组并设置
visited[1]=true,挂起dfs(1),访问1的邻接点,邻接点有(0, 3, 4),先访问到0,因为visited[0]=true,所以再访问3 - 访问3,3放入order数组并设置
visited[3]=true,挂起dfs(3),访问3的邻接点,邻接点有(1, 2, 5),先访问到1,因为visited[1]=true,所以再访问2 - 访问2,2放入order数组并设置
visited[2]=true,挂起dfs(2),访问2的邻接点,邻接点有(0, 3, 6),先访问到0,因为visited[0]=true,所以再访问3,因为visited[3]=true,所以再访问6, - 访问6,6放入order数组并设置
visited[6]=true,挂起dfs(6),访问6的邻接点,邻接点有(2, 5) ,先访问到2,因为visited[2]=true,所在再访问5 - 访问5,5放入order数组并设置
visited[5]=true,挂起dfs(5),访问5的邻接点,邻接点有(3, 6) ,先访问到3,因为visited[3]=true,所在再访问6,因为visited[6]=true,5的邻接点都访问完了
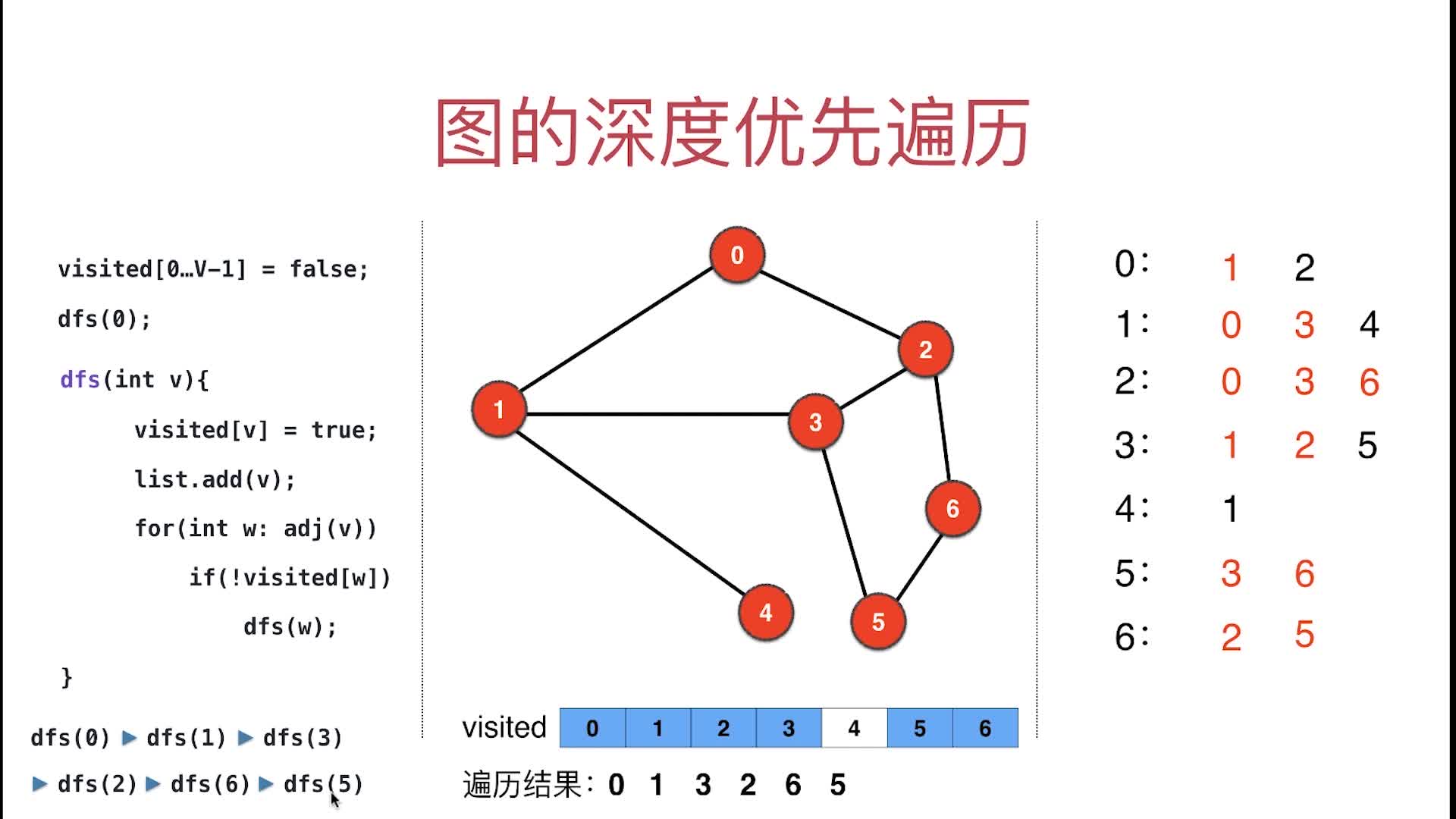
- 访问0,0放入order数组并设置
- 接上面,演示从最深往回递归的过程,回退的过程中在回退前访问过的节点都不会再访问了
- 5的邻接点都访问过了,递归退回到dfs(6),6的邻接点(2, 5) 已经在递归回退前访问完
- 6的邻接点都访问过了,所以回退到dfs(2),2的邻接点(0, 3, 6)已经在递归回退前访问完
- 2的邻接点都访问过了,所以回退到dfs(3),3的邻接点(1, 2, 5)已经在递归回退前访问了(1, 2),所以再访问5,因为
visited[5]=true,所以3的邻接点已经访问完了 - 3的邻接点都访问过了,所以回退到dfs(1),1的邻接点(0, 3, 4)已经在递归回退前访问了(0, 3),所以再访问4
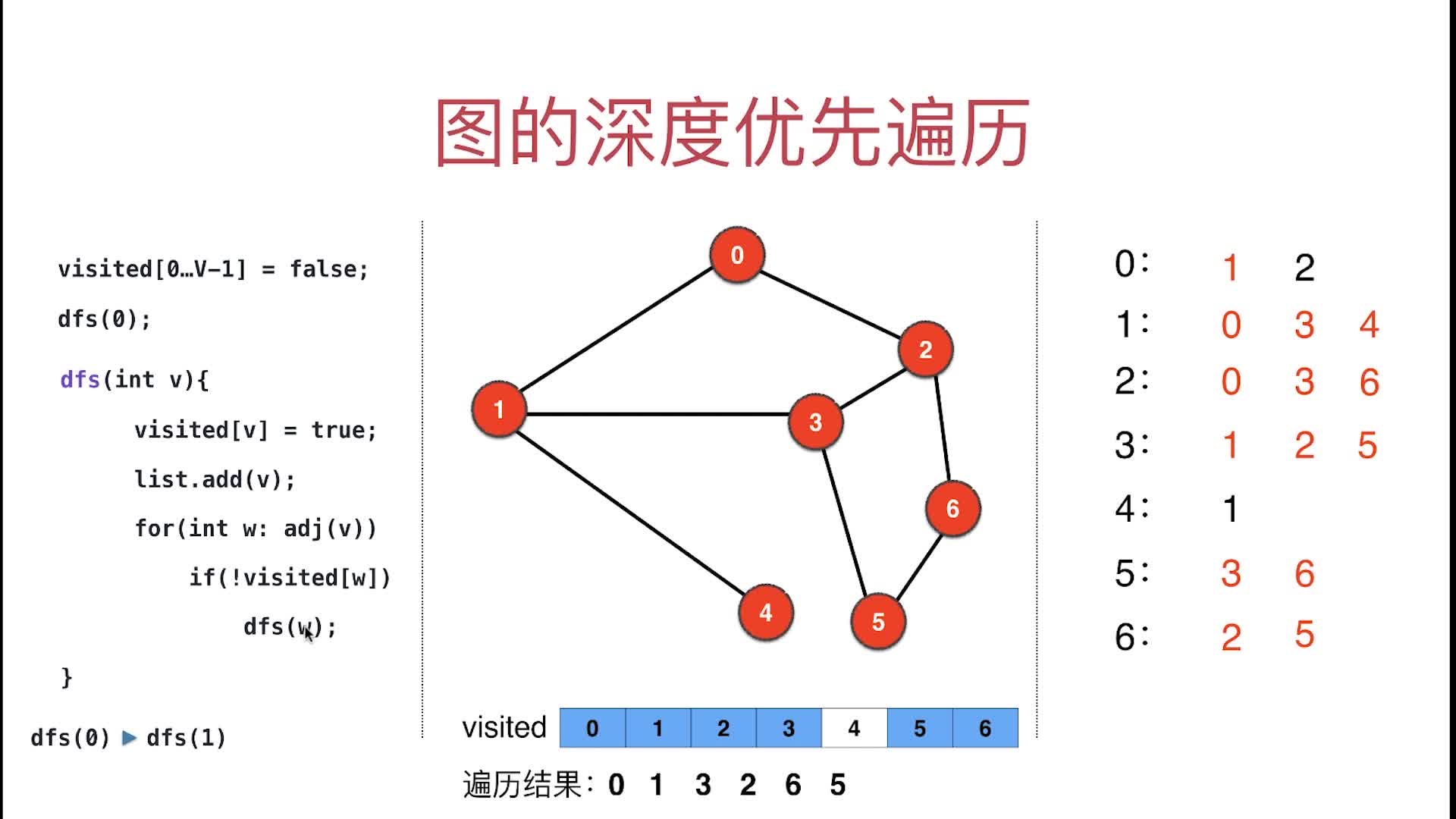
- 访问4,4放入order数组并设置
visited[4]=true,挂起dfs(4),访问4的邻接点,邻接点有(1),先访问到1,因为visited[1]=true,此外4再无邻接点,所以4的邻接点都访问完了
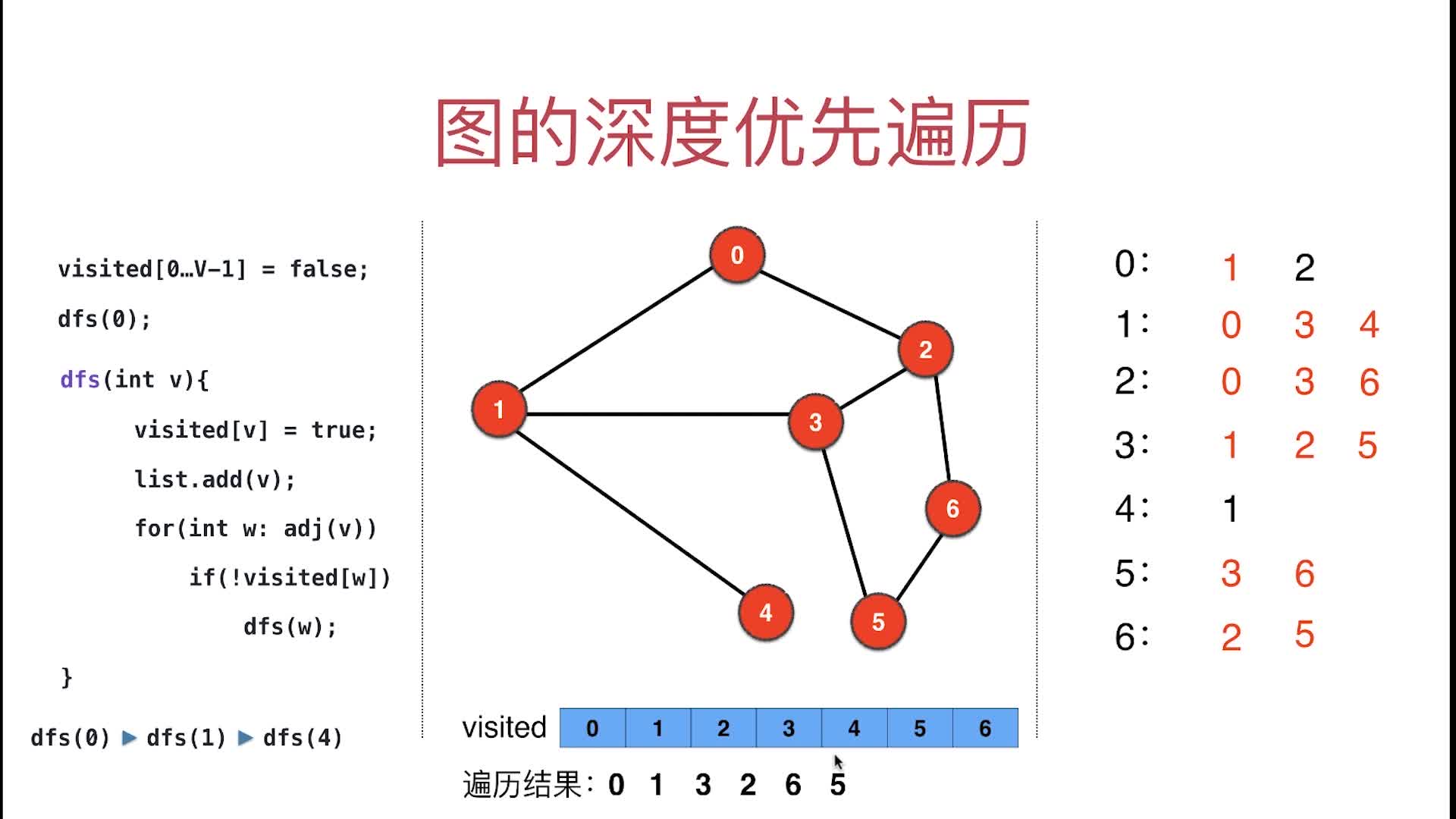
- 4的邻接点都访问过了,所以回退到dfs(1),1的邻接点(0, 3, 6)已经在递归回退前访问完
- 1的邻接点都访问过了,所以回退到dfs(0),0的邻接点(1, 2),1已经在递归回退前访问过,再访问邻接点2,因为
visited[2]=true,所以0的邻接点都访问完了 - 0的邻接点都访问过了,回到递归起点了,递归栈调用完毕,即递归遍历邻接点完毕。order数组中即存放地深度遍历的结果
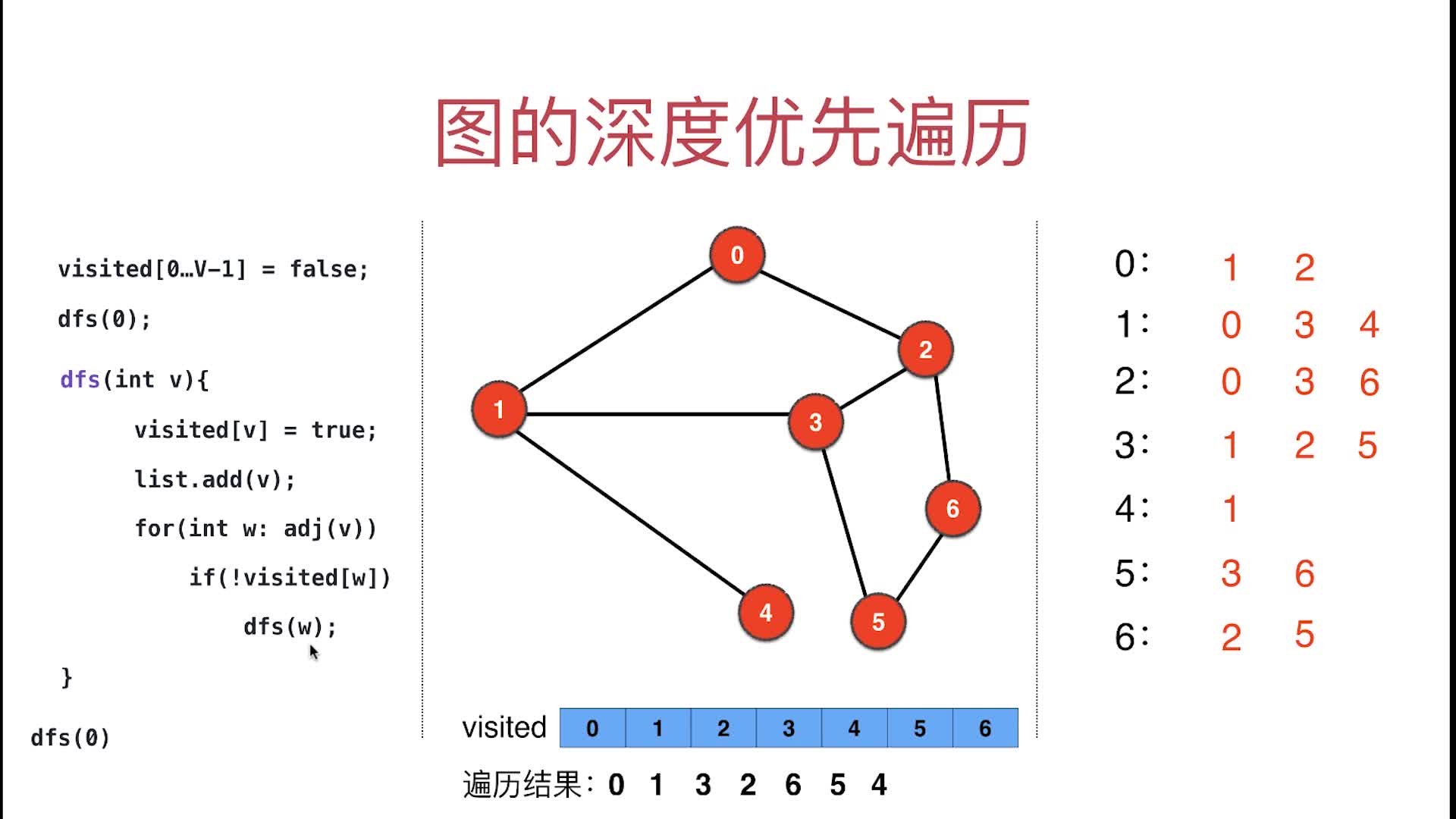
4 图的深度优先遍历(DFS)实现代码
仅支持遍历有一个联通分量的图,多个联通分量想支持需要修改
dfs(0)
5 图的深度优先遍历(DFS)实现代码,改进版本
一、能支持遍历含有多个联通分量的图
写死从0开始执行dfs会导致只能遍历0所在的联通分量,当图有多个联通分量时就不适用了,如下图中的5显然无法遍历到
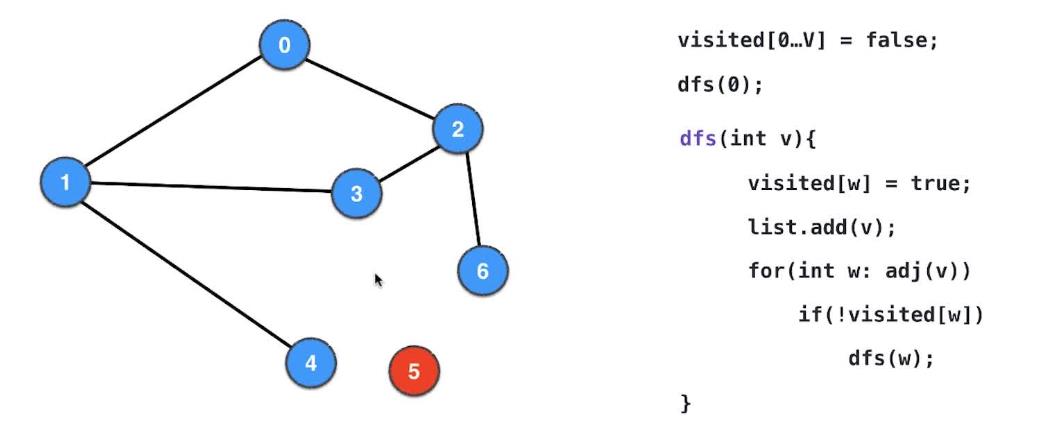
想改进这个问题,需要把构造函数中的
// dfs(0)只能遍历一个联通分量
dfs(0);
修改为:
// 从dfs(0)改成下面的代码,可以支持非连通的图,不用考虑连通分量的时候直接用dfs(v)即可
for (int v = 0; v < graph.V(); v++)
if (!visited[v])
dfs(v);
二、图的DFS也分先序遍历和后续遍历,没有中序遍历,这个点在后面有向图中会用到
想实现后序遍历,只需要把
private void dfs(int v)
visited[v] = true;
orderList.add(v);
for (Integer w : graph.adj(v))
if (!visited[w])
// w点没被访问的话就递归接着访问
dfs(w);
改成
private void dfs(int v)
visited[v] = true;
for (Integer w : graph.adj(v))
if (!visited[w])
// w点没被访问的话就递归接着访问
dfs(w);
orderList.add(v);

6 更多关于图的深度优先遍历
DFS的复杂度
O(V+E)
图的深度优先遍历的应用
- 求图的连通分量
- 求两点间是否可达
- 求两点间的一条路径
- 检测图是否有环
- 二分图检测
- 寻找图中的桥和割点
- 哈密尔顿路径
- 拓扑排序
扩展
- DFS的非递归实现教程
- DFS的非递归实现代码
DFS的递归实现和非递归实现在访问邻接点的顺序上好像不同,前者是从第1个到最后1个,后者是从最后1个到第1个
- 基于邻接矩阵的DFS
以上是关于2023-03-29 图的深度优先遍历的主要内容,如果未能解决你的问题,请参考以下文章