2023-03-28 图的基本表示

Posted 2023-03-28 空無一悟

图的基本表示

1 图的分类

• 无向图 Undirected Graph
• 有向图 Directed Graph
• 无权图 Unweighted Graph
• 有权图 Weighted Graph

方向和权重组合可以得到如下四种常见的图：

优先讲无向无权图

• 无向无权图
• 无向有权图
• 有向无权图
• 有向有权图

2 图的基础概念

• 顶点 Vertex
• 边 Edge
• 点的邻边
• 路径Path
• 环Loop：一个图中，一个顶点沿着某条路径出发可以回到自己，这条路径称为环
• 无环图：没有环的图,可以看做一棵树，其实树可以看做是一种无环图

  但是无环图不一定是树，比如多个不联通的分量组成的图

• 自环边：自己指向自己的边
• 平行边：两个点之间有两条边，可以认为是互相平行地，即平行边
• 简单图：没有自环边也没有平行边的图，本课程中讨论地图都是简单图
• 联通分量：一个图中相互连接并可以相互抵达的子图称为联通分量，注意：
  • 一个图中的所有节点不一定全部相连
  • 一个图中可能有多个联通分量
• 连通图的生成树：包含原图所有的顶点但是不联通的一棵树(边数是v-1)
  • 求最小生成树是很常见的问题
  • 包含所有顶点，边数是v-1，不一定是连通图的生成树，可以是有多个联通分量
  • 一个图一定有生成树吗？否。联通图才有生成树,多个联通分量的生成树集合我们一般叫生成森林，所以一个图一定有生成森林的说法是正确的
• 一个顶点的度degree
  • 对于无向图，就是指这个顶点相邻的边数
  • 对于有向图，根据边的方向分为入度和出度

3 图的基本表示：邻接矩阵

邻接矩阵的图示

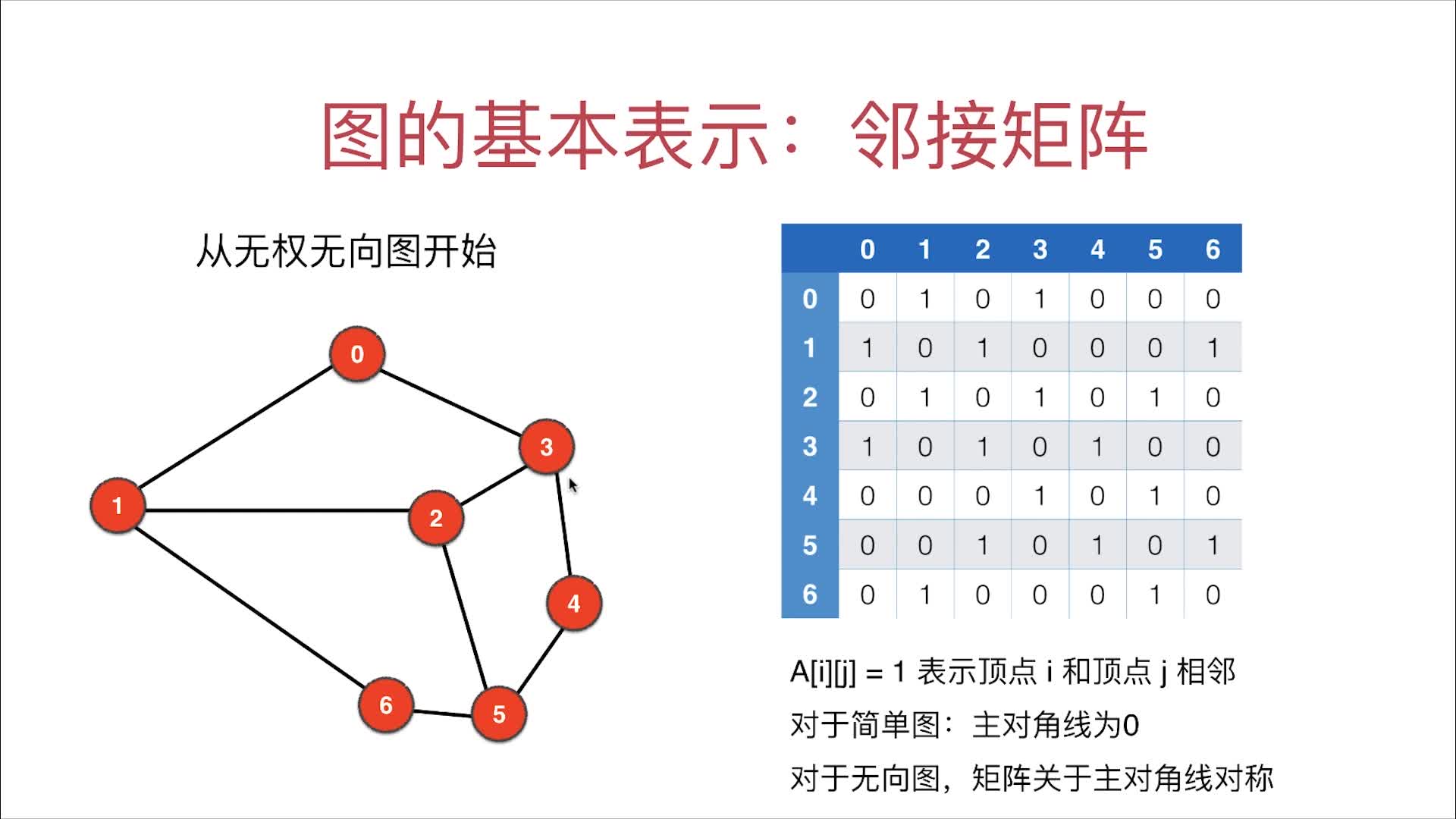
邻接矩阵的数据来源graph.txt的解析

第一行的V是vertices(vertex的复数)即顶点数目；E是Edges即边数。第2行往后是各个边的连接情况(两端连接点)

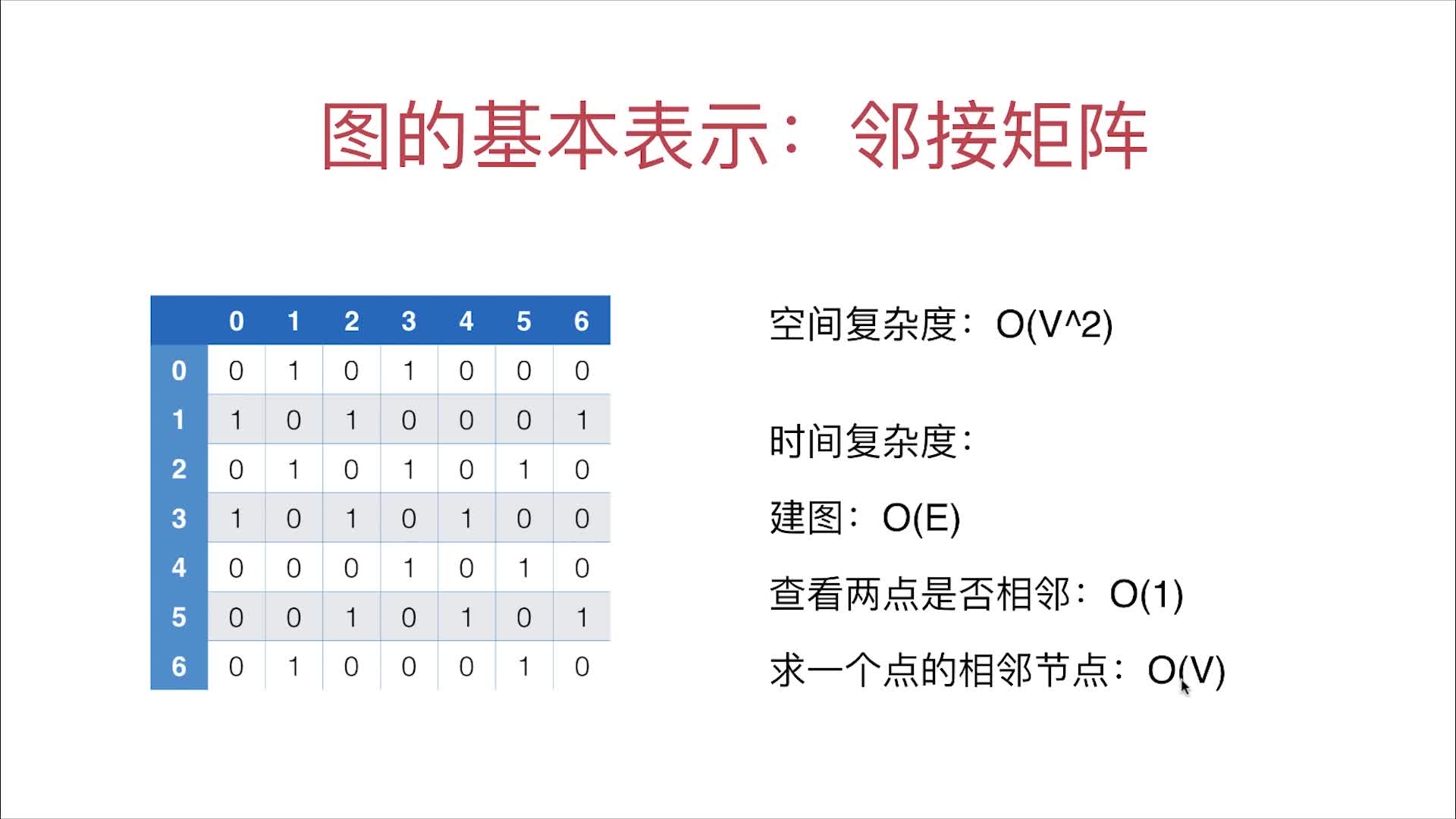
邻接矩阵的各种复杂度

图的存储结构：邻接矩阵与邻接表（稠密图与稀疏图）

平时遇到的图多是稀疏图，用邻接表表示，邻接矩阵用于稠密图

• 稠密图用 邻接矩阵存储
• 稀疏图用 邻接表存储

原因：

• 邻接表只存储非零节点，而邻接矩阵则要把所有的节点信息(非零节点与零节点)都存储下来。
• 稀疏图的非零节点不多，所以选用邻接表效率高，如果选用邻接矩阵则效率很低，矩阵中大多数都会是零节点！
• 稠密图的非零节点多，零节点少，选用邻接矩阵是最适合不过！

4 邻接矩阵的代码实现

这里忽略吧，不放代码了。平时基本都用基于TreeSet的邻接表的实现

5 图的基本表示：邻接表

邻接表是稀疏图的表示方法

邻接表的图示

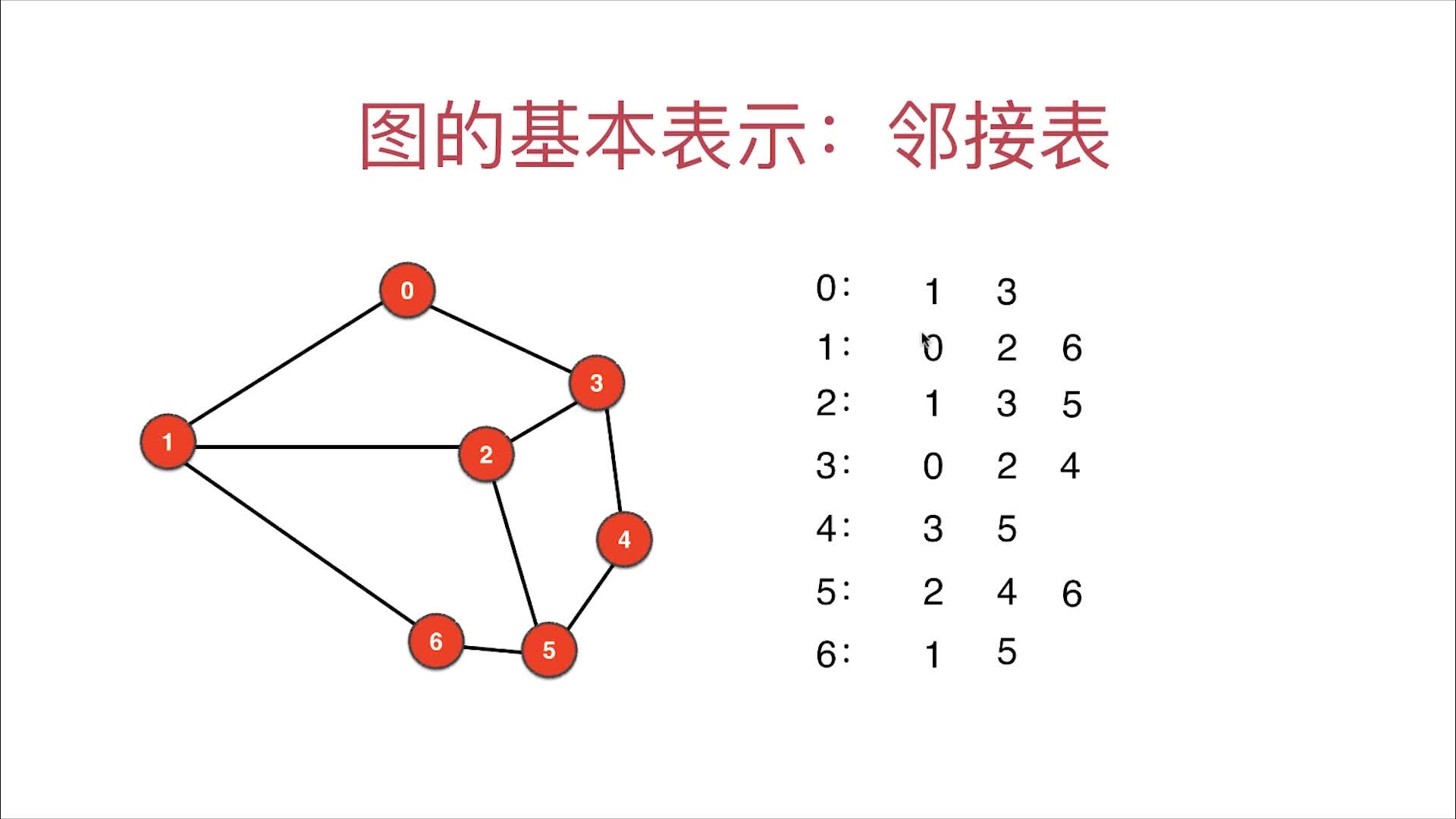
当图的顶点不是从0开始的连续正整数时改咋办？

https://coding.imooc.com/learn/questiondetail/133447.html

如果不连续，或者在一些情况下，顶点根本不是数字，比如是字符串，应该先把他们映射成为连续的顶点。
你可以理解成，就是把所有顶点编号，反正每个顶点肯定不同，从0到n-1，总能映射成为连续的顶点的。
当然了，在这这种情况下，应该在有一个反向映射机制，通过顶点的序号，也能找回原始表示这些顶点的内容(数字或者字符串)
可以用map来实现，键是索引，值是顶点名。中间处理过程还是用我们封装好的代码，等到对外展示的时候映射到实际的名称即可
比如下面的函数和addEdge函数

public void show() 
    // 遍历所有顶点vertex(顶点都是按照编号顺序来地)，顶点是用从0开始的连续正整数表示时v才代表顶点，
    // 如果顶点不是用连续的正整数或者是用字符等形式来表示时，就要建立顶点数下标v和顶点实际含义的映射关系了，可以用map来表示，要显示的时候统一用map
    // 参考 https://coding.imooc.com/learn/questiondetail/133447.html
    // vertices是vertex的复数形式，两者都是顶点的意思
    for (int v = 0; v < vertices; v++) 
        System.out.print("vertex " + v + ":\\t");
        // 遍历顶点vertex的所有邻接点
        for (Integer w : adj[v]) 
            System.out.print(w + "\\t");
        
        System.out.println();
    

8 图实现(基于邻接表)的改进

图表示(基于TreeSet邻接表)的表示的最终代码

源于刘宇波老师的图论课 https://coding.imooc.com/lesson/370.html#mid=27328

代码见Part1Basic/JAVA/src/main/java/Chapter7GraphBasics/Section4ReadGraphOptimize

• 边的编号不能超过边的总数vertices,要加校验,最好整理成校验函数

  public void validateVertex(int v) 
      assert (v >= 0 && v < vertices);
  
  

• 稀疏图的邻接表实现改进:Vector或LinkedList换成TreeSet，把查询邻接表的时间复杂度从O(n)提高到了O(logN),而且元素还是有序地，对性能要求高地话还可以用HashSet，就是邻接表输出是无序地了

   private TreeSet<Integer>[] adj;
  

• 添加degree()函数，用于统计图里每个定点的度(即每个定点有几个邻边)

  // 稀疏图，adj是TreeSet
  public int degree(int v) 
      return adj[v].size();
  
  

  // 稠密图，adj是二维数组
  public int degree(int v) 
      return adj[v].length;
  
  

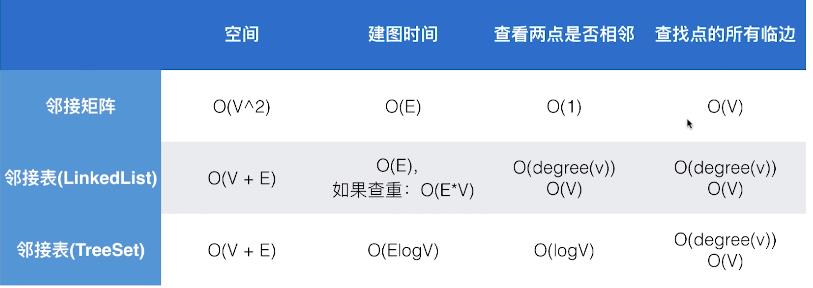
9 图的多种表示方法和实现的比较

从下面的比较图可以看出，第3种实现最优，所以后面所有的图都会用基于TreeSet的邻接表来表示,O(V+E)实际是O(V+2E)的简化

最终的最优化图表示代码

方案：基于TreeSet的邻接表表示

图表示(基于TreeSet邻接表)的最终最优代码