LeetCode动态规划#02图解不同路径I + II(首次涉及二维dp数组,)
Posted DAYceng
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode动态规划#02图解不同路径I + II(首次涉及二维dp数组,)相关的知识,希望对你有一定的参考价值。
不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

- 输入:m = 3, n = 7
- 输出:28
示例 2:
- 输入:m = 2, n = 3
- 输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
示例 3:
- 输入:m = 7, n = 3
- 输出:28
示例 4:
- 输入:m = 3, n = 3
- 输出:6
提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 10^9
思路
题意没什么好分析的,就是从起始点到终点有多少种走法
直接上五部曲分析
五步走
1、确定dp数组含义
从题干和所给示例可以得出
dp[i][j]:从[0] [0]出发走到[i] [j]有dp[i][j]种走法
2、确定递推公式
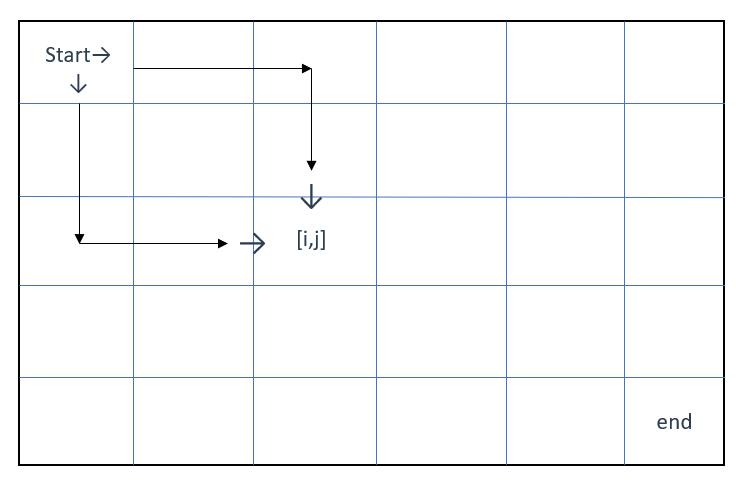
如图所示
根据dp数组的定义,
从[0] [0]出发走到[i] [j]上方(也就是[i] [j-1])有dp[i][j-1]种走法,其再往下走一步就可以到[i] [j](即等于dp[i][j])
从[0] [0]出发走到[i] [j]左侧(也就是[i-1] [j])有dp[i-1][j]种走法,其再往右走一步就可以到[i] [j]
(注意,以dp[i][j-1]为例,它指的是 走法 而不是走了几步,因此再往下走,不是dp[i][j-1] + 1)
因为题目说了每次只能向下或向左移动一步,所以上面的分析就已经把所有到达[i] [j]的可能路径表示出来了
即到达[i] [j]的路径种类等于从其上方到达的方式加上从其左边到达的方式
也就是:dp[i][j] = dp[i][j-1] + dp[i-1][j]
3、确定dp数组初始化方式
dp[i][j-1]是到达[i] [j]上方的所有路径,那么其一定使用了最上方部分(绿色)
同理,在推导dp[i-1][j]时也使用到了最左侧的部分(橙色)
那么,这两块区域就是我们要初始化的对象,即dp[0],[j]和dp[i],[0]
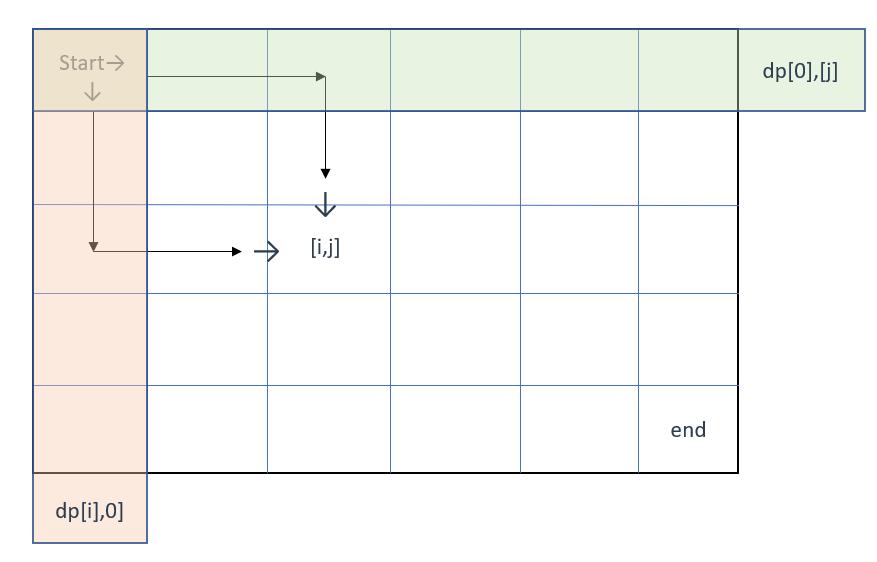
那么,初始值是多少呢?
还是联系dp数组的定义,我们发现,在最上方的绿色部分前进时,无论在哪一格、怎么走都只有一种方式前进(就是往右)
(因为题目规定只能往右或下走)
橙色的部分同理
因此绿色和橙色部分的每一个格子的dp值其实都是1,意味着不论从这两个区域中的哪一格出发,都只有一种前进方式
所以可以把dp[0],[j]和dp[i],[0]全部初始化为1
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
4、确定遍历方式
因为只能往右或者下走,那前进顺序就是从左往右或者从上到下了
自然的,这也就是遍历的顺序
这样,在从左往右时,遍历的每一个格才能利用左边的上一个格来进行推导,从上到下同理
代码
这里创建的dp数组是二维的,结构如下:(举例)
m行->([0,0,0,0]为一行)
[[0,0,0,0], n列↓
[0,0,0,0],
[0,0,0,0],
[0,0,0,0],
[0,0,0,0]]
class Solution
public:
int uniquePaths(int m, int n)
//定义dp数组(先使用0初始化数组)
vector<vector<int>> dp(m, vector<int>(n, 0));
//初始化dp[i][0]和dp[0][j]
for(int i = 0; i < m; ++i) dp[i][0] = 1;
for(int j = 0; j < n; ++j) dp[0][j] = 1;
//遍历
for(int i = 1; i < m; ++i)//[0,0]已经初始化了,因此i、j都需要从1开始
for(int j = 1; j < n; ++j)
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];//递推公式
return dp[m - 1][n - 1];//注意,这里需要减1,因为数组是从0开始数的,而mn是从1开始的
;
不同路径II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
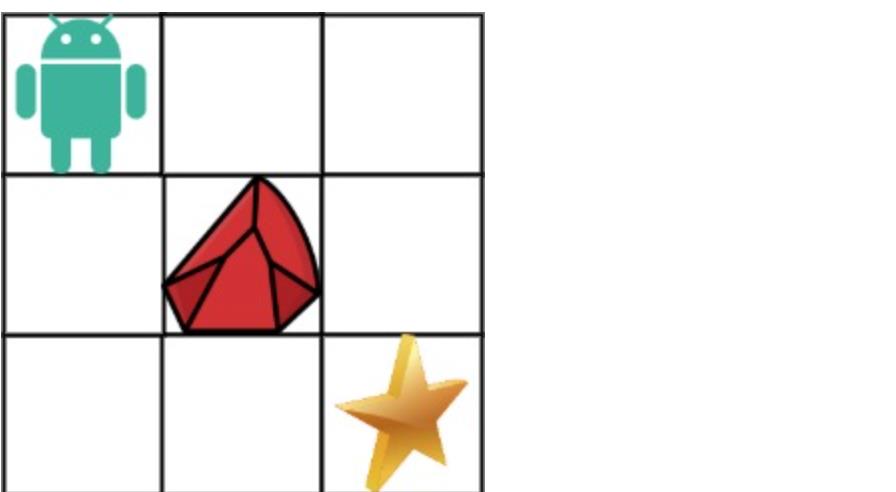
- 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
- 输出:2 解释:
- 3x3 网格的正中间有一个障碍物。
- 从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:

- 输入:obstacleGrid = [[0,1],[0,0]]
- 输出:1
提示:
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i] [j] 为 0 或 1
思路
这题是在上题的基础上增加了障碍物,主要区别在状态转换方程和dp数组初始化上
并且需要注意的是,本题是直接给了网格并在上面注明类障碍物的位置(0无障碍,1有障碍)
直接开始
五步走
1、确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2、确定递推公式
这里递推公式的核心部分和上题一样,但是需要增加额外的条件
当遇到障碍时,障碍后面的路径就没有办法走到了,因此需要保持为0
if(obstacleGrid[i][j] == 0)//没遇到障碍物时就正常计算dp数组的值
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
3、确定dp数组初始化方式
因为引入了障碍,初始化方式会有所变化
还是拿之前的图来看
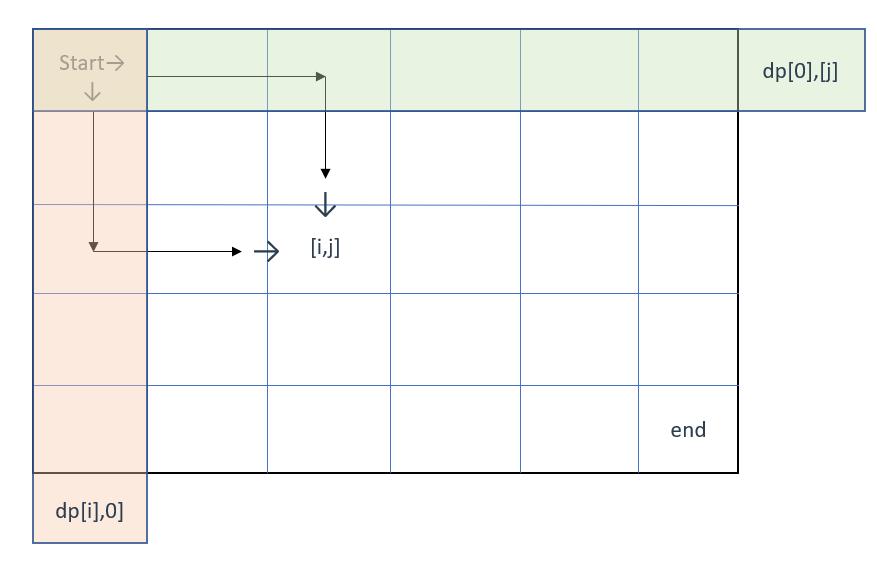
如果绿色和橙色部分(需要初始化的地方)有障碍物,那么从障碍物起,之后的位置都将标记为0,因为那些地方再也去不到了
(因为只能往右或下走)
于是初始化时需要加入条件
在上一题中,我们给出的初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));//初始值为0
if(int i = 0; i < m; ++i) dp[i][0] = 1;
if(int j = 0; j < n; ++j) dp[0][j] = 1;
本题中需要在for循环的结束条件中做改动
vector<vector<int>> dp(m, vector<int>(n, 0));//初始值为0
if(int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) dp[i][0] = 1;
if(int j = 0; j < n && obstacleGrid[0][j] == 0; ++j) dp[0][j] = 1;
即在初始化绿色部分时,如果没遇到障碍物,正常初始化赋值;如果遇到了,就终止for循环,之后的位置保持值为0
(橙色部分同理)
4、确定遍历顺序
仍然是从左到右、从上到下,但在遍历过程中如果遇到障碍物,需要continue一下
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
5、打印dp数组
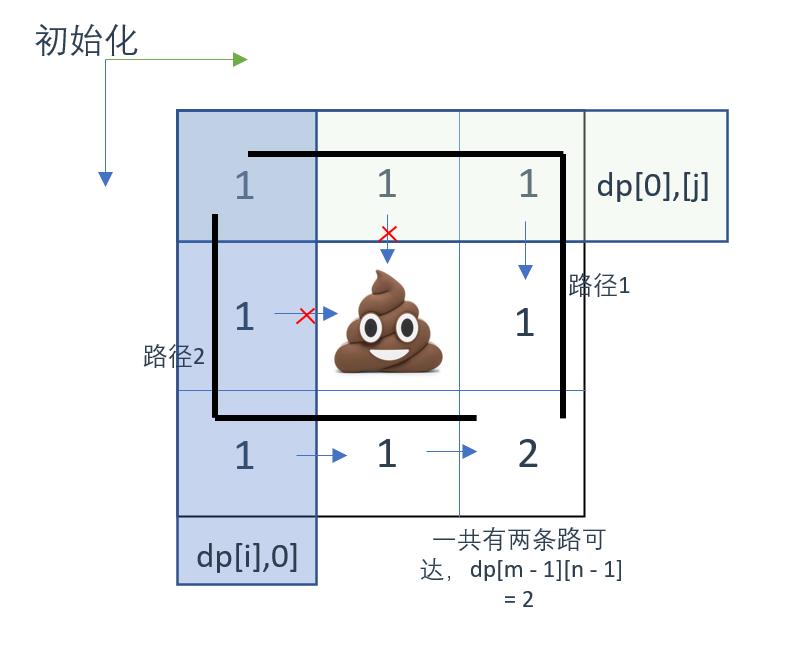
因为本题的逻辑相较于上题复杂了一些,所以有必要自己推算一下dp数组来确保结果的正确性
用示例1举例:

dp数组手动推导如图所示
完整代码
class Solution
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
//创建dp数组
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
//如果在起点/终点出现障碍,直接返回0
if(obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
//初始化dp数组
for(int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) dp[i][0] = 1;
for(int j = 0; j < n && obstacleGrid[0][j] == 0; ++j) dp[0][j] = 1;
//遍历
for(int i = 1; i < m; ++i)
for(int j = 1; j < n; ++j)
if(obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m - 1][n - 1];
;
注意:复制某些重复代码时,记得要修改完所有的对应值!!!
以上是关于LeetCode动态规划#02图解不同路径I + II(首次涉及二维dp数组,)的主要内容,如果未能解决你的问题,请参考以下文章