视觉SLAM第四讲李群与李代数习题
Posted programmerwang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了视觉SLAM第四讲李群与李代数习题相关的知识,希望对你有一定的参考价值。
视觉SLAM第四讲李群与李代数习题
一、验证\\(SO(3)、SE(3)、SIM(3)\\)关于乘法成群
首先引入一下群的定义。
群 (Group) 是一种集合加上一种运算的代数结构。我们把集合记作 \\(A\\), 运算记作 \\(.\\),那么一个群可以记作 \\(G=(A, \\cdot)\\) 。群要求这个运算满足以下几个条件:
封闭性: \\(\\forall a_1, a_2 \\in A, \\quad a_1 \\cdot a_2 \\in A\\).
结合律: \\(\\forall a_1, a_2, a_3 \\in A, \\quad\\left(a_1 \\cdot a_2\\right) \\cdot a_3=a_1 \\cdot\\left(a_2 \\cdot a_3\\right)\\).
么元: \\(\\exists a_0 \\in A\\), s.t. \\(\\forall a \\in A, \\quad a_0 \\cdot a=a \\cdot a_0=a\\).
逆: \\(\\forall a \\in A,\\quad \\exists a^-1 \\in A, \\quad\\) s.t. \\(a \\cdot a^-1=a_0\\).
- 首先验证 \\(SO(3)\\)关于乘法成群
封闭性:
设任意\\(R_1,R_2 \\in SO(3)\\),则有:
此时,\\(R_1,R_2\\)的乘法结果属于正交矩阵得证;
此时,\\(R_1,R_2\\)的乘法结果行列式值为1得证;
综上,对于任意\\(R_1,R_2 \\in SO(3)\\),有\\(R_1R_2 \\in SO(3)\\)。
结合律:
由于矩阵乘法是满足结合律的,所以有:
么元:
对于单位矩阵\\(I \\in SO(3)\\),容易证明其是么元。
任意\\(R \\in SO(3)\\)
逆:
根据\\(SO(3)\\)的定义,容易验证,对于任意的\\(R \\in SO(3),\\exist (R^T = R^-1)\\in SO(3)\\),使得\\(RR_-1 = I\\)。
- 验证 \\(SE(3)\\)关于乘法成群\\[SE(3) = \\\\mathbfT = \\beginbmatrix \\mathbfR & \\mathbft\\\\ \\mathbf0 & 1 \\endbmatrix \\in \\mathbbR^4\\times 4 | \\mathbfR \\in SO(3), \\mathbft\\in \\mathbbR^3 \\ \\]
封闭性:
设任意\\(\\mathbfT_1 = \\beginbmatrix \\mathbfR_1 & \\mathbft_1\\\\ \\mathbf0 & 1 \\endbmatrix,\\mathbfT_2 = \\beginbmatrix \\mathbfR_2 & \\mathbft_2\\\\ \\mathbf0 & 1 \\endbmatrix\\),则有:
由上一题的证明,有\\(R1R_2 \\in SO(3)\\),根据矩阵维数得到$R_1t_2+t_1 \\in\\mathbbR^3 $
所以,\\(T_1T_2 \\in SE(3)\\)
结合律:
由于矩阵乘法是满足结合律的,所以有:
么元:
对于单位矩阵\\(I \\in SE(3)\\),容易证明其是么元。
任意\\(T \\in SE(3)\\)
逆:
根据\\(SE(3)\\)的定义,对于任意\\(\\mathbfT = \\beginbmatrix \\mathbfR & \\mathbft\\\\ \\mathbf0 & 1 \\endbmatrix \\in SE(3)\\),我们设\\(T\' = \\beginbmatrix \\mathbfR^-1 & \\mathbf-R^-1t\\\\ \\mathbf0 & 1 \\endbmatrix \\in SE(3)\\),
容易验证$TT\' = I $
-
验证\\(SIM(3)\\)关于乘法成群
\\(SIM(3)\\),就是在\\(T\\)的基础上添加了一个尺度变化因子\\(s\\)。
其证明\\(SE(3)\\)类似,不再赘述。
二、验证\\((\\mathbbR^3,R,\\times)\\)构成李代数
首先引入一下李代数的定义。
李代数由一个集合\\(V\\),一个数域\\(F\\),一个二元运算\\([,]\\)组成,如果满足下面的条件,则称 \\((\\mathbbV, \\mathbbF,[,])\\) 为一个李代数。
李代数满足如下性质:
封闭性
\\(\\forall X, Y \\in \\mathbbV, 有[X,Y] \\in \\mathbbV\\) ,
双线性
\\(\\forall X, Y,Z \\in \\mathbbV, a,b \\in \\mathbbF\\) ,有:
\\[[a \\boldsymbolX+b \\boldsymbolY, \\boldsymbolZ]=a[\\boldsymbolX, \\boldsymbolZ]+b[\\boldsymbolY, \\boldsymbolZ], \\quad[\\boldsymbolZ, a \\boldsymbolX+b \\boldsymbolY]=a[\\boldsymbolZ, \\boldsymbolX]+b[\\boldsymbolZ, \\boldsymbolY] \\]
自反性
\\(\\forall \\boldsymbolX \\in \\mathbbV,[\\boldsymbolX, \\boldsymbolX]=\\mathbf0\\),
雅可比等价
\\(\\forall X, Y, Z \\in \\mathbbV,[X,[Y, Z]]+[Z,[\\boldsymbolX, \\boldsymbolY]]+[\\boldsymbolY,[\\boldsymbolZ, \\boldsymbolX]]=0\\).


三、验证$ \\text so (3) 和 \\mathbfs e(3) $属于李代数
这个和第二题类似,对于\\(so(3)\\)来说,它是定义在\\(\\mathbbR^3\\)上的向量,我们记作:\\(\\phi\\),其李括号是
然后安装第二题的思路,以此证明即可。
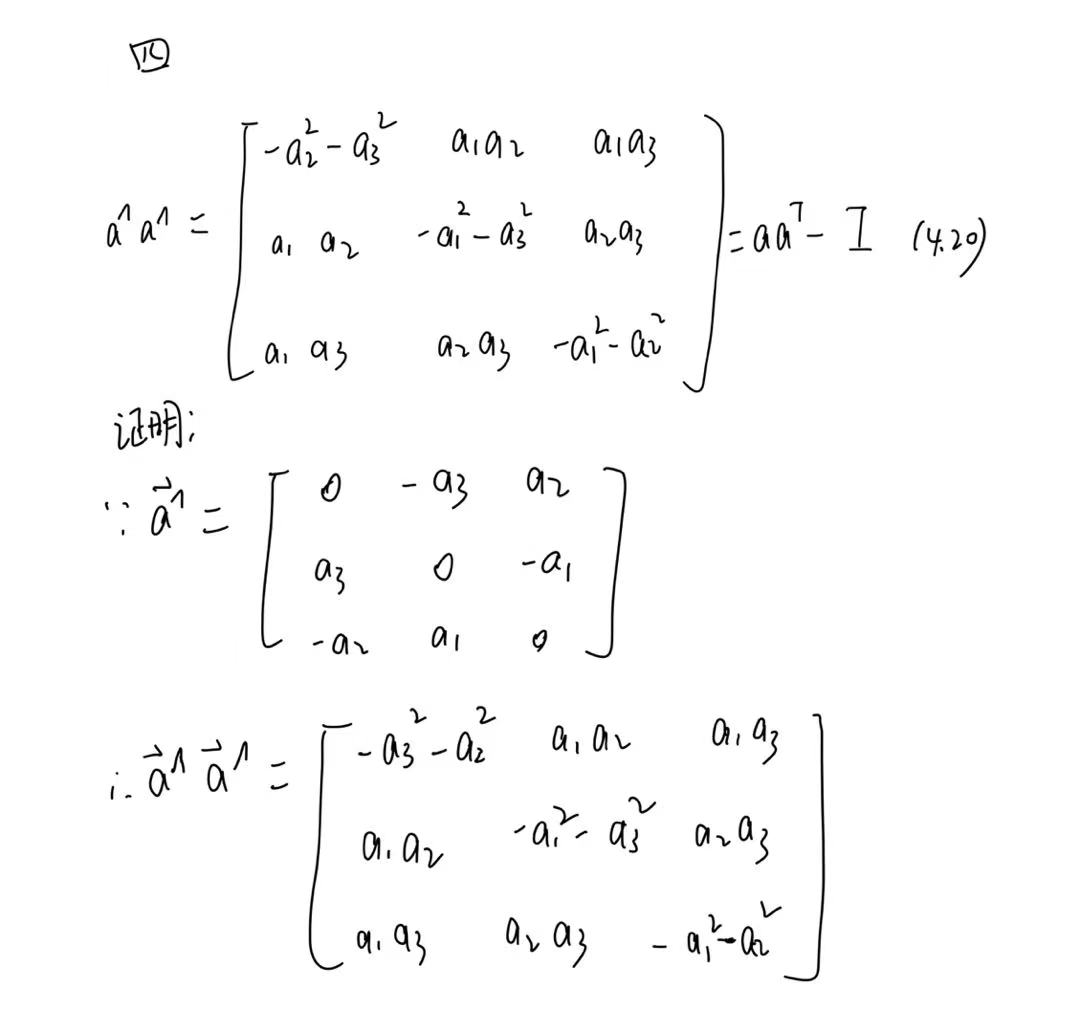
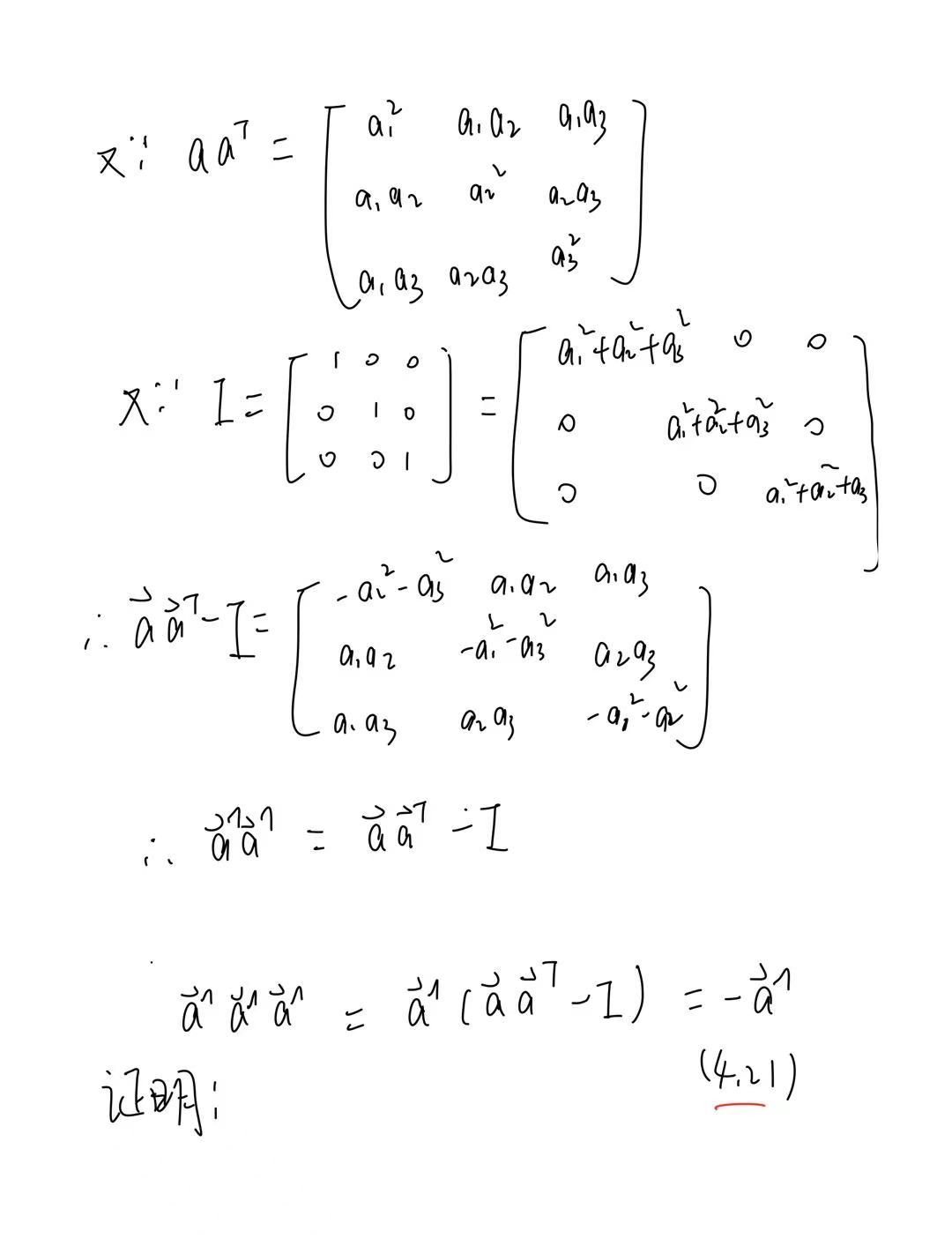
四、验证(4.20)和(4.21)

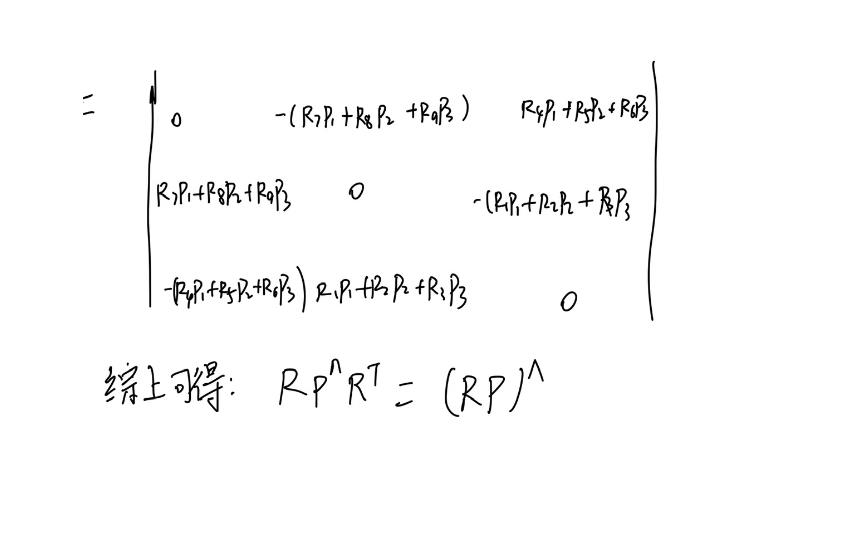
五、证明\\(R \\hatpR^T = (R\\hatp)\\)

六、\\(\\text 证明SO(3)的伴随性质 \\operatornameRexp(\\hatp) R^T=\\exp ((\\hatR p))\\)

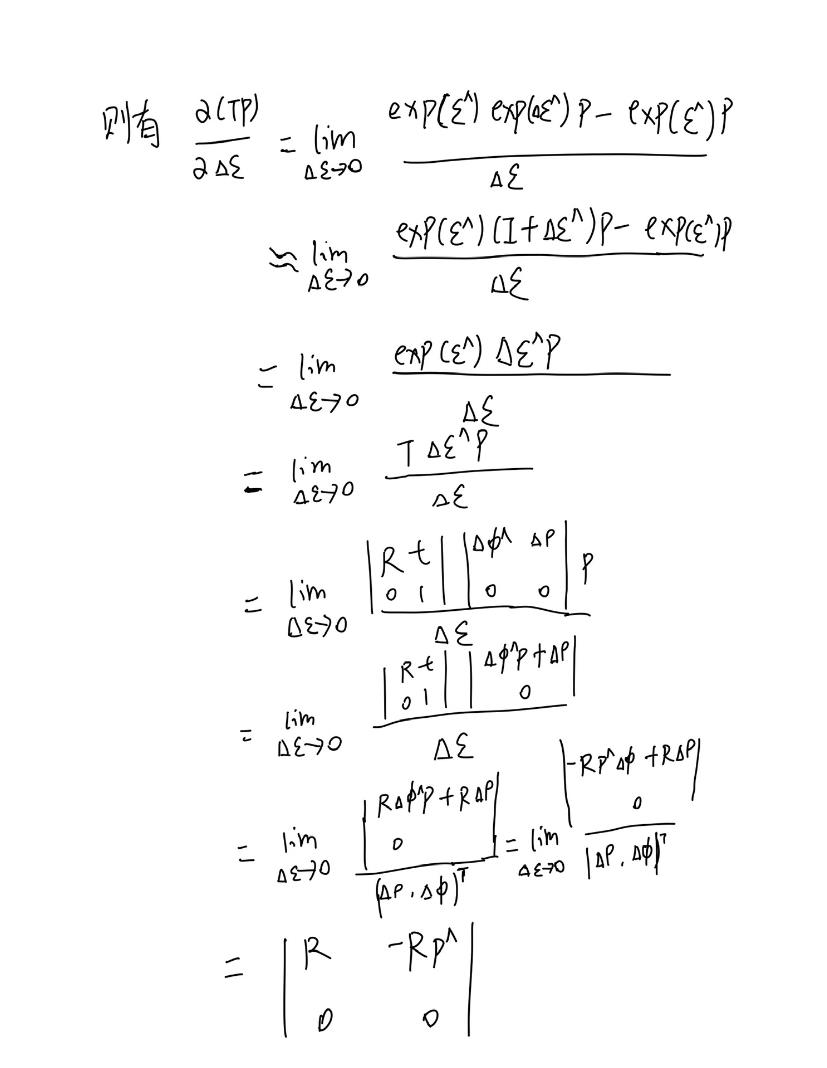
七、仿照左扰动的推导,推导SO(3)和SE(3)在右扰动下的导数。

本文来自博客园,作者:CuriosityWang,转载请注明原文链接:https://www.cnblogs.com/programmerwang/p/17251007.html
以上是关于视觉SLAM第四讲李群与李代数习题的主要内容,如果未能解决你的问题,请参考以下文章