数论模板

Posted 2023-02-16 EndPB

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数论模板相关的知识，希望对你有一定的参考价值。

数学

配合oiwiki:

https://oi-wiki.org/math/

位运算

int __builtin_ffs(int x)：返回 x 的二进制末尾最后一个 1 的位置，位置的编号从 1 开始（最低位编号为 1 ）。当 x 为 0 时返回 0 。
int __builtin_clz(unsigned int x) ：返回 x 的二进制的前导 0 的个数。当 x 为 0 时，结果未定义。
int __builtin_ctz(unsigned int x) ：返回 x 的二进制末尾连续 0 的个数。当 x 为 0 时，结果未定义。
int __builtin_clrsb(int x) ：当 x 的符号位为 0 时返回 x 的二进制的前导 0 的个数减一，否则返回 x 的二进制的前导 1 的个数减一。
int __builtin_popcount(unsigned int x) ：返回 x 的二进制中 1 的个数。
int __builtin_parity(unsigned int x) ：判断 x 的二进制中 1 的个数的奇偶性。

可以在函数名末尾添加ll如__builtin_popcountll以操作long long

如果需要操作的集合非常大，可以使用 bitset

bitset

可视为多位二进制数

n位bitset执行一次位运算的时间复杂度可视为n/32

同样支持 ~ | ^ & >> << == != 等操作符,可以用 [] 查询

s.count() 返回二进制串中有多少个1；

s.set()把s所有位变为1；

s.set(k,v)把s的第k位改为v,即s[k]=v；

s.reset()把s的所有位变为0.

s.reset(k)把s的第k位改为0,即s[k]=0；

s.flip()把s所有位取反.即s=~s；

s.flip(k)把s的第k位取反，即s[k]^=1；

高精度

https://oi-wiki.org/math/bignum/

const int LEN = 1004;
void clear(int a[]) 
    for (int i = 0; i < LEN; ++i) a[i] = 0;

void read(int a[]) 
    string s;
    cin>>s;
    clear(a);
    int len = s.size();
    for (int i = 0; i < len; ++i) a[len - i - 1] = s[i] - \'0\';

void print(int a[]) 
    int i;
    for (i = LEN - 1; i >= 1; --i)
        if (a[i] != 0) break;//忽略前导0
    for (; i >= 0; --i) putchar(a[i] + \'0\');

void add(int a[], int b[], int c[]) 
    clear(c);
    for (int i = 0; i < LEN - 1; ++i) 
        c[i] += a[i] + b[i];
        if (c[i] >= 10) 
            c[i + 1] += 1;
            c[i] -= 10;
        
    

void sub(int a[], int b[], int c[]) 
    clear(c);
    for (int i = 0; i < LEN - 1; ++i) 
        c[i] += a[i] - b[i];
        if (c[i] < 0) 
            c[i + 1] -= 1;
            c[i] += 10;
        
    

void mul(int a[], int b[], int c[]) 
    clear(c);
    for (int i = 0; i < LEN - 1; ++i) 
        for (int j = 0; j <= i; ++j) c[i] += a[j] * b[i - j];
        if (c[i] >= 10) 
            c[i + 1] += c[i] / 10;
            c[i] %= 10;
        
    

inline bool greater_eq(int a[], int b[], int last_dg, int len) 
    if (a[last_dg + len] != 0) return true;
    for (int i = len - 1; i >= 0; --i) 
        if (a[last_dg + i] > b[i]) return true;
        if (a[last_dg + i] < b[i]) return false;
    
    return true;

void div(int a[], int b[], int c[], int d[]) //a/b=c,a%b=d
    clear(c);
    clear(d);
    int la, lb;
    for (la = LEN - 1; la > 0; --la)
        if (a[la - 1] != 0) break;
    for (lb = LEN - 1; lb > 0; --lb)
        if (b[lb - 1] != 0) break;
    if (lb == 0) 
        puts("> <");
        return;
    
    for (int i = 0; i < la; ++i) d[i] = a[i];
    for (int i = la - lb; i >= 0; --i) 
        while (greater_eq(d, b, i, lb)) 
            for (int j = 0; j < lb; ++j) 
                d[i + j] -= b[j];
                if (d[i + j] < 0) 
                    d[i + j + 1] -= 1;
                    d[i + j] += 10;
                
            
            c[i] += 1;

数论基础

平凡约数（平凡因数）：对于整数 \$b\\ne0\$，\$\\pm1\$、\$\\pm b\$ 是 \$b\$ 的平凡约数。当 \$b=\\pm1\$ 时，\$b\$ 只有两个平凡约数

对于整数 \$b\\ne 0\$，\$b\$ 的其他约数称为真约数（真因数、非平凡约数、非平凡因数）

同余

自反性：\$a\\equiv a\\pmod m\$
对称性：若 \$a\\equiv b\\pmod m\$，则 \$b\\equiv a\\pmod m\$
传递性：若 \$a\\equiv b\\pmod m\$,\$b\\equiv c\\pmod m\$，则 \$a\\equiv c\\pmod m\$
线性运算：若 \$a,b,c,d\\in\\mathbfZ\$,\$m\\in\\mathbfN^*\$,\$a\\equiv b\\pmod m\$,\$c\\equiv d\\pmod m\$ 则有：
- \$a\\pm c\\equiv b\\pm d\\pmod m\$
- \$a\\times c\\equiv b\\times d\\pmod m\$
若 \$a,b\\in\\mathbfZ,k,m\\in\\mathbfN^*\$,\$a\\equiv b\\pmod m\$, 则 \$ak\\equiv bk\\pmodmk\$
若 \$a,b\\in\\mathbfZ,d,m\\in\\mathbfN^*,d\\mid a,d\\mid b,d\\mid m\$，则当 \$a\\equiv b\\pmod m\$ 成立时，有\$\\dfracad\\equiv\\dfracbd\\left(\\bmod\\;\\dfracmd\\right)\$
若 \$a,b\\in\\mathbfZ,d,m\\in\\mathbfN^*,d\\mid m，则当 a\\equiv b\\pmod m 成立时，有 a\\equiv b\\pmod d\$
若 \$a,b\\in\\mathbfZ,d,m\\in\\mathbfN^*\$，则当 \$a\\equiv b\\pmod m\$ 成立时，有 \$\\gcd(a,m)=\\gcd(b,m)\$ 若 d 能整除 m 及 a,b 中的一个，则 d 必定能整除 a,b 中的另一个

素数

素数个数：\$\\pi(x) \\sim \\dfracx\\ln(x)\$

所有大于 3 的素数都可以表示为 \$6n\\pm 1\$ 的形式

int 范围内的素数间隔是小于 319 ， long long 范围内的素数间隔小于 1525

哥德巴赫猜想

关于偶数的哥德巴赫猜想：任一大于2的偶数都可写成两个素数之和。
关于奇数的哥德巴赫猜想：任一大于7的奇数都可写成三个质数之和的猜想。

`Miller_Rabin`

概率性素性测试

\$O(k \\log^3n)\$ \$k\$为测试次数

质因数分解

唯一分解定理

\$a=p_1^\\alpha_1p_2^\\alpha_2\\cdotsp_s^\\alpha_s,p_1<p_2<\\cdots<p_s\$

a 的正约数个数为 \$\\prod^s_i=1(c_i+1)\$

a 的所有正约数和为 \$\\prod^s_i=1(\\sum^c_i_j=0p^j_i)\$

n 的正因数个数上界是 \$2\\sqrt n\$

但实际上这个边界很宽松， \$10^9\$ 内的数，正因数最多有 1344 个；\$10^18\$ 内的数，正因数最多有 103680 个。

\$O(\\sqrt n)\$

void divide(int n)
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
            pri[++cnt]=i;
            c[cnt]=0;
            while(n%i==0)
                n/=i;
                c[cnt]++;
            
        
    
    if(n>1)
        pri[++cnt]=n;
        c[cnt]=1;

Pollard Rho 算法

Pollard-Rho 算法是一种用于快速分解非平凡因数的算法（注意！非平凡因子不是素因子）

\$O(n^\\frac14)\$ 通过倍增可以优化求 \$gcd\$ 的用时

P4718

对于每个数字检验是否是质数，是质数就输出 Prime；如果不是质数，输出它最大的质因子是哪个。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll gcd(ll a,ll b)
    return b?gcd(b,a%b):a;

inline ll qmul(ll a,ll b,ll P)//不用int128非常耗时
    return (__int128)a*b%P;
//    ll res=0;
//    while(b)
//        if(b&1) res=(res+a)%P;
//        a=(a+a)%P;
//        b>>=1;
//    
//    return res;

inline ll qpow(ll a,ll b,ll P)
    ll res=1;
    while(b)
        if(b&1) res=qmul(res,a,P);
        a=qmul(a,a,P);
        b>>=1;
    
    return res;

ll RandInt(ll l , ll r) //随机数
    static mt19937 Rand(time(0));
    uniform_int_distribution<ll> dis(l, r);
    return dis(Rand);

bool Miller_Rabin(ll n) 
    if(n < 3 || n % 2 == 0) return n == 2;
    ll a = n - 1 , b = 0;
    while(a % 2 == 0) 
        a /= 2;
        b++;
    
    for(int i = 1 , j; i <= 10; i++) 
        ll x = RandInt(2 , n - 1);
        ll v = qpow(x , a , n);
        if(v == 1) continue;
        for(j = 0; j < b; j++) 
            if(v == n - 1) break;
            v = qmul(v,v,n);
        
        if(j == b) return 0;
    
    return 1;

ll Pollard_Rho(ll n) 
    if(Miller_Rabin(n)||n==1) return n;//特判,n为1或极大质数是都会卡
    ll s = 0 , t = 0;
    ll c = RandInt(1 , n - 1);
    int step = 0 , goal = 1;
    ll value = 1;
    auto f = [=](ll x) 
        return (qmul(x,x,n)+c)%n;
    ;
    for(goal = 1;; goal <<= 1, s = t , value = 1) 
        for(step = 1; step <= goal; step++) 
            t = f(t);
            value = qmul(value , abs(t - s) , n);
            if(step % 127 == 0) 
                ll d = gcd(value , n);
                if(d > 1) return d;
            
        
        ll d = gcd(value , n);
        if(d > 1) return d;
    

ll Ans;
void Fac(ll n) //找最大质因子
    if(n <= Ans || n < 2) return;
    if(Miller_Rabin(n)) 
        Ans = max(Ans , n);
        return;
    
    ll p = n;
    while(p == n) p = Pollard_Rho(n);
    while((n % p) == 0) n /= p;
    Fac(n);
    Fac(p);

ll N,T;
int main() 
    cin >> T;
    while(T--) 
        Ans = 0;
        cin >> N;
        Fac(N);
        if(Ans == N) cout << "Prime" << endl;//最大质因子为自己则为质数
        else cout << Ans << endl;

质因数分解

queue<ll> aria;
void find(ll n) 
    if(n == 1) return;
    if(Miller_Rabin(n)) 
        aria.push(n);
        return;
    
    ll p = n;
    while(p == n) p = Pollard_Rho(n);
    find(p);
    find(n/p);

int main() 
    ll n;
    while(~scanf("%lld", &n)) 
        find(n);
        cout << aria.front();
        aria.pop();
        while(!aria.empty()) 
            cout << "*" << aria.front();
            aria.pop();
        
        cout << endl;
    
    return 0;

反素数

反素数：任何小于 n 的正数的约数个数都小于 n 的约数个数，即 n 以内因子最多且最小的数。

const int N=1e6+5,inf=0x3f3f3f3f;
int a[11]=0,2,3,5,7,11,13,17,19,23,29;//打表大法好（质因子种数不超过10）
long long n,ans,tot;//tot为求到的最大的约数个数
void f(long long x,long long now,long long shu,long long num)

    //x为当前递归的质因子，now为当前求得的数，num为now的约数个数 
    if(x==11)return ;//递归边界1
    long long tmp=1,i;
    for(i=1;i<=shu;i++)//当前递归的质因子的个数不超过shu（想不到其他变量名惹...无奈词汇量太小） 
    
        tmp*=a[x];//tmp暂时存储 
        if(now*tmp>n)return ;//递归边界2 
        if(num*(i+1)==tot&&now*tmp<ans)ans=now*tmp;//如果约数个数相同，并且当前得到的数now小于之前得到的数ans，那就更新ans；
        if(num*(i+1)>tot)//如果now的约数个数num大于之前求到的最大的约数个数tot，那就更新tot，并且更新ans；
        
            tot=num*(i+1);
            ans=now*tmp;
        
        f(x+1,now*tmp,i,num*(i+1));//往下递归

模型

求具有给定除数的最小自然数。请确保答案不超过 \$10^18\$

unsigned long long p[16] = 
    2,  3,  5,  7,  11, 13, 17, 19,
    23, 29, 31, 37, 41, 43, 47, 53;  // 根据数据范围可以确定使用的素数最大为53
unsigned long long ans;
unsigned long long n;
// depth: 当前在枚举第几个素数
// temp: 当前因子数量为 num的时候的数值
// num: 当前因子数
// up：上一个素数的幂，这次应该小于等于这个幂次嘛
void dfs(unsigned long long depth, unsigned long long temp,
         unsigned long long num, unsigned long long up) 
    if (num > n || depth >= 16) return;  // 边界条件
    if (num == n && ans > temp)         // 取最小的ans
        ans = temp;
        return;
    
    for (int i = 1; i <= up; i++) 
        if (temp * p[depth] > ans)
        break;  // 剪枝：如果加一个这个乘数的结果比ans要大，则必不是最佳方案
        dfs(depth + 1, temp = temp * p[depth], num * (i + 1),
        i);  // 取一个该乘数，进行对下一个乘数的搜索
    

int main() 
    scanf("%llu", &n);
    ans = ~(unsigned long long)0;
    dfs(0, 1, 1, 64);
    printf("%llu\\n", ans);
    return 0;

约数

\$O(\\log n)\$

ll gcd(ll a,ll b)
    return b?gcd(b,a%b);

ll lcm(ll a,ll b)
    return a/gcd(a,b)*b;

正因数集合的求法

试除法适用于求单个正整数 n 的正因数集合。

\$O(\\sqrt n)\$

void get_factor(int n, vector<int> &factor) 
    for (int i = 1;i * i <= n;i++) 
        if (!(n % i)) 
            factor.push_back(i);
            if (i != n / i) factor.push_back(n / i);

倍数法适用于求一个区间 \$[1,n]\$ 的每个数的正因数集合

此法常用于一些因子相关的求和，如\$\\sum^n_i=1\\sum_d\\mid i d\$

\$O(n\\log n)\$

const int N = 1e6 + 7;
vector<int> factor[N];
void get_factor(int n) 
    for (int i = 1;i <= n;i++)
        for (int j = 1;i * j <= n;j++)
            factor[i * j].push_back(i);

拓展欧几里得

常用于求 \$ax+by=\\gcd(a,b)\$ 的一组可行解

或求解 \$ax+by=m\$ 的解，当 \$m|\\gcd(a,b)\$ 时原方程有整数解为上式的解乘 \$\\fracm\\gcd(a,b)\$

对于模线性方程 \$ax≡b (mod n)\$ 可以化简为 \$ax + ny = b\$，设 \$d = gcd(a, n)\$ 当且仅当 \$b % d == 0\$ 时有解，且有d个解

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll exgcd(ll a,ll b,ll &x,ll &y)
    if(!b)x=1,y=0;return a;
    ll d=exgcd(b,a%b,x,y);
    ll t=x;x=y,y=t-(a/b)*y;
    return d;

ll a,b,c,x,y;
signed main()
    cin>>a>>b>>c;
    ll d=exgcd(a,b,x,y);
    cout<<d<<endl;
    if(c%d==0)
        x*=c/d,y*=c/d;//得到特解
        cout<<x<<" "<<y<<endl;
        ll p=b/d,q=a/d,k;
        if(x<0) k=ceil((1.0-x)/p),x+=p*k,y-=q*k;//x提到最小正整数
        else k=(x-1)/p,x-=p*k,y+=q*k;//x降到最小正整数
        if(y>0)//有在整数解组
            (y-1)/q+1;//解个数
            x+(y-1)/q*p;//最大正整x
            x;//最小正整x
            y;//最大正整y
            (y-1)%q+1;//最小正整y
        else
            x;//最小正整x
            y+q*(ll)ceil((1.0-y)/q);//最小正整y

由特解求通解

\$x\'=x_0+k*\\fracb\\gcd(a,b)\$

\$y\'=y_0-k*\\fraca\\gcd(a,b)\$

数论分块

一般 \$O(\\sqrt n)\$

一些小结论：

\$\\forall a,b,c\\in\\mathbbZ,\\left\\lfloor\\fracabc\\right\\rfloor=\\left\\lfloor\\frac\\left\\lfloor\\fracab\\right\\rfloorc\\right\\rfloor\$
对于常数 n，使得式子

\$\\left\\lfloor\\dfrac ni\\right\\rfloor=\\left\\lfloor\\dfrac nj\\right\\rfloor\$

成立的最大的满足 \$i\\leq j\\leq n\$ 的 j 的值为 \$\\left\\lfloor\\dfrac n\\lfloor\\frac ni\\rfloor\\right\\rfloor\$。即值 \$\\left\\lfloor\\dfrac ni\\right\\rfloor\$ 所在的块的右端点为 \$\\left\\lfloor\\dfrac n\\lfloor\\frac ni\\rfloor\\right\\rfloor\$
\$a\\%b\$ 可以表示为 \$a-b*\\lfloor\\fracab\\rfloor\$ 此结论可用于高精度取模

数论分块的过程大概如下：考虑和式

\\[\\sum_i=1^nf(i)\\left\\lfloor\\dfrac ni\\right\\rfloor \\]

那么由于我们可以知道

\$\\left\\lfloor\\dfrac ni\\right\\rfloor\$ 的值成一个块状分布（就是同样的值都聚集在连续的块中），那么就可以用数论分块加速计算，降低时间复杂度。

利用上述结论，我们先求出 \$f(i)\$ 的前缀和（记作 \$s(i)=\\sum_j=1^i f(j)\$），然后每次以 \$[l,r]=[l,\\left\\lfloor\\dfrac n\\lfloor\\frac ni\\rfloor\\right\\rfloor]\$ 为一块，分块求出贡献累加到结果中即可。

N 维数论分块

求含有 \$\\left\\lfloor\\dfrac a_1i\\right\\rfloor\$、\$\\left\\lfloor\\dfrac a_2i\\right\\rfloor\\cdots\\left\\lfloor\\dfrac a_ni\\right\\rfloor\$ 的和式时，数论分块右端点的表达式从一维的 \$\\left\\lfloor\\dfrac ni\\right\\rfloor\$ 变为 \$\\min\\limits_j=1^n\\\\left\\lfloor\\dfrac a_ji\\right\\rfloor\\\$，即对于每一个块的右端点取最小（最接近左端点）的那个作为整体的右端点。可以借助下图理解：

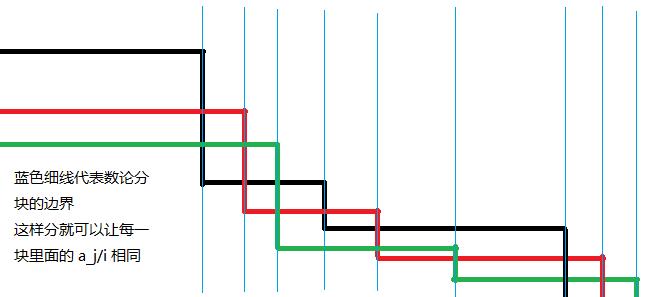
一般我们用的较多的是二维形式，此时可将代码中 r = n / (n / i) 替换成 r = min(n / (n / i), m / (m / i))

大数阶乘取模

似乎不太算数论分块QAQ\$(1 \\le N \\le 1e10)\$

分块打表,每1e7个数打一个表

const int a[100]=
682498929,491101308,76479948,723816384,67347853,27368307,625544428,199888908,888050723,927880474,
281863274,661224977,623534362,970055531,261384175,195888993,66404266,547665832,109838563,933245637,724691727,
368925948,268838846,136026497,112390913,135498044,217544623,419363534,500780548,668123525,128487469,30977140,
522049725,309058615,386027524,189239124,148528617,940567523,917084264,429277690,996164327,358655417,568392357,
780072518,462639908,275105629,909210595,99199382,703397904,733333339,97830135,608823837,256141983,141827977,
696628828,637939935,811575797,848924691,131772368,724464507,272814771,326159309,456152084,903466878,92255682,
769795511,373745190,606241871,825871994,957939114,435887178,852304035,663307737,375297772,217598709,624148346,
671734977,624500515,748510389,203191898,423951674,629786193,672850561,814362881,823845496,116667533,256473217,
627655552,245795606,586445753,172114298,193781724,778983779,83868974,315103615,965785236,492741665,377329025,
847549272,698611116
;//。。。
const int MOD=1000000007;
int main()
    cin>>n>>p;
    if (p==1000000007)
        if (n>=p) 
            cout<<"0";
            return 0;
        
        if(n<10000000) now=1;
        else now=a[n/10000000-1];
        for(int i=n/10000000*10000000+1;i<=n;i++) now=now*i%MOD;
     else
        now=1;
        if (n>=p) now=0; 
        else for(int i=1;i<=n;i++) 
                now=now*i%p;
    
    cout<<now<<endl;

P2261[CQOI2007]余数求和

给出正整数 \$n\$ 和 \$k\$，请计算

\\[G(n, k) = \\sum_i = 1^n k \\bmod i \\]

\$ans=\\sum^n_i=1 k-i*\\lfloor\\fracki\\rfloor=n*k-\\sum^n_i=1i*\\lfloor\\fracki\\rfloor\$

ll ans=n*k;
for(ll l=1,r;l<=n;l=r+1) 
    if(k/l!=0) r=min(k/(k/l),n); 
    else r=n;
    ans-=(k/l)*(r-l+1)*(l+r)/2;

Calculating

若 \$x\$ 分解质因数结果为 \$x=p_1^k_1p_2^k_2\\cdots p_n^k_n\$，令\$f(x)=(k_1+1)(k_2+1)\\cdots (k_n+1)\$，求 \$\\sum_i=l^rf(i)\$ 对 \$998\\,244\\,353\$ 取模的结果。

明显 \$f(i)\$ 表示的是i的因子个数

则有：\$\\sum^n_i=1f(i)=\\sum^n_i=1\\lfloor\\fracni\\rfloor\$

略证：设 \$i\$ 为因子, 有 \$n/i\$ 个数含有因子 \$i\$

int block(int n)
    int res=0;
    for(int l=1,r;l<=n;l=r+1)
        r=n/(n/l);
        res=(res+(n/l)*(r-l+1)%P)%P;
    
    return res;

void solve()
    cout<<(block(r)-block(l-1)+P)%P<<endl;

欧拉函数

欧拉函数（Euler\'s totient function），即 \$\\varphi(n)\$，表示的是小于等于 \$n\$ 和 \$n\$ 互质的数的个数

\\[\\varphi(n)=\\sum_i=1^n[(i,n)=1] \\]

比如说 \$\\varphi(1) = 1\$

当 \$n\$ 是质数的时候，显然有 \$\\varphi(n) = n - 1\$

性质:

欧拉函数是积性函数。

即如果有 \$\\gcd(a, b) = 1\$，那么 \$\\varphi(a \\times b) = \\varphi(a) \\times \\varphi(b)\$

特别地，当 \$n\$ 是奇数时 \$\\varphi(2n) = \\varphi(n)\$
\$n = \\sum_d \\mid n\\varphi(d)\$
若 \$n = p^k\$，其中 \$p\$ 是质数，那么 \$\\varphi(n) = p^k - p^k - 1\$
由唯一分解定理，设 \$n = \\prod_i=1^sp_i^k_i\$，其中 \$p_i\$ 是质数，有 \$\\varphi(n) = n \\times \\prod_i = 1^s\\dfracp_i - 1p_i\$

求单个数的欧拉函数,直接根据定义质因数分解的同时求就好了,可以用Pollard Rho优化

int euler_phi(int n) 
    int ans = n;
    for (int i = 2; i * i <= n; i++)
    if (n % i == 0) 
        ans = ans / i * (i - 1);
        while (n % i == 0) n /= i;
    
    if (n > 1) ans = ans / n * (n - 1);
    return ans;

欧拉定理

\$\\gcd(a, m) = 1\$，则 \$a^\\varphi(m) \\equiv 1 \\pmodm\$

扩展欧拉定理

\\[a^b\\equiv \\begincases a^b\\bmod\\varphi(p), &\\gcd(a,\\,p)=1\\\\ a^b,&\\gcd(a,\\,p)\\ne1,\\,b<\\varphi(p)\\\\ a^b\\bmod\\varphi(p)+\\varphi(p),&\\gcd(a,\\,p)\\ne1,\\,b\\ge\\varphi(p) \\endcases \\pmod p \\]

裴蜀定理

设 \$a\$,\$b\$ 是不全为零的整数，则存在整数 \$x\$,\$y\$, 使得 \$ax+by=\\gcd(a,b)\$

推论

设自然数 a、b 和整数 n。a 与 b 互素。考察不定方程：\$ax+by=n\$ 其中 x 和 y 为自然数。如果方程有解，称 n 可以被 a、b 表示。

记 \$C=ab-a-b\$。由 a 与 b 互素，C 必然为奇数。则有结论：

对任意的整数 n，n 与 C-n 中有且仅有一个可以被表示。

即：可表示的数与不可表示的数在区间 [0,C] 对称（关于 C 的一半对称）。0 可被表示，C 不可被表示；负数不可被表示，大于 C 的数可被表示。

noip2017

小凯手中有两种面值的金币，两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下，仅凭这两种金币，有些物品他是无法准确支付的。现在小凯想知道在无法准确支付的物品中，最贵的价值是多少金币？

ans=ab-a-b

NOIP2005 过河

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0，1，……，L（其中L是桥的长度）。坐标为0的点表示桥的起点，坐标为L的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数（包括S,T）。当青蛙跳到或跳过坐标为L的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度L（1<=L<=1e9），青蛙跳跃的距离范围S,T<=10，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

路径压缩

假设每次走p或者p+1步.我们知道 \$\\gcd(p,p+1)=1\$

我们需要求得一个最小的值tt使得对于所有\$s>t\$ 的 \$px+(p+1)y=spx+(p+1)y=s\$一定有非负整数解。根据NOIP2017提高组D1T1的结论，我们可以知道这个数为 \$t=p(p+1)-p-(p+1)t=p(p+1)−p−(p+1)\$。由于本题的最大步长为10，因此 \$t_max=9\\times10-9-10=71\$

但是要注意，对于 \$s=t\$ 这种特殊情况，这种方法是不成立的应为在这种情况下，每次是不能够走p+1步的，因此需要另外特殊判断。

而且有可能跳过终点,所以dp的时候要循环到L+t-1

a,b不互质时不便压缩,因为必须有 \$s|\\gcd(a,b)\$

欧拉定理 & 费马小定理

费马小定理:

若 \$p\$ 为素数，\$\\gcd(a, p) = 1\$，则 \$a^p - 1 \\equiv 1 \\pmodp\$

欧拉定理:

若 \$\\gcd(a, m) = 1\$，则 \$a^\\varphi(m) \\equiv 1 \\pmodm\$

扩展欧拉定理:

无论是费马小定理，还是（扩展）欧拉定理，一个很重要的应用就是降幂，从而将不可能的表达式化为可能

cf Notepad

你有一个本子，你要往上面写全部的长度为\$n\$的\$b\$进制数字，每一页可以写\$c\$个。要求所有数字必须严格不含前导\$0\$。求最后一页上有多少个数字

\$2~\\leq~b~<~10^10^6~,~1~\\leq~n~<~10^10^6~,~1~\\leq~c~\\leq~10^9\$

即求 \$(a-1)a^n-1 mod p\$

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1000010;
char sa[N],sn[N];
ll p,a,n,phi,q,ans;
int len1,len2;
bool flag;
ll power(ll x,ll k)
    ll ans=1;
    for (;k;k>>=1,x=x*x%p)
        if (k&1) ans=ans*x%p;
    return ans;

int main()
    scanf("%s %s %lld",sa+1,sn+1,&p);
    phi=q=p; len1=strlen(sa+1); len2=strlen(sn+1);
    for (ll i=2;i*i<=q;i++)if (!(q%i))
            phi=phi/i*(i-1);
            while (!(q%i)) q/=i;
        
    if (q>1) phi=phi/q*(q-1);
    for (int i=1;i<=len1;i++)
        a=(a*10+sa[i]-48)%p;
    for (int i=len2;i>=1;i--)  //n-1
        if (sn[i]==48) sn[i]=\'9\';
        else
            sn[i]--;
            break;
        
    for (int i=1;i<=len2;i++)
        n=n*10+sn[i]-48;
        if (n>=phi) flag=1;
        n%=phi;
    
    if (flag) n+=phi;
    ans=((a-1)*power(a,n)%p+p)%p;  //注意这里可能为负数，所以要加p再模p，被HACK了一次
    if (ans) printf("%lld",ans);
    else printf("%lld",p);
    return 0;

逆元

如果一个线性同余方程 \$ax \\equiv 1 \\pmod b\$，则 \$x\$ 称为 \$a \\bmod b\$ 的逆元，记作 \$a^-1\$

\$b\$ 为素数时 \$x=a^b-2\$

a,b不互质时,有公式: \$x/d \\% m = x\\%(d*m)/d\$

线性求逆元

inv[0] = 0;
inv[1] = 1;
for (int i = 2; i <= n; ++i) 
  inv[i] = (ll)(p - p / i) * inv[p % i] % p;

线性求任意\$n\$个数的逆元

首先计算 \$n\$ 个数的前缀积，记为 \$s_i\$，然后使用快速幂或扩展欧几里得法计算 \$s_n\$ 的逆元，记为 \$sv_n\$。

因为 \$sv_n\$ 是 \$n\$ 个数的积的逆元，所以当我们把它乘上 \$a_n\$ 时，就会和 \$a_n\$ 的逆元抵消，于是就得到了 \$a_1\$ 到 \$a_n-1\$ 的积逆元，记为 \$sv_n-1\$

同理我们可以依次计算出所有的 \$sv_i\$，于是 \$a_i^-1\$ 就可以用 \$s_i-1 \\times sv_i\$ 求得。

s[0] = 1;
for (int i = 1; i <= n; ++i) s[i] = s[i - 1] * a[i] % p;//
sv[n] = qpow(s[n], p - 2);
for (int i = n; i >= 1; --i) sv[i - 1] = sv[i] * a[i] % p;
for (int i = 1; i <= n; ++i) inv[i] = sv[i] * s[i - 1] % p;

求整数除法小数点后的第n位开始的3位数（0<a,b,n<1000000000）

即求 \$a*10^n+2\\%(b*1000)/b\$

线性同余方程

\$ax\\equiv b\\pmod n\$

等价于: \$ax+nk=b\$

有整数解的充要条件为 \$\\gcd(a,n) \\mid b\$

中国剩余定理

中国剩余定理 (Chinese Remainder Theorem, CRT) 可求解如下形式的一元线性同余方程组（其中 \$n_1\$, \$n_2\$, \$\\cdots\$, \$n_k\$ 两两互质）：

\\[\\begincases x &\\equiv a_1 \\pmod n_1 \\\\ x &\\equiv a_2 \\pmod n_2 \\\\ &\\vdots \\\\ x &\\equiv a_k \\pmod n_k \\\\ \\endcases \\]

过程

计算所有模数的积 \$n\$
对于第 \$i\$ 个方程：
1. 计算 \$m_i=\\fracnn_i\$
2. 计算 \$m_i\$ 在模 \$n_i\$ 意义下的逆元 \$m_i^-1\$
3. 计算 \$c_i=m_im_i^-1\$（不要对 \$n_i\$ 取模）
方程组在模 \$n\$ 意义下的唯一解为：
\$x=\\sum_i=1^k a_ic_i \\pmod n\$

ll crt(int k, ll* a, ll* r) 
    ll n = 1, ans = 0;
    for (int i = 1; i <= k; i++) n = n * r[i];
    for (int i = 1; i <= k; i++) 
        ll m = n / r[i], b, y;
        exgcd(m, r[i], b, y);  // b * m mod r[i] = 1
        //r[i]为质数可以用费马，r[i]互质用exgcd
        ans = (ans + a[i] * m * b % n) % n;//可能被卡,用__int128
    
    return (ans % n + n) % n;

Garner 算法

\$O(k^2)\$

CRT 的另一个用途是用一组比较小的质数表示一个大的整数。

例如，若 \$a\$ 满足如下线性方程组，且 \$a < \\prod_i=1^k p_i\$（其中 \$p_i\$ 两两互质）：

\\[\\begincases a &\\equiv a_1 \\pmod p_1 \\\\ a &\\equiv a_2 \\pmod p_2 \\\\ &\\vdots \\\\ a &\\equiv a_k \\pmod p_k \\\\ \\endcases \\]

我们可以用以下形式的式子（称作 \$a\$ 的混合基数表示）表示 \$a\$ ：

\$a = x_1 + x_2 p_1 + x_3 p_1 p_2 + \\ldots + x_k p_1 \\ldots p_k-1\$

Garner算法将用来计算系数 \$x_1, \\ldots, x_k\$

令 \$r_ij\$ 为 \$p_i\$ 在模 \$p_j\$ 意义下的逆：\$p_i \\cdot r_i,j \\equiv 1 \\pmodp_j\$

for (int i = 0; i < k; ++i) 
    x[i] = a[i];
    for (int j = 0; j < i; ++j) 
        x[i] = r[j][i] * (x[i] - x[j]);
        x[i] = x[i] % p[i];
        if (x[i] < 0) x[i] += p[i];

扩展：模数不互质的情况

ll excrt(int k,ll a[],ll r[])
    ll n=r[1],ans=a[1];//第一个方程的解特判
    for(int i=2;i<=k;i++)
        ll b=r[i],c=(a[i]-ans%b+b)%b,x,y;//ax≡c(mod b)
        ll d=exgcd(n,b,x,y),bg=b/d;
        if(c%d!=0) return -1; //判断是否无解
        x=(lll)c/d*x%bg;
        ans+=x*n;//更新前k个方程组的答案
        n*=bg;//M为前k个m的lcm
        ans=(ans%n+n)%n;
    
    return (ans%n+n)%n;

P2480 古代猪文

给出 \$1 \\leq G,n \\leq 10^9\$ 求 \$G^\\sum_k\\mid n\\binomnk \\bmod 999911659\$

由欧拉定理转化为: \$G^\\sum_k\\mid n\\binomnk\\bmod 999911658 \\bmod 999911659\$

明显 \$999911658\$ 不是质数但可以分解为: \$2*3*4679*35617\$

构造出同余方程组:

\\[\\begincases x &\\equiv \\sum_k\\mid n\\binomnk \\pmod 2 \\\\ x &\\equiv \\sum_k\\mid n\\binomnk \\pmod 3 \\\\ x &\\equiv \\sum_k\\mid n\\binomnk \\pmod 4679 \\\\ x &\\equiv \\sum_k\\mid n\\binomnk \\pmod 35617 \\\\ \\endcases \\]

发现四个数都很小而且都是质数,可以用Lucas定理求出 \$a_i\$ 后用CRT求 \$x\$

#include <bits/stdc++.h>
using namespace std;
#define Mod 999911659
#define mod 999911658
#define maxn 40005
#define ll long long
ll n,g,d[maxn],tot,p[10],cnt;
inline ll qpow(ll a,ll k,ll p)
    ll res=1;
    while(k)
    
        if(k&1) res=(res*a)%p;
        a=(a*a)%p;
        k>>=1;
    
    return res%p;

ll fac[maxn],inv[maxn];
inline void init(ll p)
    fac[0]=1;
    for(int i=1;i<p;i++) fac[i]=fac[i-1]*i%p;
    inv[p]=0;
    inv[p-1]=qpow(fac[p-1],p-2,p);
    for(int i=p-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%p;

inline ll C(ll n,ll m,ll p)
    if(m>n) return 0;
    return fac[n]*inv[m]%p*inv[n-m]%p;

inline ll Lucas(ll n,ll m,ll p)
    if(m==0) return 1;
    return Lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;

ll a[10];
inline void calc(int x)
    init(p[x]);
    for(int i=1;i<=tot;i++)
        a[x]=(a[x]+Lucas(n,d[i],p[x]))%p[x];

inline ll CRT()
    ll ans=0;
    for(int i=1;i<=cnt;i++)
        ll M=mod/p[i],t=qpow(M,p[i]-2,p[i]);
        ans=(ans+a[i]%mod*t%mod*M%mod)%mod;
    
    return (ans+mod)%mod;

int main()
    scanf("%lld%lld",&n,&g);
    if(g%Mod==0)
        printf("0\\n");
        return 0;
    
    ll t=mod;
    for(int i=2;i*i<=mod;i++)
        if(t%i==0)
            p[++cnt]=i;
            while(t%i==0) t=t/i;
        
    
    if(t!=1) p[++cnt]=t;
    for(int i=1;i*i<=n;i++)
        if(n%i==0)
            d[++tot]=i;
            if(i*i!=n) d[++tot]=n/i;
        
    
    for(int i=1;i<=cnt;i++) calc(i);
    printf("%lld",qpow(g,CRT(),Mod));

威尔逊定理

Wilson 定理：对于素数 \$p\$ 有 \$(p-1)!\\equiv -1\\pmod p\$

hdu 6608

给出一个质数P，找出小于P的最大的质数N，求出N的阶乘模P。（P∈[1e10,1e14]）

一个数\$n\$若是质数，则有\$(n−1)!\\equiv n−1\\pmod n\$. 于是可以先令\$ans=p−1\$, 再对\$p−1\$到\$q\$的数对\$p\$求逆元。\$p\$到\$q\$之间的距离大约300以上，Miller Robin大素数判断可以找到最近的素数。

int main()
    cin>>t;
    while(t--)
        cin >> Q;
        ll ans;
        for(ll i=Q-1;;i--)
            if(Miller_Rabin(i))
                ans=i;
                break;
            
        
        ll sum=Q-1;
        for(ll i=ans+1;i<Q;i++)
            sum=mult_mod(sum,pow_mod(i,Q-2,Q),Q);
        
        cout<<sum<<endl;

卢卡斯定理

\$\\binomnm\\bmod p = \\binom\\left\\lfloor n/p \\right\\rfloor\\left\\lfloor m/p\\right\\rfloor\\cdot\\binomn\\bmod pm\\bmod p\\bmod p\$

要求 p 的范围不能够太大，一般在 10^5 左右。边界条件：当 m=0 的时候，返回 1。

时间复杂度为 \$O(f(p) + g(n)\\log n)\$，其中 \$f(n)\$ 为预处理组合数的复杂度，\$g(n)\$ 为单次求组合数的复杂度。

ll Lucas(ll n,ll m,ll p) 
  if (m == 0) return 1;
  return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;

exlucas
P4720

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll ksm(ll a,ll b,ll P)
    ll res=1;
    while(b)
        if(b&1) res=res*a%P;
        a=a*a%P;
        b>>=1;
    
    return res;

ll exgcd(ll a,ll b,ll &x,ll &y)
    if(!b)x=1,y=0;return a;
    ll d=exgcd(b,a%b,x,y);
    ll t=x;x=y,y=t-(a/b)*y;
    return d;

ll CRT(int n, ll* a, ll* m) 
    ll M = 1, p = 0;
    for (int i = 1; i <= n; i++) M = M * m[i];
    for (int i = 1; i <= n; i++) 
        ll w = M / m[i], x, y;
        exgcd(w, m[i], x, y);
        p = (p + a[i] * w * x % M) % M;
    
    return (p % M + M) % M;

ll calc(ll n, ll x, ll P) 
    if (!n) return 1;
    ll s = 1;
    for (ll i = 1; i <= P; i++)
        if (i % x) s = s * i % P;
    s = ksm(s, n / P, P);
    for (ll i = n / P * P + 1; i <= n; i++)
        if (i % x) s = i % P * s % P;
    return s * calc(n / x, x, P) % P;

ll inverse(ll a,ll P)//求逆元，因为P不一定为质数所以用exgcd，用费马会wa一个点
    ll x,y;
    exgcd(a,P,x,y);
    return x;

ll multilucas(ll m, ll n, ll x, ll P) 
    int cnt = 0;
    for (ll i = m; i; i /= x) cnt += i / x;
    for (ll i = n; i; i /= x) cnt -= i / x;
    for (ll i = m - n; i; i /= x) cnt -= i / x;
    return ksm(x, cnt, P) % P * calc(m, x, P) % P * inverse(calc(n, x, P), P) %
           P * inverse(calc(m - n, x, P), P) % P;

ll exlucas(ll m, ll n, ll P) 
    int cnt = 0;
    ll p[20], a[20];
    for (ll i = 2; i * i <= P; i++) 
        if (P % i == 0) 
            p[++cnt] = 1;
            while (P % i == 0) p[cnt] = p[cnt] * i, P /= i;
            a[cnt] = multilucas(m, n, i, p[cnt]);
        
    
    if (P > 1) p[++cnt] = P, a[cnt] = multilucas(m, n, P, P);
    return CRT(cnt, a, p);

int main()
    ll a,b,c;
    cin>>a>>b>>c;
    cout<<exlucas(a,b,c)<<\'\\n\';

二次剩余

一个数 \$a\$，如果不是 \$p\$ 的倍数且模 \$p\$ 同余于某个数的平方，则称 \$a\$ 为模 \$p\$ 的二次剩余。而一个不是 \$p\$ 的倍数的数 \$b\$，不同余于任何数的平方，则称 \$b\$ 为模 \$p\$ 的二次非剩余。

对二次剩余求解，也就是对常数 \$a\$ 解下面的这个方程：

\\[x^2 \\equiv a \\pmod p \\]

通俗一些，可以认为是求模意义下的开平方运算。

这里只讨论 \$\\boldsymbolp\$ 为奇素数的求解方法

对于奇素数 \$p\$ 和集合 \$\\left\\lbrace 1,2,\\dots ,p-1\\right\\rbrace\$，在模 \$p\$ 意义下二次剩余的数量等于二次非剩余的数量,即 \$\\fracp-12\$

欧拉准则

\$n^\\fracp-12 \\equiv 1\$与 \$n\$ 是二次剩余是等价的，由于 \$n^\\fracp-12\$ 不为 \$1\$ 是只能是 \$-1\$ ，那么 \$n^\\fracp-12 \\equiv -1\$与 \$n\$ 是非二次剩余等价。

Cipolla

给出 \$N,p\$，求解方程:

\\[x^2 \\equiv N \\pmodp \\]

多组数据，且保证 \$p\$ 是奇素数。

输出共 \$T\$ 行。

对于每一行输出，若有解，则按 \$\\bmod ~p\$ 后递增的顺序输出在 \$\\bmod~ p\$ 意义下的全部解；若两解相同，只输出其中一个；若无解，则输出Hola!

#include<bits/stdc++.h>
using namespace std;
#define ll long long
struct num 
    ll x;// 实部
    ll y;// 虚部(即虚数单位√w的系数)
;
ll t,w,n,p;
num mul(num a,num b,ll p) // 复数乘法
    num res;
    res.x=( (a.x*b.x%p+a.y*b.y%p*w%p) %p+p)%p;// x = a.x*b.x + a.y*b.y*w
    res.y=( (a.x*b.y%p+a.y*b.x%p) %p+p)%p;// y = a.x*b.y + a.y*b.x
    return res;

ll qpow_r(ll a,ll b,ll p) // 实数快速幂
    ll res=1;
    while(b) 
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    
    return res;

ll qpow_i(num a,ll b,ll p) // 复数快速幂
    num res=1,0;
    while(b) 
        if(b&1) res=mul(res,a,p);
        a=mul(a,a,p);
        b>>=1;
    
    return res.x%p;// 只用返回实数部分，因为虚数部分没了

ll cipolla(ll n,ll p) 
    n%=p;
    if(qpow_r(n,(p-1)/2,p)==-1+p) return -1;// 据欧拉准则判定是否有解
    ll a;
    while(1) // 找出一个符合条件的a
        a=rand()%p;
        w=( ((a*a)%p-n) %p+p)%p;// w = a^2 - n，虚数单位的平方
        if(qpow_r(w,(p-1)/2,p)==-1+p) break;
    
    num x=a,1;
    return qpow_i(x,(p+1)/2,p);

int main() 
    srand(time(0));
    cin>>t;
    while(t--) 
        cin>>n>>p;
        if(!n) 
            printf("0\\n");
            continue;
        
        ll ans1=cipolla(n,p),ans2=-ans1+p;// 另一个解就是其相反数
        if(ans1==-1) printf("Hola!\\n");
        else 
            if(ans1>ans2) swap(ans1,ans2);
            if(ans1==ans2) printf("%lld\\n",ans1);
            else printf("%lld %lld\\n",ans1,ans2);

Dirichlet 卷积

参考链接:

https://blog.bill.moe/multiplicative-function-sieves-notes/

对于两个数论函数 f(x) 和 g(x)，则它们的狄利克雷卷积得到的结果 h(x) 定义为：

\\[h(x)=\\sum_d\\mid xf(d)g\\left(\\dfrac xd \\right)=\\sum_ab=xf(a)g(b) \\]

上式可以简记为：

\\[h=f*g \\]

满足交换律，结合律，分配律

数论函数的积性，在狄利克雷生成函数中的对应具有封闭性

等式的性质: \$f=g\$ 的充要条件是 \$f*h=g*h\$，其中数论函数 \$h(x)\$ 要满足 \$h(1)\\ne 0\$

数论函数

定义域为正整数的函数，值域为复数的函数。

积性函数

规定 \$f(1)=1\$，当 \$(a,b)=1\$ 时满足 \$f(ab)=f(a)f(b)\$ 的函数

特别地: 满足 \$∀a,b，f(ab)=f(a)f(b)\$ ,则为完全积性函数

常见的积性函数:

\\[\\varepsilon(n)=[n=1](完全积性)\\\\ id(n)=n,id_k(n)=n^k(完全积性)\\\\ 1(n)=1(完全积性)\\\\ d(n)=\\sum_i\\mid n 1\\\\ \\sigma(n)=\\sum_i\\mid ni\\\\ \\sigma_k(n)=\\sum_i\\mid ni^k\\\\ \\mu(n)= \\begincases 1&n=1\\\\ 0&n\\text 含有平方因子\\\\ (-1)^k&k\\text 为 n\\text 的本质不同质因子个数\\\\ \\endcases\\\\ \\varphi(n)=\\sum_i=1^n[(i,n)=1]\\\\ \\]

单位元

单位函数 \$\\varepsilon\$ 是 Dirichlet 卷积运算中的单位元，即对于任何数论函数 \$f\$，都有 \$f*\\varepsilon=f\$

\\[\\varepsilon(x)=[x=1] \\]

逆元：

对于任何一个满足 \$f(x)\\ne 0\$ 的数论函数，如果有另一个数论函数 \$g(x)\$ 满足 \$f*g=\\varepsilon\$，则称 \$g(x)\$ 是 \$f(x)\$ 的逆元。由等式的性质可知，逆元是唯一的

常见的卷积

注意:转化是等号两侧的转化,双向箭头两侧只是表达方式不同

\\[d(n)=\\sum_d\\mid n1\\quad\\Leftrightarrow\\quad d=1*1\\\\ \\sigma(n)=\\sum_d\\mid nd\\quad\\Leftrightarrow\\quad \\sigma=d*1\\\\ \\varphi(n)=\\sum_d\\mid n\\mu(d)\\frac nd\\quad\\Leftrightarrow\\quad\\varphi=\\mu*id\\\\ e(n)=\\sum_d\\mid n\\mu(d)\\quad\\Leftrightarrow\\quad e=\\mu*1\\\\ \\]

线性筛

要求

\$f(x)\$ 为积性函数

线性筛思想

\\[n=\\prod_i=1^kp_i^a_i \\]

使用最小的 \$p_1\$ 去筛掉其他的数。

将 \$n\$ 分为三类考虑

\$n\$ 是质数,根据定义得到\$f(i)\$的值
\$\\frac np_1\\bmod p_1=0\$,说明\$\\fracnp_1\$与\$n\$的质因子集相同，考虑其变化。
\$\\frac np_1\\bmod p_1\\neq0\$,说明\$\\fracnp_1\$与\$p_1\$互质,利用积性函数的性质得到\$f(n)=f(\\frac np_1)f(p_1)\$

素数线性筛

int vst[maxn],Prime[maxn],cnt=0; //prime

void Prime_Sieve(int n) 
    for(int i=2; i<=n; i++) 
        if(!vst[i])Prime[++cnt]=i;
        for(int j=1; j<=cnt&&i*Prime[j]<=n; j++) 
            vst[i*Prime[j]]=1;
            if(i%Prime[j]==0)break;

欧拉函数

设\$p_1\$是\$n\$的最小质因子，\$n\'=\\fracnp_1\$，在线性筛中，\$n\$通过\$n\'\\times p1\$被筛掉。

当\$n\'\\bmod p_1=0\$,即\$a_1 \\gt 1\$时,\$n\'\$含有\$n\$的所有质因子，则有：
\\[\\varphi(n)=p_1 \\times \\varphi(n\') \\]
当\$n\'\\bmod p_1\\neq 0\$即\$a_1=1\$时，\$n\'\$与\$p_1\$互素，而欧拉函数是积性函数，故：
\\[\\varphi(n)=(p_1-1) \\varphi(n\') \\]

const int maxn=1000005;

int vst[maxn],Prime[maxn],cnt=0; //prime
int Phi[maxn]; //phi

void Phi_Table(int n) 
    Phi[1]=1;
    for(int i=2; i<=n; i++) 
        if(!vst[i]) 
            Prime[++cnt]=i;
            Phi[i]=i-1;
        
        for(int j=1; j<=cnt&&i*Prime[j]<=n; j++) 
            vst[i*Prime[j]]=1;
            if(i%Prime[j]==0) 
                Phi[i*Prime[j]]=Phi[i]*Prime[j];
                break;
            
            Phi[i*Prime[j]]=Phi[i]*Phi[Prime[j]];

莫比乌斯函数

https://www.cnblogs.com/icyM3tra/p/16150523.html

当\$n\$为素数时,根据定义有\$\\mu(n)=-1\$

设\$p_1\$是\$n\$的最小质因子，\$n\'=\\fracnp_1\$，在线性筛中，\$n\$通过\$n\'\\times p1\$被筛掉。

当\$n\'\\bmod p_1=0\$,即\$a_1 \\gt 1\$时,由定义可知：
\\[\\mu(n)=0 \\]
当\$n\'\\bmod p_1\\neq 0\$即\$a_1=1\$时，\$n\'\$与\$p_1\$互素，而莫比乌斯函数是积性函数，故：
\\[\\mu(n)=- \\mu(n\') \\]

const int maxn=1000005;

int vst[maxn],Prime[maxn],cnt=0; //prime
int Mobius[maxn]; //mobius

void Mobius_Table(int n) 
    Mobius[1]=1;
    for(int i=2; i<=n; i++) 
        if(!vst[i]) 
            Prime[++cnt]=i;
            Mobius[i]=-1;
        
        for(int j=1; j<=cnt&&i*Prime[j]<=n; j++) 
            vst[i*Prime[j]]=1;
            if(i%Prime[j]==0) 
                Mobius[i*Prime[j]]=0;
                break;
            
            Mobius[i*Prime[j]]=-Mobius[i];

P4450 双亲数

求\$\\sum^A_i=1\\sum^B_j=1[(i,j)==d],1\\leq A,B \\leq 10^6\$

常用套路:\$[(i,j)==1]=\\sum_t|(i,j)\\mu(t)=\\sum_t|i,t|j\\mu(t)\$

\\[\\beginaligned \\sum^A_i=1\\sum^B_j=1[(i,j)==d]&=\\sum^A/d_i=1\\sum^B/d_j=1[(i,j)==1]\\\\ &=\\sum^A/d_i=1\\sum^B/d_j=1\\sum_t|(i,j)\\mu(t)\\\\ &=\\sum^\\min(A,B)/d_t=1\\mu(t)\\sum^A/d_i=1[t|i]\\sum^B/d_j=1[t|j]\\\\ &=\\sum^\\min(A,B)/d_t=1\\mu(t)(\\fracAdt)(\\fracBdt) \\endaligned \\]

P1829

求\$\\sum^A_i=1\\sum^B_j=1lcm(i,j),1\\leq n,m\\leq 10^7\$

\\[\\beginaligned \\sum_i=1^n\\sum_j=1^m\\rm lcm(i,j) &=\\sum_d=1^N\\sum_i=1^n\\sum_j=1^m[(i,j)=d]\\fracijd \\\\ &=\\sum_d=1^Nd\\sum_i=1^n/d\\sum_j=1^m/d[(i,j)=1]ij \\\\ &=\\sum_d=1^Nd\\sum_i=1^n/d\\sum_j=1^m/d\\sum_t|i,t|j\\mu(t)ij\\\\ &=\\sum_d=1^Nd\\sum_t=1^N/d\\mu(t)\\sum_i=1^n/d[t|i]i\\sum_j=1^m/d[t|j]j\\\\ &=\\sum_d=1^Nd\\sum_t=1^N/d\\mu(t)t^2S(\\fracndt)S(\\fracmdt) \\endaligned \\]

其中\$S(n)=\\fracn(n+1)2\$

欧拉反演

大部分莫反题都是用\$\\sum_d|n\\mu(d)代换式子中出现的\$[n=1]$

但在某些情形下，存在另一种做法：用\$\\sum_d|n\\varphi(d)\$代换式子里的\$n\$

P1447

求\$\\sum^n_i=1\\sum^m_j=12(i,j)-1,1\\leq n,m \\leq 10^5\$

\$\\sum\\limits_i=1^n\\sum\\limits_j=1^m\\gcd(i,j) =\\sum\\limits_i=1^n\\sum\\limits_j=1^m\\sum\\limits_d\\mid i,d\\mid j\\varphi(d) =\\sum\\limits_d=1^N\\varphi(d)(n/d)(m/d)\$

约数个数函数

若\$n=\\prod_i=1^kp_i^a_i\$,则:

\\[d(n)=\\prod_i=1^k(a_i+1) \\]

当\$n\$为素数时，根据定义有\$d(n)=2\$

设\$p_1\$是\$n\$的最小质因子,\$n\'=\\fracnp_1\$

当\$n\'\\bmod p_1=0\$,即\$a_1\\gt 1\$时,设\$last\$为\$n\'\$中\$p_1\$的质数,由约数个数公式可知:
\\[d(n)=d(n\')\\times\\fraclast+2last+1 \\]
当\$n\'\\bmod p_1\\neq 0\$,即\$a_1=1\$时,\$n\'\$与\$p_1\$互质,而约数个数函数是积性函数，故：
\\[\\beginaligned d(n)&=d(p_1)\\times d(n\') \\\\ &=2d(n\') \\endaligned \\]

const int maxn=1000005;

int vst[maxn],Prime[maxn],cnt=0; //prime
int d[maxn],Min_Divnum[maxn]; //divisors

void Divisors_Number_Table(int n) 
    for(int i=2; i<=n; i++) 
        if(!vst[i]) 
            Prime[++cnt]=i;
            Min_Divnum[i]=1;
            d[i]=2;
        
        for(int j=1; j<=cnt&&i*Prime[j]<=n; j++) 
            vst[i*Prime[j]]=1;
            if(i%Prime[j]==0) 
                Min_Divnum[i*Prime[j]]=Min_Divnum[i]+1;
                d[i*Prime[j]]=d[i]/(Min_Divnum[i]+1)*(Min_Divnum[i]+2);
                break;
            
            Min_Divnum[i*Prime[j]]=1;
            d[i*Prime[j]]=d[i]*d[Prime[j]];

约数和函数

若\$n=\\prod_i=1^kp_i^a_i\$,则:

\\[\\beginaligned \\sigma(n)&=(1+p_1+p_1^2+\\cdots+p_1^a_1)\\times(1+p_2+p_2^2+\\cdots+p_2^a_2)\\times\\cdots\\times(1+p_k+p_k^2+\\cdots+p_k^a_k) \\\\ &=\\prod_i=1^k\\sum_j=0^a_ip_i^j \\endaligned \\]

当\$n\$为素数时，根据定义有\$\\sigma(n)=n+1\$

设\$p_1\$是\$n\$的最小质因子,\$n\'=\\fracnp_1\$

当\$n\'\\bmod p_1=0\$,即\$a_1\\gt 1\$时,设\$last=p^a_1-1_1\$也就是\$n\'\$中\$p_1\$为底的最后一个幂，设\$sum=\\sum^a_1-1_i=0p^i_1\$,由约数个数公式可知：
\\[\\sigma(n)=\\sigma(n\')\\times \\fracsum+lastsum \\]
当\$n\'\\bmod p_1\\neq 0\$,即\$a_1=1\$时,\$n\'\$与\$p_1\$互质,而约数个数函数是积性函数，故：
\\[\\beginaligned \\sigma(n)=\\sigma(p_1)\\times \\sigma(n\')\\\\ =(p_1+1)\\sigma(n\') \\endaligned \\]

typedef long long LL;
const int maxn=1000005;
int vst[maxn],Prime[maxn],cnt=0; //prime
LL f[maxn],Min_Fac_last[maxn],Min_Fac_sum[maxn]; //divisors
void Divisors_Sum_Table(int n) 
    f[1]=1;
    for(int i=2; i<=n; i++) 
        if(!vst[i]) 
            Prime[++cnt]=i;
            Min_Fac_last[i]=i;
            f[i]=Min_Fac_sum[i]=i+1;
        
        for(int j=1; j<=cnt&&i*Prime[j]<=n; j++) 
            vst[i*Prime[j]]=1;
            if(i%Prime[j]==0) 
                Min_Fac_last[i*Prime[j]]=Min_Fac_last[i]*Prime[j];
                Min_Fac_sum[i*Prime[j]]=Min_Fac_sum[i]+Min_Fac_last[i*Prime[j]];
                f[i*Prime[j]]=f[i]/Min_Fac_sum[i]*Min_Fac_sum[i*Prime[j]];
                break;
            
            f[i*Prime[j]]=f[i]*(Prime[j]+1);
            Min_Fac_last[i*Prime[j]]=Prime[j];
            Min_Fac_sum[i*Prime[j]]=Prime[j]+1;