基于LSTM网络的视觉识别matlab仿真
Posted matlabfpga
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于LSTM网络的视觉识别matlab仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
随着计算机技术的快速发展,视觉识别技术在越来越多的领域得到应用,比如机器人领域,海底探测领域,安全识别领域等[01,02]。在这些应用领域中,视觉识别系统的准确性以及实时性直接对整个系统的性能有着深远的影响。目前为止,视觉识别系统涉及到包括计算机科学,图像处理技术,神经网络技术,模式识别技术,信号处理与分析技术以及认知学等多种科学技术。视觉识别技术是一种通过视觉传感器采集客观环境中的图像,并通过图像处理技术对采集得到的图像进行处理,分析并进行识别,从而为系统提供一个可进行分析的图像分析结果。
到目前为止,视觉识别技术已经在如下几个领域有了较为广泛的应用:
第一、工业检测方面:视觉识别在工业检测领域,通过计算机进行自动化的视觉识别,可以最大程度的提高工业品的质量,并提升工业品的生产效率。
第二、医学图像检测方面:视觉识别在医学图像检测领域,可以协助医生进行医学图像的技术分析,识别出细小的病变组织。医学图像的视觉识别,涉及到图像处理技术,图像识别技术以及医学影像分析等多个技术,因此通过计算机的视觉识别可以提高医生对病变组织判断的准确率。
第三、安保、监控方面:视觉识别在安保、监控领域,可以提高用户的身份鉴别的准确率,跟踪可疑人员从而减少危险事故的发生。安保、监控领域,目前应用较为常见的有交通管理系统,银行安全系统等多个方面。
RNN,Recurrent Neural Network,即递归神经网络,其基本结构如下图所示: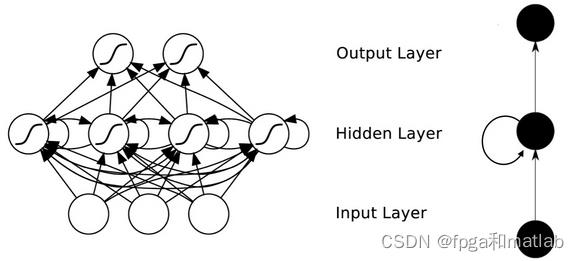
从图的递归神经网络结构可知,将传统的前馈神经网络以循环的方法进行连接,便可以得到递归神经网络。RNN在每一次反馈的时候会存在一定程度的信息损失,当累积到一定程度的时候,就会导致RNN神经网络丧失长时间记忆的能力。鉴于这个缺陷,长短时记忆模型LSTM将解决这个问题。
长短时记忆模型LSTM是由Hochreite等人在1997年首次提出的,其主要原理是通过一种特殊的神经元结构用来长时间存储信息。LSTM网络模型的基本结构如下图所示: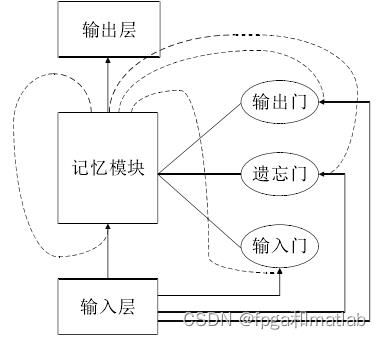
从图的结构图可知,LSMT网络结构包括输入层,记忆模块以及输出层三个部分,其中记忆模块由输入门(Input Gate)、遗忘门(Forget Gate)以及输出门(Output Gate)。LSTM模型通过这三个控制门来控制神经网络中所有的神经元的读写操作。
LSTM模型的基本原理是通过多个控制门来抑制RNN神经网络梯度消失的缺陷。通过LSTM模型可以在较长的时间内保存梯度信息,延长信号的处理时间,因此LSTM模型适合处理各种频率大小的信号以及高低频混合信号。LSTM模型中的记忆单元中输入门(Input Gate)、遗忘门(Forget Gate)以及输出门(Output Gate)通过控制单元组成非线性求和单元。其中输入门、遗忘门以及输出门三个控制门的激活函数为Sigmoid函数,通过该函数实现控制门“开”和“关”状态的改变。
下图为LSTM模型中记忆模块的内部结构图: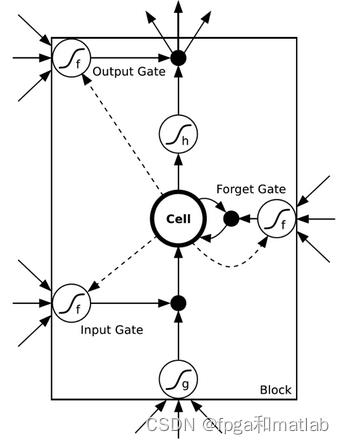
从图的结构图可知,LSTM的记忆单元的工作原理为,当输入门进入”开“状态,那么外部信息由记忆单元读取信息,当输入门进入“关”状态,那么外部信息无法进入记忆单元。同理,遗忘门和输出门也有着相似的控制功能。LSTM模型通过这三个控制门将各种梯度信息长久的保存在记忆单元中。当记忆单元进行信息的长时间保存的时候,其遗忘门处于“开”状态,输入门处于“关”状态。
当输入门进入“开”状态之后,记忆单元开始接受到外部信息并进行存储。当输入门进入“关”状态之后,记忆单元暂停接受外部信息,同时,输出门进入“开”状态,记忆单元中保存的信息传输到后一层。而遗忘门的功能则是在必要的时候对神经元的状态进行重置。
二、核心程序
function nn = func_LSTM(train_x,train_y,test_x,test_y);
binary_dim = 8;
largest_number = 2^binary_dim - 1;
binary = cell(largest_number, 1);
for i = 1:largest_number + 1
binaryi = dec2bin(i-1, binary_dim);
int2binaryi = binaryi;
end
%input variables
alpha = 0.000001;
input_dim = 2;
hidden_dim = 32;
output_dim = 1;
%initialize neural network weights
%in_gate = sigmoid(X(t) * U_i + H(t-1) * W_i)
U_i = 2 * rand(input_dim, hidden_dim) - 1;
W_i = 2 * rand(hidden_dim, hidden_dim) - 1;
U_i_update = zeros(size(U_i));
W_i_update = zeros(size(W_i));
%forget_gate = sigmoid(X(t) * U_f + H(t-1) * W_f)
U_f = 2 * rand(input_dim, hidden_dim) - 1;
W_f = 2 * rand(hidden_dim, hidden_dim) - 1;
U_f_update = zeros(size(U_f));
W_f_update = zeros(size(W_f));
%out_gate = sigmoid(X(t) * U_o + H(t-1) * W_o)
U_o = 2 * rand(input_dim, hidden_dim) - 1;
W_o = 2 * rand(hidden_dim, hidden_dim) - 1;
U_o_update = zeros(size(U_o));
W_o_update = zeros(size(W_o));
%g_gate = tanh(X(t) * U_g + H(t-1) * W_g)
U_g = 2 * rand(input_dim, hidden_dim) - 1;
W_g = 2 * rand(hidden_dim, hidden_dim) - 1;
U_g_update = zeros(size(U_g));
W_g_update = zeros(size(W_g));
out_para = 2 * zeros(hidden_dim, output_dim) ;
out_para_update = zeros(size(out_para));
% C(t) = C(t-1) .* forget_gate + g_gate .* in_gate
% S(t) = tanh(C(t)) .* out_gate
% Out = sigmoid(S(t) * out_para)
%train
iter = 9999; % training iterations
for j = 1:iter
% generate a simple addition problem (a + b = c)
a_int = randi(round(largest_number/2)); % int version
a = int2binarya_int+1; % binary encoding
b_int = randi(floor(largest_number/2)); % int version
b = int2binaryb_int+1; % binary encoding
% true answer
c_int = a_int + b_int; % int version
c = int2binaryc_int+1; % binary encoding
% where we\'ll store our best guess (binary encoded)
d = zeros(size(c));
% total error
overallError = 0;
% difference in output layer, i.e., (target - out)
output_deltas = [];
% values of hidden layer, i.e., S(t)
hidden_layer_values = [];
cell_gate_values = [];
% initialize S(0) as a zero-vector
hidden_layer_values = [hidden_layer_values; zeros(1, hidden_dim)];
cell_gate_values = [cell_gate_values; zeros(1, hidden_dim)];
% initialize memory gate
% hidden layer
H = [];
H = [H; zeros(1, hidden_dim)];
% cell gate
C = [];
C = [C; zeros(1, hidden_dim)];
% in gate
I = [];
% forget gate
F = [];
% out gate
O = [];
% g gate
G = [];
% start to process a sequence, i.e., a forward pass
% Note: the output of a LSTM cell is the hidden_layer, and you need to
for position = 0:binary_dim-1
% X ------> input, size: 1 x input_dim
X = [a(binary_dim - position)-\'0\' b(binary_dim - position)-\'0\'];
% y ------> label, size: 1 x output_dim
y = [c(binary_dim - position)-\'0\']\';
% use equations (1)-(7) in a forward pass. here we do not use bias
in_gate = sigmoid(X * U_i + H(end, :) * W_i); % equation (1)
forget_gate = sigmoid(X * U_f + H(end, :) * W_f); % equation (2)
out_gate = sigmoid(X * U_o + H(end, :) * W_o); % equation (3)
g_gate = tanh(X * U_g + H(end, :) * W_g); % equation (4)
C_t = C(end, :) .* forget_gate + g_gate .* in_gate; % equation (5)
H_t = tanh(C_t) .* out_gate; % equation (6)
% store these memory gates
I = [I; in_gate];
F = [F; forget_gate];
O = [O; out_gate];
G = [G; g_gate];
C = [C; C_t];
H = [H; H_t];
% compute predict output
pred_out = sigmoid(H_t * out_para);
% compute error in output layer
output_error = y - pred_out;
% compute difference in output layer using derivative
% output_diff = output_error * sigmoid_output_to_derivative(pred_out);
output_deltas = [output_deltas; output_error];
% compute total error
overallError = overallError + abs(output_error(1));
% decode estimate so we can print it out
d(binary_dim - position) = round(pred_out);
end
% from the last LSTM cell, you need a initial hidden layer difference
future_H_diff = zeros(1, hidden_dim);
% stare back-propagation, i.e., a backward pass
% the goal is to compute differences and use them to update weights
% start from the last LSTM cell
for position = 0:binary_dim-1
X = [a(position+1)-\'0\' b(position+1)-\'0\'];
% hidden layer
H_t = H(end-position, :); % H(t)
% previous hidden layer
H_t_1 = H(end-position-1, :); % H(t-1)
C_t = C(end-position, :); % C(t)
C_t_1 = C(end-position-1, :); % C(t-1)
O_t = O(end-position, :);
F_t = F(end-position, :);
G_t = G(end-position, :);
I_t = I(end-position, :);
% output layer difference
output_diff = output_deltas(end-position, :);
% H_t_diff = (future_H_diff * (W_i\' + W_o\' + W_f\' + W_g\') + output_diff * out_para\') ...
% .* sigmoid_output_to_derivative(H_t);
% H_t_diff = output_diff * (out_para\') .* sigmoid_output_to_derivative(H_t);
H_t_diff = output_diff * (out_para\') .* sigmoid_output_to_derivative(H_t);
% out_para_diff = output_diff * (H_t) * sigmoid_output_to_derivative(out_para);
out_para_diff = (H_t\') * output_diff;
% out_gate diference
O_t_diff = H_t_diff .* tanh(C_t) .* sigmoid_output_to_derivative(O_t);
% C_t difference
C_t_diff = H_t_diff .* O_t .* tan_h_output_to_derivative(C_t);
% forget_gate_diffeence
F_t_diff = C_t_diff .* C_t_1 .* sigmoid_output_to_derivative(F_t);
% in_gate difference
I_t_diff = C_t_diff .* G_t .* sigmoid_output_to_derivative(I_t);
% g_gate difference
G_t_diff = C_t_diff .* I_t .* tan_h_output_to_derivative(G_t);
% differences of U_i and W_i
U_i_diff = X\' * I_t_diff .* sigmoid_output_to_derivative(U_i);
W_i_diff = (H_t_1)\' * I_t_diff .* sigmoid_output_to_derivative(W_i);
% differences of U_o and W_o
U_o_diff = X\' * O_t_diff .* sigmoid_output_to_derivative(U_o);
W_o_diff = (H_t_1)\' * O_t_diff .* sigmoid_output_to_derivative(W_o);
% differences of U_o and W_o
U_f_diff = X\' * F_t_diff .* sigmoid_output_to_derivative(U_f);
W_f_diff = (H_t_1)\' * F_t_diff .* sigmoid_output_to_derivative(W_f);
% differences of U_o and W_o
U_g_diff = X\' * G_t_diff .* tan_h_output_to_derivative(U_g);
W_g_diff = (H_t_1)\' * G_t_diff .* tan_h_output_to_derivative(W_g);
% update
U_i_update = U_i_update + U_i_diff;
W_i_update = W_i_update + W_i_diff;
U_o_update = U_o_update + U_o_diff;
W_o_update = W_o_update + W_o_diff;
U_f_update = U_f_update + U_f_diff;
W_f_update = W_f_update + W_f_diff;
U_g_update = U_g_update + U_g_diff;
W_g_update = W_g_update + W_g_diff;
out_para_update = out_para_update + out_para_diff;
end
U_i = U_i + U_i_update * alpha;
W_i = W_i + W_i_update * alpha;
U_o = U_o + U_o_update * alpha;
W_o = W_o + W_o_update * alpha;
U_f = U_f + U_f_update * alpha;
W_f = W_f + W_f_update * alpha;
U_g = U_g + U_g_update * alpha;
W_g = W_g + W_g_update * alpha;
out_para = out_para + out_para_update * alpha;
U_i_update = U_i_update * 0;
W_i_update = W_i_update * 0;
U_o_update = U_o_update * 0;
W_o_update = W_o_update * 0;
U_f_update = U_f_update * 0;
W_f_update = W_f_update * 0;
U_g_update = U_g_update * 0;
W_g_update = W_g_update * 0;
out_para_update = out_para_update * 0;
end
nn = newgrnn(train_x\',train_y(:,1)\',mean(mean(abs(out_para)))/2);
mama05-40
三、仿真结论
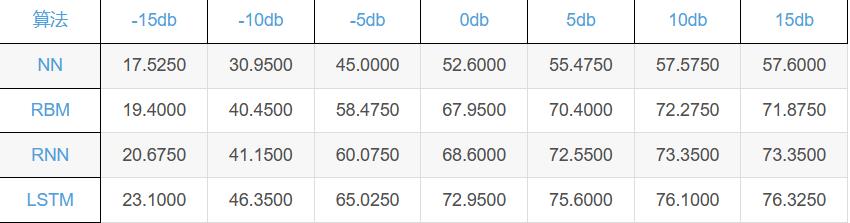
通过本文的LSTM网络识别算法,对不同干扰大小采集得到的人脸进行识别,其识别正确率曲线如下图所示:
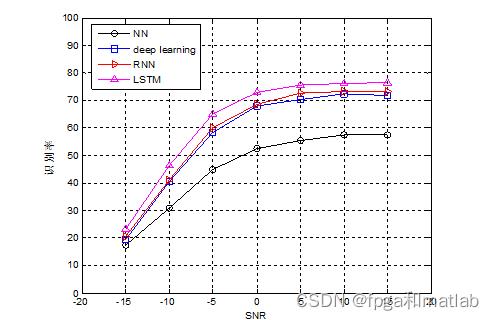
以上是关于基于LSTM网络的视觉识别matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章