『Python』高阶特性

Posted 2020-09-25

python高级特性

1、集合的推导式

• 列表推导式，使用一句表达式构造一个新列表，可包含过滤、转换等操作。

语法：[exp for item in collection if codition]

 

• 字典推导式，使用一句表达式构造一个新列表，可包含过滤、转换等操作。

语法：{key_exp：value_exp for item in collection if codition}

• 集合推导式

语法：{exp for item in collection if codition}

• 嵌套列表推导式

 

2、匿名函数lambda

• 没有函数名
• 单条语句组成
• 语句执行的结果就是返回值
• 可用作sort的key函数

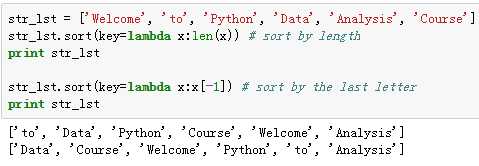
python高阶函数

 

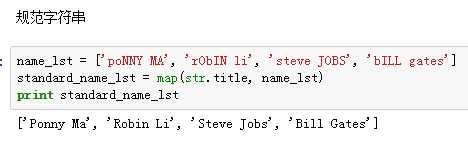
1、map/reduce函数

 

• map(fun, lst)，将传入的函数变量func作用到lst变量的每个元素中，并将结果组成新的列表返回

 

 

 

• reduce（func（x,y），lst），其中func必须有两个参数。每次func计算的结果继续和序列的下一个元素做累积计算。

 

　　lst = [a1, a2 ,a3, ......, an]

 

　　reduce(func(x,y), lst) = func(func(func(a1, a2), a3), ......, an)

 

 

2、filter函数

 

• 筛选序列
• filter（func, lst），将func作用于lst的每个元素，然后根据返回值是True或False判断是保留还是丢弃该元素。

 

 numpy高级函数

1、np.nditer()：numpy迭代器

默认情况下，nditer将视待迭代遍历的数组为只读对象（read-only），为了在遍历数组的同时，实现对数组元素值得修改，必须指定op_flags=[‘readwrite‘]模式：

np.nditer(a, op_flags=[‘readwrite‘])

 

基本迭代参数flag=[‘f_index‘/‘mulit_index‘]，可输出自身坐标it.index/it.multi_index：

a = np.arange(6).reshape(2,3)

‘‘‘迭代方式‘‘‘

# 单维迭代
it = np.nditer(a, flags=[‘f_index‘])
while not it.finished:
    print("%d <%s>" % (it[0], it.index))
    it.iternext()
    
#0 <0>
#1 <2>
#2 <4>
#3 <1>
#4 <3>
#5 <5>


# 多维迭代
it = np.nditer(a, flags=[‘multi_index‘])
while not it.finished:
    print("%d <%s>" % (it[0], it.multi_index))
    it.iternext()
    
#0 <(0, 0)>
#1 <(0, 1)>
#2 <(0, 2)>
#3 <(1, 0)>
#4 <(1, 1)>
#5 <(1, 2)>

 

 改变迭代的顺序：

# 列顺序迭代
it = np.nditer(a, flags=[‘f_index‘], order=‘F‘)
while not it.finished:
    print("%d <%s>" % (it[0], it.index), end=‘ | ‘)
    it.iternext()
    
# 0 <0> | 3 <1> | 1 <2> | 4 <3> | 2 <4> | 5 <5> | 


# 行顺序迭代
it = np.nditer(a, flags=[‘f_index‘], order=‘C‘)
while not it.finished:
    print("%d <%s>" % (it[0], it.index), end=‘ | ‘)
    it.iternext()
    
# 0 <0> | 1 <2> | 2 <4> | 3 <1> | 4 <3> | 5 <5> | 

 

2、ufunc运算

ufunc是universal function的缩写，它是一种能对数组的每个元素进行操作的函数。NumPy内置的许多ufunc函数都是在C语言级别实现的，因此它们的计算速度非常快。

通过组合标准的ufunc函数的调用，可以实现各种算式的数组计算。不过有些时候这种算式不易编写，而针对每个元素的计算函数却很容易用Python实现，这时可以用frompyfunc函数将一个计算单个元素的函数转换成ufunc函数。这样就可以方便地用所产生的ufunc函数对数组进行计算了。让我们来看一个例子。

我们想用一个分段函数描述三角波，三角波的样子如下图所示：

三角波可以用分段函数进行计算

我们很容易根据上图所示写出如下的计算三角波某点y坐标的函数:

def triangle_wave(x, c, c0, hc):
    x = x - int(x) # 三角波的周期为1，因此只取x坐标的小数部分进行计算
    if x >= c: r = 0.0
    elif x < c0: r = x / c0 * hc
    else: r = (c-x) / (c-c0) * hc
    return r

 

显然triangle_wave函数只能计算单个数值，不能对数组直接进行处理。我们可以用下面的方法先使用列表包容(List comprehension)，计算出一个list，然后用array函数将列表转换为数组：

x = np.linspace(0, 2, 1000)
y = np.array([triangle_wave(t, 0.6, 0.4, 1.0) for t in x])

 

这种做法每次都需要使用列表包容语法调用函数，对于多维数组是很麻烦的。让我们来看看如何用frompyfunc函数来解决这个问题：

triangle_ufunc = np.frompyfunc( lambda x: triangle_wave(x, 0.6, 0.4, 1.0), 1, 1)
y2 = triangle_ufunc(x)

 

frompyfunc的调用格式为frompyfunc(func, nin, nout)，其中func是计算单个元素的函数，nin是此函数的输入参数的个数，nout是此函数的返回值的个数。虽然triangle_wave函数有4个参数，但是由于后三个c, c0, hc在整个计算中值都是固定的，因此所产生的ufunc函数其实只有一个参数。为了满足这个条件，我们用一个lambda函数对triangle_wave的参数进行一次包装。这样传入frompyfunc的函数就只有一个参数了。这样子做，效率并不是太高，另外还有一种方法：

def triangle_func(c, c0, hc):
    def trifunc(x):
        x = x - int(x) # 三角波的周期为1，因此只取x坐标的小数部分进行计算
        if x >= c: r = 0.0
        elif x < c0: r = x / c0 * hc
        else: r = (c-x) / (c-c0) * hc
        return r

    # 用trifunc函数创建一个ufunc函数，可以直接对数组进行计算, 不过通过此函数
    # 计算得到的是一个Object数组，需要进行类型转换
    return np.frompyfunc(trifunc, 1, 1)

y2 = triangle_func(0.6, 0.4, 1.0)(x)

 

我们通过函数triangle_func包装三角波的三个参数，在其内部定义一个计算三角波的函数trifunc，trifunc函数在调用时会采用triangle_func的参数进行计算。最后triangle_func返回用frompyfunc转换结果。

值得注意的是用frompyfunc得到的函数计算出的数组元素的类型为object，因为frompyfunc函数无法保证Python函数返回的数据类型都完全一致。因此还需要再次 y2.astype(np.float64)将其转换为双精度浮点数组。