数学知识3.2-卡特兰数

Posted 2023-03-19 Cocoicobird

一、卡特兰数

卡特兰数：\\(C_2n^n-C_2n^n+1=\\fracC_2n^nn+1\\)。

卡特兰数满足递推公式：设 \\(C_n=\\fracC_2n^nn+1\\)，\\(C_1=1\\)，\\(C_n=C_n-1\\frac4n-2n+1\\)。

模板题[AcWing889.满足条件的01序列]

题目描述

给定 \\(n\\) 个 \\(0\\) 和 \\(n\\) 个 \\(1\\)，它们将按照某种顺序排成长度为 \\(2n\\) 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 \\(0\\) 的个数都不少于 \\(1\\) 的个数的序列有多少个。

输出的答案对 \\(10^9+7\\) 取模。

输入格式

共一行，包含整数 \\(n\\)。

输出格式

共一行，包含一个整数，表示答案。

数据范围

\\(1≤n≤10^5\\)

输入样例

3

输出样例

5

解题思路

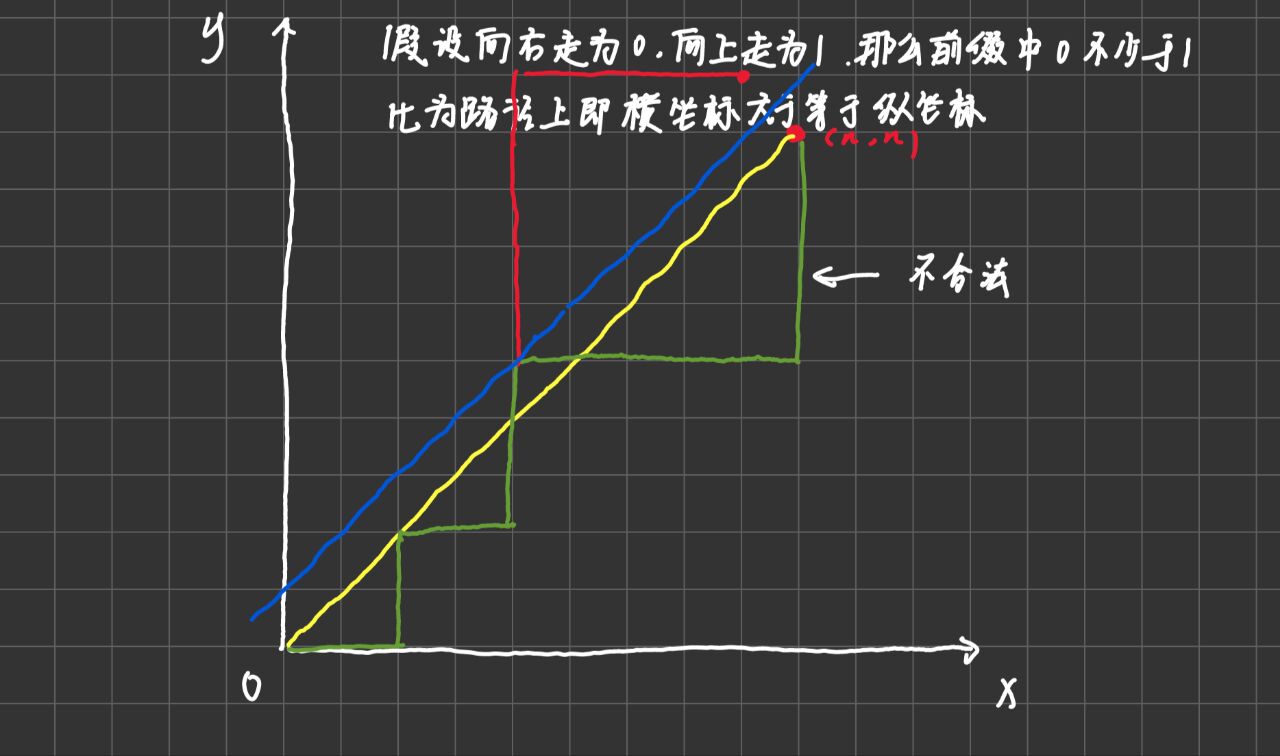
可以看出，每条不合法的路线经过对称都对应着从原点走到 \\((n-1,n+1)\\) 的一条路径，那么所有方案减去不合法方案即是答案。

C++代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, MOD = 1e9 + 7;
typedef long long LL;

int n;

int qmi(int a, int b, int p)

    int res = 1;
    while (b)
    
        if (b & 1) res = (LL) res * a % p;
        a = (LL) a * a % p;
        b >>= 1;
    
    return res;


int main()

    cin >> n;
    int a = 2 * n, b = n;
    int res = 1;
    for (int i = a; i > a - b; i --) res = (LL) res * i % MOD;
    for (int i = b; i > 0; i --) res = (LL) res * qmi(i, MOD - 2, MOD) % MOD;
    res = (LL) res * qmi(n + 1, MOD - 2, MOD) % MOD;
    cout << res;
    return 0;

本文来自博客园，作者：Cocoicobird，转载请注明原文链接：https://www.cnblogs.com/Cocoicobird/p/17234249.html