python的递归算法学习：具体实现：斐波那契和其中的陷阱

Posted 2020-09-23

1.斐波那契

  什么是斐波那契，斐波那契额就是一个序列的整数的排序，其定义如下；

Fn = Fn-1 + Fn-2 
with F0 = 0 and F1 = 1 

也就是，0，1，1，2，3，5，8，13.。。。。

递归实现：

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)

非递归实现：

def fibi(n):
    a, b = 0, 1
    for i in range(n):
        a, b = b, a + b
    return a

在这里，我们如果仔细调试，会发现，递归实现，会消耗更多的时间，这里测试如下：

from timeit import Timer
from fibo import fib

t1 = Timer("fib(10)","from fibo import fib")

for i in range(1,41):
    s = "fib(" + str(i) + ")"
    t1 = Timer(s,"from fibo import fib")
    time1 = t1.timeit(3)
    s = "fibi(" + str(i) + ")"
    t2 = Timer(s,"from fibo import fibi")
    time2 = t2.timeit(3)
    print("n=%2d, fib: %8.6f, fibi:  %7.6f, percent: %10.2f" % (i, time1, time2, time1/time2))

结果如下；

C:\\Python35\\python.exe C:\\pylearn\\bottlelearn\\fibnaqie.py
n= 1, fib: 0.000002, fibi:  0.000003, percent:       0.55
n= 2, fib: 0.000002, fibi:  0.000003, percent:       0.73
n= 3, fib: 0.000003, fibi:  0.000003, percent:       1.20
n= 4, fib: 0.000005, fibi:  0.000003, percent:       1.80
n= 5, fib: 0.000007, fibi:  0.000003, percent:       2.45
n= 6, fib: 0.000012, fibi:  0.000004, percent:       3.31
n= 7, fib: 0.000022, fibi:  0.000003, percent:       6.50
n= 8, fib: 0.000030, fibi:  0.000004, percent:       8.38
n= 9, fib: 0.000049, fibi:  0.000003, percent:      14.58
n=10, fib: 0.000078, fibi:  0.000004, percent:      20.07
n=11, fib: 0.000126, fibi:  0.000004, percent:      35.00
n=12, fib: 0.000203, fibi:  0.000004, percent:      52.29
n=13, fib: 0.000330, fibi:  0.000004, percent:      79.20
n=14, fib: 0.000537, fibi:  0.000004, percent:     120.94
n=15, fib: 0.000925, fibi:  0.000005, percent:     196.18
n=16, fib: 0.001693, fibi:  0.000007, percent:     244.16
n=17, fib: 0.007242, fibi:  0.000011, percent:     652.70
n=18, fib: 0.004422, fibi:  0.000007, percent:     637.64
n=19, fib: 0.010322, fibi:  0.000008, percent:    1240.40
n=20, fib: 0.010813, fibi:  0.000007, percent:    1443.78
n=21, fib: 0.025547, fibi:  0.000011, percent:    2246.24
n=22, fib: 0.035421, fibi:  0.000011, percent:    3192.22
n=23, fib: 0.060877, fibi:  0.000008, percent:    7837.86
n=24, fib: 0.090561, fibi:  0.000007, percent:   12091.41
n=25, fib: 0.132058, fibi:  0.000008, percent:   16415.97
n=26, fib: 0.227813, fibi:  0.000008, percent:   29330.54
n=27, fib: 0.557644, fibi:  0.000014, percent:   38659.17
n=28, fib: 0.578976, fibi:  0.000009, percent:   65224.25
n=29, fib: 1.133326, fibi:  0.000008, percent:  140882.03
n=30, fib: 1.454107, fibi:  0.000009, percent:  169095.94
n=31, fib: 2.274395, fibi:  0.000009, percent:  264486.10
n=32, fib: 3.817956, fibi:  0.000009, percent:  430110.09
n=33, fib: 5.923710, fibi:  0.000009, percent:  688859.58
n=34, fib: 9.629423, fibi:  0.000009, percent: 1020986.44
n=35, fib: 15.910085, fibi:  0.000009, percent: 1686911.18
n=36, fib: 26.556680, fibi:  0.000009, percent: 2901071.88
n=37, fib: 43.014073, fibi:  0.000016, percent: 2673506.31

为什么会这样呢？我们思考一下，递归过程的计算数，具体如下；

 

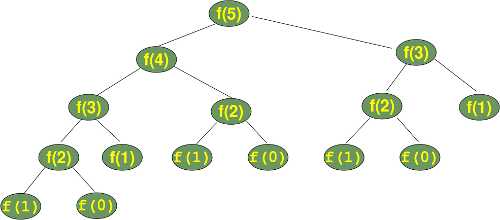
从树中可以看到，有重复计算的情况,(f(1)就计算了很多次。

在这里，尝试做一个改进，引入一个临时的字典，把计算过的内容做一个保存：

memo = {0:0, 1:1}
def fibm(n):
    if not n in memo:
        memo[n] = fibm(n-1) + fibm(n-2)
    return memo[n]

 

重新进行时间的测试：

from timeit import Timer
from fibo import fib

t1 = Timer("fib(10)","from fibo import fib")

for i in range(1,41):
    s = "fibm(" + str(i) + ")"
    t1 = Timer(s,"from fibo import fibm")
    time1 = t1.timeit(3)
    s = "fibi(" + str(i) + ")"
    t2 = Timer(s,"from fibo import fibi")
    time2 = t2.timeit(3)
    print("n=%2d, fib: %8.6f, fibi:  %7.6f, percent: %10.2f" % (i, time1, time2, time1/time2))

n= 1, fib: 0.000011, fibi:  0.000015, percent:       0.73
n= 2, fib: 0.000011, fibi:  0.000013, percent:       0.85
n= 3, fib: 0.000012, fibi:  0.000014, percent:       0.86
n= 4, fib: 0.000012, fibi:  0.000015, percent:       0.79
n= 5, fib: 0.000012, fibi:  0.000016, percent:       0.75
n= 6, fib: 0.000011, fibi:  0.000017, percent:       0.65
n= 7, fib: 0.000012, fibi:  0.000017, percent:       0.72
n= 8, fib: 0.000011, fibi:  0.000018, percent:       0.61
n= 9, fib: 0.000011, fibi:  0.000018, percent:       0.61
n=10, fib: 0.000010, fibi:  0.000020, percent:       0.50
n=11, fib: 0.000011, fibi:  0.000020, percent:       0.55
n=12, fib: 0.000004, fibi:  0.000007, percent:       0.59
n=13, fib: 0.000004, fibi:  0.000007, percent:       0.57
n=14, fib: 0.000004, fibi:  0.000008, percent:       0.52
n=15, fib: 0.000004, fibi:  0.000008, percent:       0.50
n=16, fib: 0.000003, fibi:  0.000008, percent:       0.39
n=17, fib: 0.000004, fibi:  0.000009, percent:       0.45
n=18, fib: 0.000004, fibi:  0.000009, percent:       0.45
n=19, fib: 0.000004, fibi:  0.000009, percent:       0.45
n=20, fib: 0.000003, fibi:  0.000010, percent:       0.29
n=21, fib: 0.000004, fibi:  0.000009, percent:       0.45
n=22, fib: 0.000004, fibi:  0.000010, percent:       0.40
n=23, fib: 0.000004, fibi:  0.000010, percent:       0.40
n=24, fib: 0.000004, fibi:  0.000011, percent:       0.35
n=25, fib: 0.000004, fibi:  0.000012, percent:       0.33
n=26, fib: 0.000004, fibi:  0.000011, percent:       0.34
n=27, fib: 0.000004, fibi:  0.000011, percent:       0.35
n=28, fib: 0.000004, fibi:  0.000012, percent:       0.32
n=29, fib: 0.000004, fibi:  0.000012, percent:       0.33
n=30, fib: 0.000004, fibi:  0.000013, percent:       0.31
n=31, fib: 0.000004, fibi:  0.000012, percent:       0.34
n=32, fib: 0.000004, fibi:  0.000012, percent:       0.33
n=33, fib: 0.000004, fibi:  0.000013, percent:       0.30
n=34, fib: 0.000004, fibi:  0.000012, percent:       0.34
n=35, fib: 0.000004, fibi:  0.000013, percent:       0.31
n=36, fib: 0.000004, fibi:  0.000013, percent:       0.31
n=37, fib: 0.000004, fibi:  0.000014, percent:       0.29
n=38, fib: 0.000004, fibi:  0.000014, percent:       0.29
n=39, fib: 0.000004, fibi:  0.000013, percent:       0.31
n=40, fib: 0.000004, fibi:  0.000014, percent:       0.29